
第5卷第3期 智能系统学报 Vol.5 No.3 2010年6月 CAAI Transactions on Intelligent Systems Jun.2010 doi:10.3969/i.issn.1673-4785.2010.03.005 分形图像编码算法的参数选择对算法性能的影响 崔朝辉,刘冀伟,王志良,曲波 (北京科技大学信息工程学院,北京100083) 摘要:实际应用中的分形图像编码算法有众多参数需要确定,参数选择的恰当与否直接影响算法的性能,而如何 确定参数的最佳值是每个研究者和使用者需要首先面对的问题.通过对基本的分形图像编解码算法的分析,发现解 码图像的质量(PSNR)不仅跟值域块的分块大小相关,还跟图像的活跃度(IAM)相关.实验进一步表明,对应每一种 分块大小,PSNR与IAM均存在对数关系;而且在解码过程中,仅需要6次迭代,解码图像就进入稳定状态. 关键词:分形图像编码;图像活跃度量;PSNR估计;参数选择 中图分类号:TP311文献标识码:A文章编号:16734785(2010)03023307 The impact of parameter selection on fractal image coding algorithm performance CUI Zhao-hui,LIU Ji-wei,WANG Zhi-liang,QU Bo (School of Information Engineering,University of Science and Technology Beijing,Beijing 100083,China) Abstract:A number of parameters need to be determined before a fractal image coding algorithm can be used.The performance of the algorithm is directly affected by the selection of parameters.Determining the optimal values is the first problem that each researcher and user faces.Analysis of basic fractal image encoding and decoding algo- rithms showed the quality of a decoded image,as measured by the peak signal-to-noise ratio (PSNR),is not only related to the size of range blocks,but also the Image activity measure (IAM).Experiments showed that,for each range block,the relationship between PSNR and IAM is logarithmic.Moreover,the experiments indicated that only 6 iterations were required in the decoding process before an image went to a steady state. Keywords:fractal image coding;image activity measure(IAM);PSNR estimation;parameter selection 分形图像编码算法是目前研究较为广泛的编码 确定因素:1)原始图像分块大小不好确定,需要通 方法之一,对其研究已有近20年的历史.Bam8- 过逐次实验的方法进行尝试,鉴于该算法的计算量 ley21最早将分形的概念引入到图像压缩编码领 非常大,相对而言这是一项耗时耗力的工作.尽管已 域,但其编码过程需要人工干预;l989年Jacquin34 经有不少研究致力于减少搜索空间,提高运算效率, 提出局部迭代函数系统(partial iterated function sys- 但却是以降低解码图像质量为代价.2)压缩比 tems,PIFS)的概念,实现了分块的自动分形图像编 (CR)和解码图像质量(以峰值信噪比PSNR来衡 码算法,使分形图像编码取得了突破性进展,成为后 量)事先未知,必须在实际的编解码过程结束后,才 人研究和扩展的起点.该算法具有许多优点56:它 能计算出来.3)解码时候的迭代次数不容易决定, 突破以往熵压缩编码的界限,在编码过程中,采用了 一般研究为了保证解码图像进入稳定状态,常常采 类似描述的方法,而解码时通过迭代完成,且具有分 用几十次迭代,白白浪费计算资源,确定有效的迭代 辨率无关的解码特性等.然而,在将分形图像编解码 次数在资源受限的应用场合中变得尤为重要, 算法应用到实践中的时候,该算法表现出太多的不 针对上述3个问题,本文展开算法分析和实验 验证,为将分形图像编解码算法应用在实际中,提供 收稿日期:20090903. 了具有指导意义的结论.根据图像活跃度与图像解 基金项目:国家“863”计划资助项目(2007AA01Z160):北京市重点学 码质量的关系式,可预先给出分块大小的建议值,进 科建设资助项目(XK100080537) 通信作者:崔朝辉.E-mail:zhh.cui@gmail.com 而估计出压缩比;迭代解码过程中,初始图像对稳定

·234 智能系统学报 第5卷 图像没有影响,迭代次数6次以上,图像就进人稳定 提8]:1)自然界中不同种类的形态一般具有不同的 状态. 分形维数;2)Pentland的假设,即自然界中的分形与 1基本编解码算法 图像的灰度表示之间有着一定的对应关系, Mandelbrot于1975年创立了分形几何学,他在 文献[7]给出了基本的分形编解码算法具体步 专著「9中是这样定义分形的:其组成部分与整体以 骤,为了行文连续,特摘录如下: 某种方式相似的形体叫做分形.isher给出了一个 1)对待压缩图像进行分割. 描述性定义[1o:如果一个集合F被视为分形,那 将大小为N×N的原始灰度图像I分割成互不 么认为它应具有以下(部分)特点:1)F在任意尺度 相交的大小为R×R的方块R:(range block,称为值 都存在细节:2)F具有完全的(或部分的、概率的) 域块),即I=UR,且R∩R=0,i≠j,R:是分形压 自相似性;3)F的分形维数大于其拓扑维数;4)F有 缩中的每一个编码单元: 一个简单的算法性描述(FS).所以说,分形维数是 2)建立搜索空间. 表征图像的一个重要参数.它是独立于图像分辨率 用2R×2R的截取窗口沿原图像的水平和垂直 和视角而稳定存在的物质表示量.分形维数把图像 方向(即xy轴)分别以步长△h和△x移动,每一次 的空间信息与灰度信息有机地结合起来,为图像处 移动后的截取方块就构成了匹配块D:(domain 理提供了新的工具 blo©k,称为定义域块),所有这样的匹配块D,就构 分形盒维数(fractional box-counting dimension) 成了搜索空间So 是Feng在博士论文I2中提出的,可以得到比较精 3)寻找最优匹配块 确的维数估计值.它较好地反映了图像灰度变化的 在搜索空间内,对每一值域块R,通过最小均 复杂度,视觉上相似的2个子块,分形盒维数也是近 方误差(mean square error,MSE)原则寻找误差最小 似相等的;反之,分形盒维数相差很大的2个子块, 的匹配块D,使D:经适当的仿射变换:来逼近R, 在视觉上一般是不相似的.由此可见,图像的分形盒 即D,R,使之满足 维数可能是影响算法性能的一个因素, d(R,o(D:)=IR-(s:·(A(G(D))+o:)I2= 从编解码过程可以看出,能影响到算法性能的 mR,-s·(A(G(D,))+:)I2. 因素还有如下几个: 式中:G为固定的几何变换,完成从Domain块到 1)值域块的大小R:值域块分割比较小的时候, 跟定义域块的匹配会比较好,误差比较小;但相应的 Range块的空间压缩映射,通常用四点平均法(2×2 采样);A为8种对称旋转变换之一,:和0:分别是 搜索空间也大,会带来压缩比降低、运算量大的问 题.值域块分割比较大,则效果相反, 灰度变换的尺度因子和偏移因子 4)生成编码. 2)截取步长△h和△:截取步长比较小的时候, 通过搜索得到满足的变换群集ω,(x,y,a,s, 能得到更多的值域块,与定义域块的匹配误差可能 o:)(其中y:表示D:的位置)就构成了PIFS,将 会小,但相应的搜索空间急剧增加,显著增大运算 PIS记录下来并进行量化编码,即得到每个R:的 量.截取步长比较大时,则相反,但目前相关的研究 分形码(fractal codes). 中都是取△h=△v=R,所以这一因素暂不考虑 5)迭代解码. 3)迭代次数:解码过程中,迭代解码次数越多, 以任意灰度图像(与待解码图像尺寸相同)作 恢复图像的质量越好,但一般认为过多的迭代次数 为初始点集,读取PIFS中每一编码块R:对应的仿 并不能带来图像质量的明显上升, 射变换的参数:,按与编码过程中相同的顺序作用 关于压缩比,对于值域块大小R而言,所占存 到初始点集,反复迭代至收敛后,所得到的吸引子就 储空间是R×Rx8(对应8bit/pixel的灰度图像), 是最终的解码图像, 而编码后,需要存储对应D块的坐标值x:和y,占 用空间大小为;对应的a:代表8种变换之一,占用 2分形图像编码算法 空间为B;s:和o:各占用y;这样未经过量化和嫡编 将分形理论应用在图像处理中,有如下2个前 码的压缩比就可以通过式(1)计算出来

第3期 崔朝辉,等:分形图像编码算法的参数选择对算法性能的影响 ·235· R2×8 25525 CR=2x(a+y)×8+B (1) E2=- ∑∑Plbp =0=01 3相关影响因素 3.4分块统计特征 由于值域块R与定义域块D:的匹配过程是在 下面将着重寻找影响恢复图像质量的因素,并 MSE原则下进行的,自然会考虑图像分块的统计特 试图找出影响规律。 征是否会影响到分形编码算法的性能.这里对每种 3.1性能评价指标 分块方式,考虑4种指标:块平均值m的平均值C1、 采用图像编码中常用的峰值信噪比(PSNR)和 块平均值的标准差C2、块标准差σ的平均值C3、块 压缩比(CR)为2个评价指标,考察分形编码算法. 标准差的标准差C4,这里图像块的平均值和标准差 二者的通用计算公式如下: 计算公式如下: CR Sociginal Scoded m PSNR=10×gx 2552×X×Y 0= 1Σ (i》-i0 WR×R-12 1(i)-m)2. 3.5图像活跃度量 式中:S为文件大小,X和Y为图像大小,I(i,)为图 图像活跃度量(image activity measure,.IAM)也 像点(i,)处的像素灰度值.这里所计算的图像为 是一个表达图像灰度活跃程度的度量,其在文献 8bits的灰度图像. [14]中有不同的定义,这里采用如下定义方式[5]: 3.2分形盒维数 X-I Y 采用文献[13]的计算方法.将N×N大小的灰度 IAM x ,1I(i,)-I(i+1,)1+ 图像分制成大小为6×6的子块(1<6≤分8为整数), X Y-1 含名1i》-+1)小 ns(i)是覆盖第(i,j)子块中的图像所需的盒子数,k (k=1,2,…,n)表示第(iJ)子块中的所有n个像素点 4 实验和结果 灰度值,图像的分形盒维数F计算如下: 实验计算机配置为Intel Pentium4D506 ng(i,j)=(max I min I)/6, 2.66 GHz CPU、1 GB DDR RAM,软件采用QT图形 Na=∑n(i), 界面、C++语言编写,实验图像来自USC-SPI图像 In NS 库161,均已调整为512×512×8bits大小的BMP格 F=四-ln8 式灰度图像.在对源图像进行编解码的时候,采用值 3.3一维熵和二维熵 域块R=2,4,8,164种分块方式,相应的C1、C2、C3 图像熵是一个重要的表征图像整体复杂性的 和C4也针对这4种分块方式进行计算,E2的邻域 量,嫡值越高,说明图像越复杂,即附带的信息量越 半径取值为r=1,2,…,5. 大,越难于压缩,或者说,在相同的压缩比下,越难于 图1给出了各种可能的因素对PSNR的影响情 获得高的解码图像质量, 况.图1(a)表明在同一种分块情况下,分形盒维数 令p:(i=0,1,…,255)表示图像中像素值为i 对PSNR几乎不存在有规律影响,大致上可以看出, 的像素点所占比例,一维熵定义为 当分形盒维数变大时,PSNR略有降低.但是,并不 255 能有效地区分出在不同分块情况下,分形盒维数对 E,=-】 pb po PSNR的影响,也即分形盒维数对分块大小的区分 为了反应图像灰度分布的空间特征,选择图像的? 度不够高.图1(b)和图1(c)表明考察的4种统计 邻域灰度均值作为灰度分布的空间特征量,与图像 特征对PSNR也没有影响.图1(d)和图1(e)表明 的像素灰度组成特征二元组,记为(i,),其中i表示 图像的熵对PSNR也没有影响,图1(f)从另一个角 像素的灰度值,j表示i的半径为r的邻域灰度均 度也反映了这一点. 值.令P为(i,)出现的频率,则二维嫡定义为
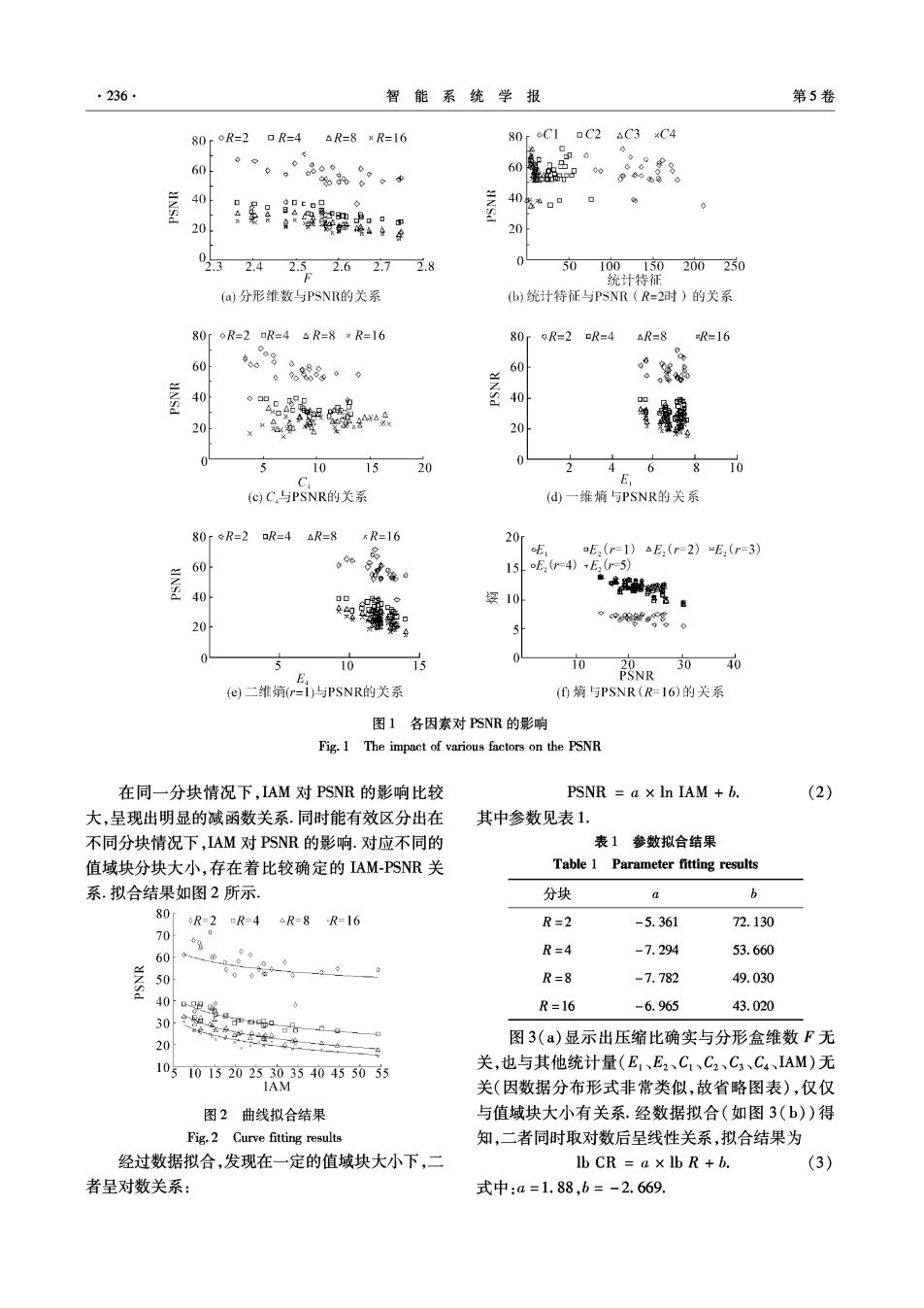
·236 智能系统学报 第5卷 80roR=2口R=4△R=8×R=16 80C1 C2 6C3 xC4 60 。,品 8%8。+ 60 40 400 20 20 2.4 2.52.62.72.8 50100150 200250 统计特征 (a)分形维数与PSNR的关系 b)统计特征与PSNR(R=2时)的关系 80r◇R=2R=4△R=8¥R=16 80rR=2R=4 △R=8 R=16 60 g。 。能品·9 60 NSd 40 40 20 20 5 5 10 15 20 C E 6810 (c)C,与PSNR的关系 (d一维痛与PSNR的关系 80rR=2R=4△R=8KR=16 20r 。8 E E2(r=1)△E,(r=2)E2(r=3) 60 15E,(r4)+E.(r5 40 姿10 #嘴… 20 5 。80 0 15 00 10 20 3040 E PSNR (e)二维熵(r=i)与PSNR的关系 (④熵与PSNR(R=16)的关系 图1各因素对PSNR的影响 Fig.1 The impact of various factors on the PSNR 在同一分块情况下,IAM对PSNR的影响比较 PSNR a x In IAM +b. (2) 大,呈现出明显的减函数关系.同时能有效区分出在 其中参数见表1. 不同分块情况下,IAM对PSNR的影响.对应不同的 表1参数拟合结果 值域块分块大小,存在着比较确定的IAM-PSNR关 Table 1 Parameter fitting results 系.拟合结果如图2所示。 分块 b 80r oR=2R=4△R=8R=16 R=2 -5.361 72.130 70 0 60 R=4 -7.294 53.660 50 R=8 -7.782 49.030 40器4 R=16 -6.965 43.020 30 20 这的中一白 图3(a)显示出压缩比确实与分形盒维数F无 10510152025303540455055 关,也与其他统计量(E,、E2、C1、C2、C3、C4、IAM)无 IAM 关(因数据分布形式非常类似,故省略图表),仅仅 图2曲线拟合结果 与值域块大小有关系.经数据拟合(如图3(b))得 Fig.2 Curve fitting results 知,二者同时取对数后呈线性关系,拟合结果为 经过数据拟合,发现在一定的值域块大小下,二 lbCR=a×lbR+b. (3) 者呈对数关系: 式中:a=1.88,b=-2.669
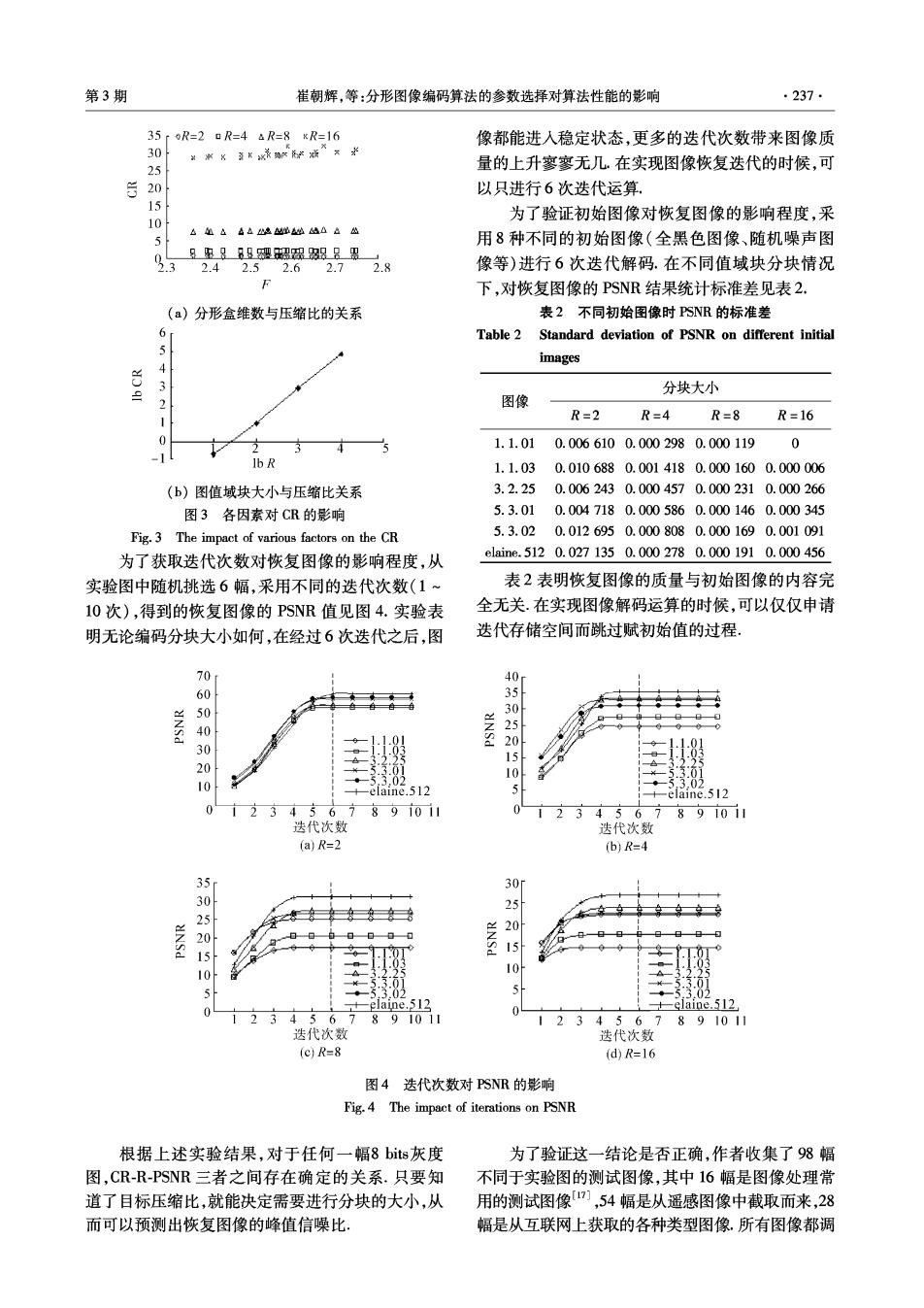
第3期 崔朝辉,等:分形图像编码算法的参数选择对算法性能的影响 237 35r6R=20R=4&R=8xR=16 像都能进人稳定状态,更多的迭代次数带来图像质 30 常8百x杀8m花洁× 25 量的上升寥寥无几.在实现图像恢复迭代的时候,可 S 20 以只进行6次迭代运算. 15 为了验证初始图像对恢复图像的影响程度,采 10 6L&4a4地丛△&△ 用8种不同的初始图像(全黑色图像、随机噪声图 2.3 9恩及89题盟踢盟8聚 2.42.52.62.7 2.8 像等)进行6次迭代解码.在不同值域块分块情况 F 下,对恢复图像的PSNR结果统计标准差见表2. (a)分形盒维数与压缩比的关系 表2不同初始图像时PSNR的标准差 6 Table 2 Standard deviation of PSNR on different initial images 4 分块大小 图像 R=2 R=4 R=8 R=16 1.1.01 0.0066100.0002980.000119 0 IbR 1.1.03 0.0106880.0014180.0001600.000006 (b)图值域块大小与压缩比关系 3.2.25 0.0062430.0004570.0002310.000266 图3各因素对CR的影响 5.3.010.0047180.0005860.0001460.000345 Fig.3 The impact of various factors on the CR 5.3.020.0126950.0008080.0001690.001091 为了获取迭代次数对恢复图像的影响程度,从 elaine.5120.0271350.0002780.0001910.000456 实验图中随机挑选6幅,采用不同的迭代次数(1~ 表2表明恢复图像的质量与初始图像的内容完 10次),得到的恢复图像的PSNR值见图4.实验表 全无关.在实现图像解码运算的时候,可以仅仅申请 明无论编码分块大小如何,在经过6次迭代之后,图 迭代存储空间而跳过赋初始值的过程, 70 40 60 30 % 30 .01 15 3.01 10 o 302 +elaine.512 5 elaine.512 234567 89i1011 34567 891011 迭代次数 迭代次数 (a)R=2 b)R=4 0 2 十 520 15 10 5 205 5 elaine.512 elaine.512 0 2 34567 891011 234567 891011 迭代次数 迭代次数 (c)R=8 (d)R=16 图4迭代次数对PSNR的影响 Fig.4 The impact of iterations on PSNR 根据上述实验结果,对于任何一幅8bits灰度 为了验证这一结论是否正确,作者收集了98幅 图,CR-R-PSNR三者之间存在确定的关系.只要知 不同于实验图的测试图像,其中16幅是图像处理常 道了目标压缩比,就能决定需要进行分块的大小,从 用的测试图像,54幅是从遥感图像中截取而来,28 而可以预测出恢复图像的峰值信噪比 幅是从互联网上获取的各种类型图像.所有图像都调

238. 智能系统学报 第5卷 整为480×480×8bits的BMP格式灰度图像.目标压 1996,24(10):1-7. 缩比是16倍,根据式(3)计算出建议的分块大小为 [7]袁静,冯前进,陈武凡,等.基于小波分解的快速分形 R=11.69,试验中取R=12,并根据式(2)预测出 图象压缩算法[J].中国图象图形学报,2003,8(4): PSNR(a=-7.636,b=46.56).对所有98幅测试图 392-397. 像的预测误差进行分析(见表3).作为比较,同时列 YUAN Jing,FENG Qianjin,CHEN Wufan,et al.A new fast fractal coding approach based on wavelet decomposition 出了R=8,16两种情况.结果表明,上述结论的预测 [J].Joural of Image and Graphics,2003,8(4):392-397. 误差在可接受的范围内,且具有普遍意义,不因图像 [8]何传江,黄娟娟,李高平.基于分数盒维数的快速分形图 内容而改变,也不因图像大小而改变 像编码[J].中国图象图形学报,2007,12(2):27282. 表3测试结果 HE Chuanjiang,HUANG Juanjuan,LI Gaoping.Fast fractal Table 3 Test results image coding based on fractional box-counting dimension[J]. PSNR CR Joumal of Image and Graphics,2007,12(2):277-282. 参数 [9]MANDELBROT BB.The factal gometry of nature M]. R=8R=12R=16 R=8R=12R=16 San Francisco:Freeman,1982:15-16. 平均值1.761.972.190.370.431.35 [10]FISHER Y.Fractal image compression:theory and appli- 标准差1.611.532.571.492.375.56 cation[M].New York:Springer-Verlag,1995:28-29. 5 结束语 [11]曹媛媛,杨波,徐光祐.基于分形纹理特征和小波变换 的网状纹理检测方法[J].自动化学报,2007,33(7): 本文通过对基本分形图像编码算法的详细分析 688692 和测试,发现该算法解码图像的PSNR不仅与值域 CAO Yuanyuan,YANG Bo,XU Guangyou.Netlike tex- 块分块大小有关系,更与IAM密切相关,当分块大 ture detection method using fractal texture features and wavelet transform[J].Acta Automatic Sinica,2007,33 小确定的时候,后二者之间存在对数关系;而压缩比 (7):688692. 却仅仅与值域块分块大小相关,二者在对数下呈线 [12]FENG J.Fractional fractal geometry for image processing 性关系.对任意8bis灰度图像,如果确定了目标压 [D].Evanston,Illinois:Northwestern University,2000. 缩比,就能根据关系式(3)推算应该采用什么样的 [13]于子凡,杜贵君,林宗坚。图像盒子维数特征计算方法 分块方式,同时根据关系式(2)就能推算出解码图 改进[J].测绘科学,2006,31(1):8789. 像的PSNR能达到什么样的水平.在实际应用中,本 YU Zifan,DU Guijun,LIN Zongjian.An improved algo- 文验证了初始图像对迭代解码结果没有影响;不论 rithm of box counting for digital image[J].Science of Sur- 采用什么样的分块方式,只需要6次迭代,就可以得 veying and Mapping,2006,31(1):87-89. 到稳定的恢复图像, [14]SAHA S,VEMURI R.How do image statistics impact lossy coding performance?[C]//Proceedings of Interna- 参考文献: tional Conference on Information Technology:Coding and [1]BARNSLEY M F.Fractal everywhere M].Boston:Aca- Computing.Las Vegas,USA,2000:42-47. [15]CUI Zhaohui,FU Jingliang,LIU Jiwei,et al.What statis- demic Press,1988:375-377. tics is PSNR related using JPEG2000 [C]//2008 IEEE [2]BARNSLEY M F,HURD L P.Fractal image compression Conference on Cybemetics and Intelligent Systems.Cheng- [M].Boston:AK Peters Ltd.,1993:183. d,China,2008:984-989. [3]JACQUIN A G.Fractal image coding:a review J].Pro- [16]USC.The USC-SIPI image database[EB/OL].[2009-08- ceedings of the IEEE,1993,81(10):1211-1225. 01].http://sipi.usc.edu/database/. 4]JACQUIN A G.Image coding based on a fractal theory of it- [17]UTK.The standard test images[EB/OL].[2009-08-01]. erated contractive image transformations[J].IEEE Transac- http://www.ece.utk.edu/~gonzalez/ipweb2e/down- tions on Image Process,1992,1(1):18-30. loads/standard_test_images/standard_test_images.zip. [5]赵耀,王红星,袁宝宗.分形图像编码研究的进展[J]. 作者简介: 电子学报,2000,28(4):95-101. 崔朝辉,男,1983年生,博士研究生 ZHAO Yao,WANG Hongxing,YUAN Baozong.Advances 主要研究方向为图像压缩、图像分析. in fractal image coding[J].Acta Electronica Sinica,2000, 28(4):95-101. [6]温江涛,朱雪龙.基于S分形理论的信源编码技术的 研究[J].电子学报,1996,24(10):1-7. WEN Jiangtao,ZHU Xuelong.A study of IFS fractal based source coding techniques[J].Acta Electronica Sinica

第3期 崔潮辉等:分形图像编码算法的参数选择对算法性能的影响 239 刘冀伟,男,1962年生,副教授、博 王志良,男,1956年生,国家二级教 土,北京科技大学信息工程学院自动化 授、博士生导师、博土,北京科技大学 系副主任,IEEE会员,中国人工智能 电子信息系主任,中国人工智能学会人 学会人工心理与情感计算专业委员 工心理与人工情感专业委员会主任,第 会理事.主要研究方向为图像处理、 一届国际情感计算和智能交互学术大 视频乐缩、步态识别、运动跟踪、自动 会主席.主要研究方向为人工心理与情 挖制等作为负责人与主要参与人员完成国家自然科学基 感计算、服务机器人与数字人技术、网络化的信息服务系 金、国家"863"计划以及军工"863"计划多项,发表学术 统等.近年来主持完成国家“863”计划、国家自然科学基 论文50余篇,其中被sC1、EI检索30余篇. 金、国家科技攻关和国家"973”"计划子项目等多项科研项 目.发表学术论文180余篇,其中被SCI、EI检索60余篇,出 版专著5部. 2010年全国智能科学技术课程教学研讨会 征文通知 2010年全国智能科学技术课程教学研讨会将于2010年10月23-24日在中南大学召开 本次会议将围绕与智能科学技术相关的课程和专业的建设、改革等方面进行交流研讨,总结经验,取长补短, 促进智能科学技术的发展,引导和推动各高校智能科学技术课程的建设和教学水平的提高,诚挚欢迎从事智能科 学技术教学的教师和研究生积极参与,踊跃投稿, 1、征文范围包括(但不限于)): ①)与智能科学技术相关的课程(如智能科学基础、人工智能、智能控制、机器人学、专家系统、智能决策系统、智 能计算等课程)的教学、教改与创新:(②)与智能科学技术相关的专业(如智能科学与技术、计算机、自动化等),的教学 改革与建设以及各专业间关系:(3)教材建设经验与体会:(④))双语教学做法与经验:(⑤)课程和专业教学计划制定: (⑥)实验教学及其改革:7)教师队伍建设措施与经验;(⑧))相关课程和专业的未来发展思路和改革建议 2征文要求: 尚未录用和公开发表的论文,A4纸型双栏排版,Word2003格式,长度2-3页,最长不超过4页.论文应包括 中英文题目、中英文摘要、关键词、正文和参考文献等 3、投稿方式: 通过电子邮件发送PDF电子版一份(电子邮箱::ists2010@gmail..com),论文收到后,组委会即以邮件回复予 以确认 联系电话::15874291196(王勇)),15116286280(向健) 4、论文评审及出版 会议程序委员会将组织专家对征集的论文进行评审,根据评审结果向作者发出录用和修改通知.录用论文将 在《计算机教育》杂志上正式发表 5、重要日程: 论文投稿截止日期:1:2010年7月31日 录用通知发出日期:2010年8月20日 会议召开日期::2010年10月23-24日 6、会议地点 长沙-张家界(中国湖南) 7、会议组织 组织委员会主席::施荣华教授 程序委员会主席:蔡自兴教授 会议主席、组织委员会和程序委员会其他成员待开会前商定 8、主办单位 中国人工智能学会教育工作委员、中国计算机学会人工智能与模式识别专业委员会、中国人工智能学会智能: 机器人专业委员会、中国自动化学会智能自动化专业委员会、中国人工智能学会人工智能基础专业委员会、中南 大学信息科学与工程学院
刘冀伟,男,1962年生,副教授、博 士,北京科技大学信息工程学院自动化 系副主任,IEEE会员,中国人工智能 学会人工心理与情感计算专业委员 会理事.主要研究方向为图像处理、 视频压缩、步态识别、运动跟踪、自动 论文投稿截止日期: 2010年7月31日 录用通知发出日期: 2010年8月20日 会议召开日期: 2010年10月23-24日 控制等.作为负责人与主要参与人员完成国家自然科学基 金、国家"863"计划以及军工"863"计划多项,发表学术 论文50余篇,其中被SCI、EI检索30余篇. 联系电话: 15874291196(王勇) ,15116286280(向健) 6、会议地点 2010年全国智能科学技术课程教学研讨会将于2010年10月23-24日在中南大学召开. 本次会议将围绕与智能科学技术相关的课程和专业的建设、改革等方面进行交流研讨,总结经验,取长补短, 促进智能科学技术的发展,引导和推动各高校智能科学技术课程的建设和教学水平的提高.诚挚欢迎从事智能科 王志良,男,1956年生,国家二级教 授、博士生导师、博士,北京科技大学 电子信息系主任,中国人工智能学会人 工心理与人工情感专业委员会主任,第 一届国际情感计算和智能交互学术大 会主席.主要研究方向为人工心理与情 感计算、服务机器人与数字人技术、网络化的信息服务系 统等.近年来主持完成国家"863"计划、国家自然科学基 金、国家科技攻关和国家"973"计划子项目等多项科研项 目.发表学术论文180余篇,其中被SCI、EI检索60余篇,出 版专著5部. 学技术教学的教师和研究生积极参与,踊跃投稿 1、征文范围包括(但不限于) : (1) 与智能科学技术相关的课程(如智能科学基础、人工智能、智能控制、机器人学、专家系统、智能决策系统、智 能计算等课程) 的教学、教改与创新;(2) 与智能科学技术相关的专业(如智能科学与技术、计算机、自动化等) 的教学 改革与建设以及各专业间关系;(3) 教材建设经验与体会;(4) 双语教学做法与经验;(5) 课程和专业教学计划制定; (6) 实验教学及其改革;7) 教师队伍建设措施与经验;(8) 相关课程和专业的未来发展思路和改革建议. 3、投稿方式: 长沙-张家界(中国湖南) 7、会议组织 组织委员会主席: 施荣华教授 程序委员会主席: 蔡自兴教授 会议主席、组织委员会和程序委员会其他成员待开会前商定. 第3期 尚未录用和公开发表的论文,A4纸型双栏排版,Word 2003格式,长度2-3页,最长不超过4页.论文应包括 中英文题目、中英文摘要、关键词、正文和参考文献等. 中国人工智能学会教育工作委员、中国计算机学会人工智能与模式识别专业委员会、中国人工智能学会智能 机器人专业委员会、中国自动化学会智能自动化专业委员会、中国人工智能学会人工智能基础专业委员会、中南 大学信息科学与工程学院 2、征文要求: 239 4、论文评审及出版 8、主办单位 通过电子邮件发送PDF电子版一份(电子邮箱: ists2010@ gmail.com) .论文收到后,组委会即以邮件回复予 以确认. 会议程序委员会将组织专家对征集的论文进行评审,根据评审结果向作者发出录用和修改通知.录用论文将 在《计算机教育》杂志上正式发表. 崔朝辉,等: 分形图像编码算法的参数选择对算法性能的影响 2010年全国智能科学技术课程教学研讨会 征文通知 5、重要日程: