
第5卷第6期 智能系统学报 Vol.5 No.6 2010年12月 CAAI Transactions on Intelligent Systems Dec.2010 doi:10.3969/i.issn1673-4785.2010.06.009 灰度熵和混沌粒子群的图像多阈值选取 吴一全12,纪守新 (南京航空航天大学信息科学与技术学院,江苏南京210016;2南京大学计算机软件新技术国家重点实验室,江苏南京 210093)】 摘要:最大Shannon嫡阈值选取方法仅仅依赖于图像灰度直方图的概率信息,而没有直接考虑类内灰度级的均匀 性.为此提出了最大灰度嫡的阈值选取方法.首先给出了灰度嫡的定义及其单阈值选取方法,该灰度嫡与现有的仅 基于直方图分布的最大Shannon嫡不同,直接反映了类内灰度级的均匀性:其次导出了量化图像直方图的灰度熵单 阈值选取公式:最后将灰度熵单阈值选取推广到多阈值选取,提出了相应的快速递推算法,并进一步采用混沌小生 境粒子群优化算法寻找最佳多阈值.实验结果表明,与最大Shannon熵单阙值选取和基于粒子群的最大Shannon熵 多阈值选取方法相比,所提出方法的分割图像边缘、纹理更为准确,视觉效果明显改善 关键词:图像分割:阈值选取:灰度嫡:量化图像直方图:多阙值:混沌小生境粒子群优化 中图分类号:TP391.41;TN911.73文献标志码:A文章编号:16734785(2010)06052208 Multi-threshold selection for an image based on gray entropy and chaotic particle swarm optimization WU Yi-quan'2,JI Shou-xin' (1.School of Information Science and Technology,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China; 2.State Key Laboratory for Novel Software Technology,Nanjing University,Nanjing 210093,China) Abstract:The method of threshold selection based on maximal Shannon entropy depends only on the probability in- formation from a gray image histogram and does not immediately consider the uniformity of the gray scale within the cluster.Considering these facts,a method of threshold selection based on maximal gray entropy was proposed. First,gray entropy was defined and the method of single threshold selection was given.Being different from maxi- mal Shannon entropy based only on histogram distribution,the gray entropy reflects the uniformity of the gray scale immediately within the cluster.Then,the formulae of gray entropy based single threshold selection of a quantized image histogram were derived.Finally,the method of single threshold selection based on gray entropy was extended to multi-threshold selection.A corresponding fast recurring algorithm was proposed.Furthermore,a particle swarm optimization algorithm with a chaotic niche was adopted to find the best multi-threshold.Many experimental results show that,compared with the methods of single threshold selection based on maximal Shannon entropy and multi- threshold selection based on maximal Shannon entropy with particle swarm optimization,segmented images of the suggested method are more accurate in edge and texture,and their visual effect is improved significantly. Keywords:image segmentation;threshold selection;gray entropy;quantified image histogram;multi-threshold; particle swarm optimization of chaotic niche 图像分割就是把图像中具有特定含义的不同区 以获得最佳分割效果.在较早提出并进行定性和定 域分割开来,每一个区域都满足某种特性的一致性。 量比较研究的、有代表性的阈值选取方法中,由Ka 目标检测、特征提取和目标识别等,都依赖于图像 pur等人[)提出的最大Shannon熵阈值选取方法,通 分割的质量12].阈值分割是简单有效、应用广泛且 过引人信息论中的Shannon熵准则寻找最佳阈值, 易于实现的图像分割方法,其关键是自动选取阈值 因能产生较好的分割效果且简单有效,成为人们最 为关注的阈值选取方法之一.单阈值分割是通过一 收稿日期:201004-12. 个阈值把图像分成目标和背景2类区域,但实际图 基金项目:国家自然科学基金资助项目(60872065);航空科学基金资 助项目(20105152026);南京大学计算机软件新技术国家 像中往往含有灰度明显不同的多类目标.当最大 重点实验室开放基金资助项目(KFKT2010B17). Shannon熵单阈值选取推广到多阈值选取时[4],导 通信作者:吴一全.E-mail:nuaaimage@yahoo.com.cm

第6期 吴一全,等:灰度熵和混沌粒子群的图像多阈值选取 ·523· 致运算量随着目标类数的增加呈指数增长,为此人 H 们从不同角度相继提出了最大Shannon熵多阈值选 +血P、4.-么 1-P. +ln(1-P). 取的模拟退火算法5]、条件迭代算法[6、遗传算 L-1 法78们及粒子群优化算法9],不同程度地提高了多 式中:H,=含n,lhp,A=p,hp当(e)取最大 值时得到最大Shannon熵最佳阂值: 阈值选取的运行速度.但是上述最大Shannon熵单 阈值和多阈值选取方法中定义的Shannon熵仅仅依 。'=argm8)。 赖于图像灰度直方图中的概率信息,而设没有直接考 2 灰度熵的定义及其单阈值选取 虑图像中目标和背景类内灰度的均匀性,因此得到 的阈值分割效果还不够理想.此外,上述多阈值选取 若令 的优化方法中,基于粒子群的优化算法因其简单、易 f(m,n) Pm.n= (1) 实现、需调整的参数少而具有一定的优势.然而基本 ∑fm,n) (m,n)e 粒子群优化算法在搜索过程中容易陷入局部极值束 显然,子.cPm=L,则日标类的灰度嫡定义为 缚,难以保证收敛到全局最优解,此外还存在进化后 期的收敛速度慢和精度低等缺点, H。=-∑Paaln Pna (m,n)eC。 针对上述问题,本文首先定义了灰度熵,该灰度 f(m,n)In f(m,n) 嫡与现有的仅基于直方图分布的最大Shannon嫡不 (m,c。∑f(m,n) ∑f(m,n) (m,n)eC 同,其反映了类内灰度级的差异,是同一类内像素共 (m,neC。 同作用的的结果.灰度熵越大(小),类内的像素灰 ∑hipoln Poi(2) 度级差异越小(大).当总灰度嫡达到最大时,各类 ∑hi =0 内灰度级趋于均匀,据此选取的阈值可望改善分割 效果.为了提高灰度熵阈值选取的运行速度,可通过 式中:Pa= i 一,h:表示图像中灰度级出现的频数, 把原始图像以某一合适的步长进行量化,使得灰度 级的数目减少,以期降低搜索代价;另一方面,对于 由式(1)可见,目标类的像素灰度级f(m,n)越 多阈值选取,可采取快速递推方式,优化方法可考虑 均匀(即目标类中各像素的灰度级相近),各像素的 利用混沌小生境粒子群优化算法,通过将粒子分块, P就越接近,再根据式(2)中H,=.多cPah 并在寻优过程中对停止进化的粒子产生混沌扰动, Pmn这一部分可得,此时灰度嫡H。的值也就越大 使其跳出局部极值区,与基本粒子群算法相比,可提 同理,背景类的灰度熵H。表示为 高搜索最优阈值的速度和精确度, H=- 人 f(m,n) f(m,n) l现有的最大Shannon熵阈值选取 (m,n)eCp ∑f(m,n) ∑fm,n) (m,n)ECh (m,n》eCb L-1 -1 设尺寸为M×N图像中像素点(m,n)的灰度级 f代m,n)取0,1,…,L-1,对应的灰度级概率分布为 ∑.hi h.i L-1 PoP,…,PL-1,P:=1.现用阈值t按灰度级将图 i 式中:P=一.灰度熵瓜的值越大,背景类的灰 像像素划分成目标类C。={(m,n)lf(m,n)=0, 1,…,t}和背景类C.={(m,n)lf(m,n)=t+1,t+ 度级越均匀(即背景类中各像素的灰度级相近), 2,…,L-1},则目标和背景2类的概率分布分别为 目标类和背景类的总灰度熵为 会会…异和p…力,显然, (t)=H。+H=-∑h 最-1,某p=1神R-0<i-1, hi 则1-P=会 0.(t) i∑hi ,(0+[u.()]- 最大Shannon熵阈值选取方法的准则函数为 = 0-0(t) +ln[u-w.(t)]. (3) u-u (t)

·524: 智能系统学报 第5卷 式中: ln[u。-uo(te)]. (4) L-1 w.(t)=∑h,ini,o= hi, 式中: L-1 L-I w(,)=p.(xxnd,o.=p.(x)lnxd, u(t)= AA,u=三A =0 0(t)、u(t)的递推算法为 (.)=J,p.(x)d,4.=月p.()d w。(0)=0,n(0)=0, 相应量化图像的目标和背景类的总灰度熵 中,(t)为 r0(t)= hiln i=w(t -1)+h,tln t, 0 b,(5)=-0() ugo(g) In[ugo(t)] Lu,(t)=hi=u(t-1)+ht. t=1,2,…,L-1. ,=we2+ln[4,-p(,)]. (5) 4g-uo(tg) 灰度熵越大,类内的像素灰度级差异越小.当总 式中:wo(t)、0gu(t)、ug的表达式分别如下: 灰度熵Φ(t)达到最大时,目标类和背景类各自的像 素灰度级趋于均匀(即灰度级相近),此时对应的t ,)=a,(h= 便是最大灰度熵的最佳阈值T“: a1n.(alyh4 T=argm(). 由此可见该灰度熵与现有的仅基于直方图分布 。a(rh-la(n(ad]- 的最大Shannon熵不同,且直接反映了类内灰度级 的均匀性, s.()-1(40(p1,(6) r-0 3 量化图像直方图灰度熵单阈值选取 P(y)yIn ydy 对于灰度级直方图分布密集的图像,为了进一 △l·p.(△l·y)yIn ydy= 步降低运算量,采用量化图像的直方图进行灰度熵 1 阈值选取.这里所谓的量化图像是指把原始数字图 a7[w.-ln(A)·uJ, (7) 像的灰度级以某一合适的步长△1再次进行量化,使 得灰度级的数目减少,从而使阈值选取的搜索空间 4n4)=gn.() 缩小,有效地减少运算量.原图像的灰度级数目为 p.( 乙,则可以取量化步长41=是,使得灰度级数目变为 (8) 2.由于量化后直方图的形状基本不变],所以可 lde △l (L-1)/ 用较少的灰度级数目来计算图像的阈值.这样,可以 Pa(y)ydy 缩短运行时间,且所需存储单元数也大幅减少, (L-)/a 下面以连续形式的直方图来证明量化图像直方 ln.(A1=是 (9) 图与原始图像直方图的阈值关系.设原始图像和量 将式(6)~(9)代人式(5),经化简整理,得 化图像的直方图分别为P.(x)和P,(y),x∈D,y∈ 为,D表示灰度取值范围[0,L-1],则P(y)=A1· ()=-:号+1nu(w】 uom(△l·tn) P.(△1·y),y=点说明量化图像的直方图是原始图 o.-n(A:+n[4,-u(Wa)小.(10) ue-um(△l·tn) 像的直方图经尺度变换后的形式 比较式(10)和式(4)可知,量化图像的最佳阈 若用t和t。分别表示原始图像和量化图像所 值,和原始图像的最佳阈值存在如下关系: 用的分割阈值,则以连续形式来表达式(3)中原始 t。=△l·tg. 图像的目标类和背景类的总灰度嫡中.()为 由此可见,基于灰度熵嫡的图像阈值选取可以转 .(4)s-( +.1受8 化成其相应的量化图像的阈值选取.然而,由于图像 un(te 是数字化的,相应的直方图也非理想的连续曲线,由

第6期 吴一全,等:灰度嫡和混沌粒子群的图像多阈值选取 ·525· 此得到的阈值t。必然存在误差,因此量化步长△1= o(0,0)=0,u(0,0)=0, 票不宜太大为避免丢失太多的直方图信息,K比较 rw(0,t)= A,ai=(0,t-1)+hh, 合理的取值为5或6.本文按K=5处理, u(0,)=∑h,i=u(0,t-1)+h6 4基于混沌粒子群的灰度熵多阈值选取 t=1,2,…,L-1 4.1灰度熵多阈值选取公式及其递推算法 「0(tk-1+1,e)=o(0,k)-o(0,k-1), 由单阚值选取的灰度熵表达式(3)可以推广到 lu(tk-1+1,t)=u(0,tk)-u(0,t-i). 含有n个目标的多阈值选取情况,即 k=2,3,…,n 则当(,2,…,tn)最大时取得n个最佳阈值: Φ(t1,2,…,tn)=- h;i ∑hi (T,T2,…,T)=arg max{Φ(41,2,…,tn). 0s1h (X1,X2,…,Xa)和速度V=(V1,Vn,…,Vn.),X i=a-1+ 代表问题的解,粒子的优劣程度用所对应的适应度 函数来表示,V,表示粒子从当前位置移动到下一个 i=+1 ∑hi 位置的速度大小,首先对粒子群进行初始化,然后通 过迭代方式寻找最佳阈值.假设在第m·次迭代时 o(0,41) u(0,) +nu(0,t)- 刻,粒子l的最优解为pbest(m·),称为个体极值, o(4+1,+lnu(6+1,)-… 整个粒子群的最优解为gbest(m·),称为全局极值. u(61+1,2) 在m·+1时刻,按下式更新自己的速度: u(G,+i,+ha(41+1,)- 0(ta-1+1,tn) V(m*+1)=w'Vi(m*)+cr[pbest:(m*)- X:(m)]c2r2[gbest(m')-X(m")] w(tw+1,L-1) a(G,+1,L-i+l血(,+1,L-1).(11) 然后以速度V(m·+1)移动到下一个位置,即 X(m*+1)=X(m)+V(m*+1). 式中:1,t2,…,n为分割阈值,且0≤1<2<…< 式中:m表示当前迭代次数;学习因子c1=c2=2; tn-I <tn <L-1, 1、2是均匀分布在(0,1)上的随机数;惯性因子 w(0,t)=∑hiiln i, w·=wa-(wa-wia)m*/m,其中m=100 0 表示总迭代次数,0和0分别表示最大和最小惯 u(0,i)=∑h, 0 性因子,本文0=0.95,0=0.4.迭代更新过程 中,粒子速率限制在[Via,Vns],Vin=一Vnms w(4-1+1,e)=∑hni, -10.位置限制在允许范围内,最后输出的gbest为 i=%-1+1 k 全局最优解。 u(1+1,4)=∑hi,k=2,3,,n, 上述所描述的粒子群算法虽然简单,但它容易 i=g-1+1 L-1 陷入局部极值,搜索精度还不够高.而结合小生境策 o(6n+1,L-1)=∑hni, i=in+l 略全与混沌变异的混沌小生境粒子群优化算法,可 -1 避免算法早熟,保证搜索精度.本文使用的混沌映射 u(tn+1,L-1)=∑hi i=intl Logistic迭代方程为 为了缩短寻找n个最佳阈值的时间,下面给出 B1=8(1-Ba),k=1,2,…, 计算o(tk-1+1,tw)和u(tk-1+1,tk)的递推公式: B.∈(0,1),B。≠0.25,0.5,0.75

·526 智能系统学报 第5卷 迭代过程中,按下列方程对每个小生境种群中 6)如果满足最大迭代次数m,则停止迭代,输出 的最优个体pbest=[X,X2…X.…Xn]进行混沌迭 最佳阈值,并对图像进行多阈值分割,否则转2)· 代变异: 5 jP。=X4,in+Ba(X,mr-X4,m), 实验结果及分析 (12) lx1=(1-An)X+入nPe 利用上述提出的灰度嫡单阈值选取方法、量化 式中:入m,称为收缩因子,它决定了变量X的变异空 图像直方图的灰度熵单阈值选取方法、基于递推混 间,由式(13)得到. 沌小生境粒子群的灰度熵多阈值选取方法,对大量 入m=1-[(m·-1)/m] (13) 实际图像进行了阈值分割实验,并相应地与最大 式中:u用于控制收缩速度,本文中u=2. Shannon熵单阈值选取、文献[9]中基于粒子群的最 现利用基于混沌变异的小生境粒子群优化算法 大Shannon熵多阈值选取方法进行了比较,发现分 搜索最佳多阈值,算法具体步骤如下: 割后图像的主观视觉效果明显优于现有的这2种方 1)初始化小生境粒子种群.随机产生b(本文取 法.因篇幅所限,现以其中的House(256×256)、 为20)个粒子,并分成c(本文取为4)个子种群,粒 peppers(512×512)图像为例加以说明.图1~图2 子速度在[Vn,Vms]上随机产生; 分别给出了2幅原始灰度级图像(a)及灰度熵单阈 2)根据式(11)计算每个粒子的适应度,找出每 值选取(©)、基于递推混沌小生境粒子群的灰度熵 个小生境种群中的最优粒子和全局最优粒子; 多阈值选取(d)、(e)、量化图像直方图的灰度嫡单 3)计算2个粒子种群最优个体pbest(m·)与 阈值选取(f)、最大Shannon熵单阈值选取(g)、基于 pbest,(m')之间的距离dg,若d,<R.iae(小生 粒子群的最大Shannon嫡多阈值选取(h)和(i)等方 境半径,本文取为20),比较2个小生境最优个体的 法分割后的图像,相应的最佳阈值列于表1中,本文 适应度,低者置零,高者保持不变.对置零的最优个 中所有算法均是在Intel Celeration(R)CPU2. 体重新初始化,并在其所在的小生境内重新选择最 66GHz/512MB内存/Matlab7.0环境中运行的,图像 优个体,直至任意2个小生境最优个体之间的距离 分割的运行时间也一并列于表1.基于递推混沌小 deaz≥Rniche 生境粒子群的灰度嫡多阈值选取方法以及基于粒子 4)按式(12)对所有小生境最优个体的位置进 群的最大Shannon熵多阈值选取方法的粒子个数均 行变尺度混沌变异,进一步提高搜索精度: 为20,最大迭代次数分别为50和100. 5)更新每个粒子的位置和速度; ×10 50100150200250 (a)原始图像 (b)直方图 (c)灰度嫡单侧值 d)灰度嫡双圆值 (e)灰度嫡阈值 (量化图像前方图单谢值

第6期 吴一全,等:灰度嫡和混沌粒子群的图像多阈值选取 ·527 (g)最大Shannon嫡单阀值 (h)最大Shannon?螭双值 (i)最大Shannon物三值 图1 House图像及其分割结果 Fig.1 House image and segmentation results 45*10 4 36 0通 50100150200250 a)原始图像 (b)直方图 (c)灰度熵单值 d灰度璃双阈值 (e)灰度熵 ()量化图像直方图单碳值 (g)最大Shannon嫡单阙值 (h)最大Shannon?熵双恸值 (i)最大Shannon?嫡阚值 图2 Peppers图像及其分割结果 Fig.2 Peppers image and segmentation results 表1图像分割的阈值及运行时间的比较 Table 1 The comparison of threshold and processing time of image segmentation 单阙值 双阈值 三阈值 图像 量化图像 最大 基于粒子 基于混沌 基于粒子 基于混沌 灰度嫡 直方图 群的最大 粒子群的 群的最大 粒子群的 Shannon熵 灰度嫡 Shannon墒 灰度嫡 Shannon熵 灰度熵 103 127 120 (101,194) (63,113,194) (98,121,180) House 阚值 (113,179) 时间/g 0.015 0.015 0.012 0.344 0.315 0.407 0.401 阚值 168 91 96 (107,174) (80,121) (98,138,182) (73,93,139)》 Peppers 时间/s0.032 0.032 0.026 0.438 0.438 0.484 0.453
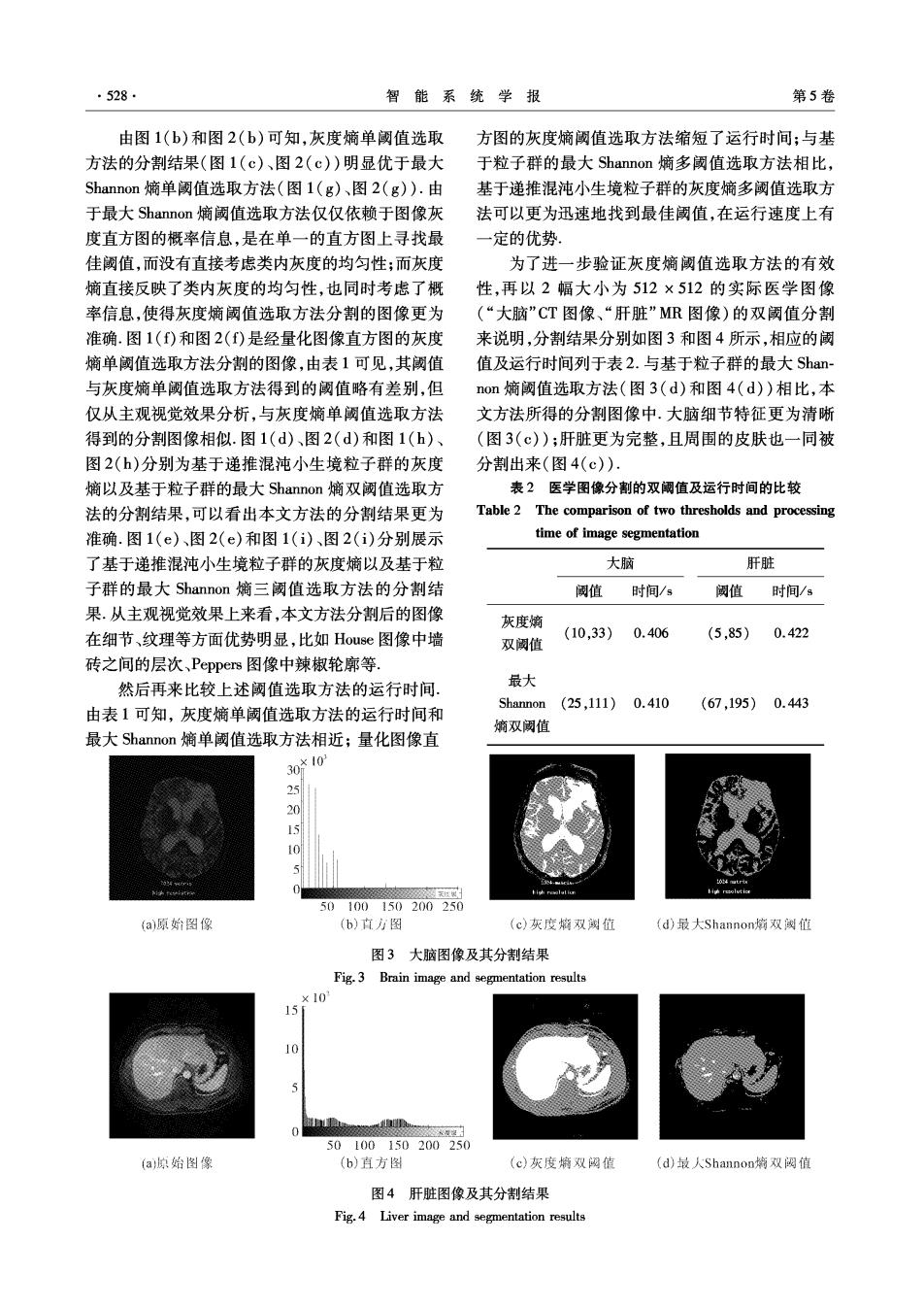
·528. 智能系统学报 第5卷 由图1(b)和图2(b)可知,灰度熵单阈值选取 方图的灰度熵阈值选取方法缩短了运行时间;与基 方法的分割结果(图1(c)、图2(c))明显优于最大 于粒子群的最大Shannon嫡多阈值选取方法相比, Shannon熵单阈值选取方法(图1(g)、图2(g)).由 基于递推混沌小生境粒子群的灰度熵多阈值选取方 于最大Shannon熵阈值选取方法仅仅依赖于图像灰 法可以更为迅速地找到最佳阈值,在运行速度上有 度直方图的概率信息,是在单一的直方图上寻找最 一定的优势. 佳阈值,而没有直接考虑类内灰度的均匀性;而灰度 为了进一步验证灰度熵阈值选取方法的有效 熵直接反映了类内灰度的均匀性,也同时考虑了概 性,再以2幅大小为512×512的实际医学图像 率信息,使得灰度熵阈值选取方法分割的图像更为 (“大脑”CT图像、“肝脏”MR图像)的双阈值分割 准确.图1()和图2(f)是经量化图像直方图的灰度 来说明,分割结果分别如图3和图4所示,相应的阈 熵单阈值选取方法分割的图像,由表1可见,其阈值 值及运行时间列于表2.与基于粒子群的最大Shan- 与灰度嫡单阈值选取方法得到的阈值略有差别,但 non熵阈值选取方法(图3(d)和图4(d))相比,本 仅从主观视觉效果分析,与灰度嫡单阈值选取方法 文方法所得的分割图像中.大脑细节特征更为清晰 得到的分割图像相似.图1(d)、图2(d)和图1(h)、 (图3(©)):肝脏更为完整,且周围的皮肤也一同被 图2()分别为基于递推混沌小生境粒子群的灰度 分割出来(图4(c)) 熵以及基于粒子群的最大Shannon嫡双阈值选取方 表2医学图像分割的双阑值及运行时间的比较 法的分割结果,可以看出本文方法的分割结果更为 Table 2 The comparison of two thresholds and processing 准确.图1(e)、图2(e)和图1(i)、图2(i)分别展示 time of image segmentation 了基于递推混沌小生境粒子群的灰度熵以及基于粒 大脑 肝脏 子群的最大Shannon嫡三阈值选取方法的分割结 阈值 时间/s 阙值 时间/s 果.从主观视觉效果上来看,本文方法分割后的图像 灰度嫡 在细节、纹理等方面优势明显,比如Hous图像中墙 (10,33) 0.406 (5,85)0.422 双阙值 砖之间的层次、Peppers图像中辣椒轮廓等. 然后再来比较上述阈值选取方法的运行时间 最大 Shannon(25,111)0.410 (67,195)0.443 由表1可知,灰度熵单阈值选取方法的运行时间和 熵双阙值 最大Shannon熵单阈值选取方法相近;量化图像直 3010 25 20 15 50100150200250 {a)原始图像 (b)直方图 (c)灰度幢双值 (d)最大Shannon痴双谢值 图3大脑图像及其分割结果 Fig.3 Brain image and segmentation results ×10 15 10 o 50100150200250 (a)惊始图像 (b)直方图 (c)灰度熵双网值 (d)最人Shannon熵双阙值 图4肝脏图像及其分割结果 Fig.4 Liver image and segmentation results

第6期 吴一全,等:灰度痛和混沌粒子群的图像多阙值选取 ·529· 6结束语 LUO Xiping,TIAN Jie.The ICM algorithm for multi-level threshold selection by maximal entropy criterion[J].Journal 本文给出的灰度熵的定义与现有的仅基于直方 of Software,2000,11(3):379-385. [7]王毅,牛奕龙,田沄,等.基于改进遗传算法的最佳嫡多 图分布的最大Shannon嫡不同,且直接反映了类内 阈值三维医学图像分割算法[J].西北工业大学学报, 灰度的均匀性,据此得到的阈值选取方法改善了图 2007.25(3):442445. 像分割效果;量化图像直方图的灰度熵阈值选取方 WANG Yi,NIU Yilong,TIAN Yun,et al.A more stable 法降低了搜索代价;提出的采用快速递推方式及混 and accurate genetic algorithm for segmentation of 3-D medi- 沌小生境粒子群优化寻找灰度熵最佳多阈值的方 cal images[J].Joumal of Northwestern Polytechnical Uni- versity,2007,25(3):442-445. 法,缩短了阈值选取的运行时间.针对实际灰度图像 [8]WANG Y,FAN YY,NIU Y L,et al.Effective immune 进行的大量实验结果表明,与最大Shannon熵单阈 genetic algorithm for segmentation of 3D brain images[J]. 值选取和基于粒子群的最大Shannon熵多阈值选取 Joural of System Simulation,2008,20(15):4136-4140. 方法相比,本文方法的分割性能更为优越.下一步的 [9]韦苗苗,江铭炎.基于粒子群优化算法的多阚值图像分 研究工作是基于二维灰度熵的图像阈值选取,这也 割[J].山东大学学报:工学版,2005,35(6):118-121. WEI Miaomiao,JIANG Mingyan.Multilevel thresholding 是下一篇研究论文的主题, methods for image segmentation based on particle swarm op- 参考文献: timization[J].Joural of Shandong University:Engineering Science,2005,35(6):118-121. [1]陈小波,程显毅.一种基于MAS的自适应图像分割方法 [10]严学强,叶秀清,刘济林,等.基于量化图像直方图的 [J].智能系统学报,2007,2(4):80-85. 最大Shannon嫡阙值处理算法[J刀.模式识别与人工智 CHEN Xiaobo,CHENG Xianyi.An adaptive image segmen- 能,1998,11(3):352-358. tation technique based on multi-Agent system J].CAAI YAN Xuegiang,YE Xiuqing,LIU Jilin,et al.Maximal Transactions on Intelligent Systems,2007,2(4):80-85. entropy image thresholding algrithm based on the histogram [2]王科俊,郭庆昌.基于粒子群优化算法和改进的Snake defined on quantization image[J].Pattem Recognition and 模型的图像分割算法[J].智能系统学报,2007,2(1): Artificial Intelligence,1998,11(3):352-358. 53-58. [11]贾东立,张家树.基于混沌变异的小生境粒子群优化算 WANG Kejun,GUO Qingchang.Image segmentation algo- 法[J].控制与决策,2007,22(1):117-120. rithm based on the PSO and improved Snake model [J]. JIA Dongli,ZHANG Jiashu.Niche particle swarm optimi- CAAI Transactions on Intelligent Systems,2007,2 (1 ) zation combined with chaotic mutation[J].Control and 53-58. Decision,2007,22(1):117-120. [3]KAPUR J N,SAHOO P K,WONG A K C.A new method 作者简介: for grey-level picture thresholding using the entropy of the 吴一全,男,1963年生,教授,博 histogram[].Computer Vision,Graphics and Image Pro- 土,主要研究方向为图像处理与模式 cessing,1985,29(1):273-285. 识别、目标检测与跟踪、智能信息处理 [4]曹力,史忠科.基于最大Shannon熵原理的多阈值自动 等.在国内外核心刊物和国际学术会 选取新方法[J].中国图象图形学报,2002,7(5):461 议上发表学术论文90余篇. 465. CAO Li,SHI Zhongke.An automatic multilevel threshol- ding method based on maximal entropy[J].Journal of Im- 纪守新,男,1984年生,硕士研究 age and Graphics,2002,7(5):461-465. 生,主要研究方向为图像处理与目标检 5]CHANG H C,CHEN J R,LI J G.Threshold selection 测等. based on fuzzy c-partition entropy approach [J].Pattemn Recognition,1998,31(7):857-870. [6]罗希平,田捷.用最大Shannon嫡原则作多阈值选择的 条件迭代算法[J].软件学报,2000,11(3):379-385