
第5卷第4期 智能系统学报 Vol.5 No.4 2010年8月 CAAI Transactions on Intelligent Systems Aug.2010 doi:10.3969/i.issn.16734785.2010.04.010 求解旅行商问题的近似多项式算法 高尚,房靖 (江苏科技大学计算机科学与工程学院,江苏镇江212003)】 摘要:旅行商问题是一个典型的组合优化问题,易于描述却难于求解.对于大规模SP问题,目前仍未有非常有效 的方法.针对弹性网络算法在求解旅行商问题中时间性能方面的不足,提出了一种快速的求解算法.在弹性网络算 法基础上,提出了求解旅行商问题的扩张方法和收缩方法,它们时间复杂性低于O(W),经过比较扩张方法的效果 比较理想.在扩张方法的基础上,提出随机扩张方法和完全扩张方法,完全扩张方法的时间复杂性低于O(N),仍然 是一个多项式算法.实例表明,完全扩张方法是一个快速且有效的算法. 关键词:扩张方法;收缩方法;旅行商问题 中图分类号:TP301.6文献标识码:A文章编号:16734785(2010)040342-05 A polynomial approximation algorithm for the traveling salesmen problem GAO Shang,FANG Jing (School of Computer and Engineering,Jiangsu University of Science and Technology,Zhenjiang 212003,China) Abstract:The Traveling Salesman Problem (TSP)is a typical combinational optimization problem which is easy to describe and hard to solve.For large-scale TSP problems,an effective solution has yet to be found.To improve the time performance of the elastic net method in solving large scale TSPs,faster algorithms were investigated.Use of the elastic net method,the expansion method and the shrink method were proposed.The time complexities of these algorithms were less than 0(N).After comparison and analysis it was clear that the results of the expansion method were comparatively ideal.Based on analysis of the expansion method,a stochastic expansion method and a complete expansion method were developed.The time complexity of the complete expansion method was less than 0(N),and it was still a polynomial algorithm.Practical examples showed that the complete expansion method is fast and efficient. Keywords:expansion method;shrink method;traveling salesman problem 旅行商问题(traveling salesman problem)可以描多项式方法 述为有一个推销员从某城市出发走遍所有的城市, 且每个城市只能走一次,最后返回原处,如何选择路 1扩张方法 线使所走路程最短.TSP问题是一个NP完全问题, 1987年,R.Durbin和D.Willshaw提出了一种 对于一个V个城市的TSP问题,可能的路径数是一 被称为弹性网络的新模型1o11来求解TSP问题.这 个组合数(N-1)/2,随着城市数目N的增大,问 一模型考虑的是欧氏空间中的TSP问题,它把一条 题的规模呈指数式增大.目前求解TSP问题的主要 TSP可行路径看作是从一条由M个节点构成的闭 方法有模拟退火算法14、遗传算法1s6、,启发式 合路径到TSP城市的映射.这条闭合路径被称为 搜索法、Hopfield神经网络算法、蚁群算法[891等. “弹性带”(elastic band),一般来说取M=2.5N.当 本文在弹性网络算法的基础上提出2种简单的近似 对于每一个城市都有一个节点与它重合时,“弹性 带”的总长度就是TSP路径总长度的一个近似.弹 收稿日期:200907-13. 性网络算法的思想就是不断调整这些节点的位置, 基金项目:浙江大学CAD&CG国家重点实验室开放课题(A0704);江 苏省高校自然科学基础研究课题(08KB520003). 使得“弹性带”在覆盖所有城市的同时,总的长度尽 通信作者:高尚.E-mail:gao_hang@hotmial.com 可能小.弹性网络算法通过2种作用力来控制弹性
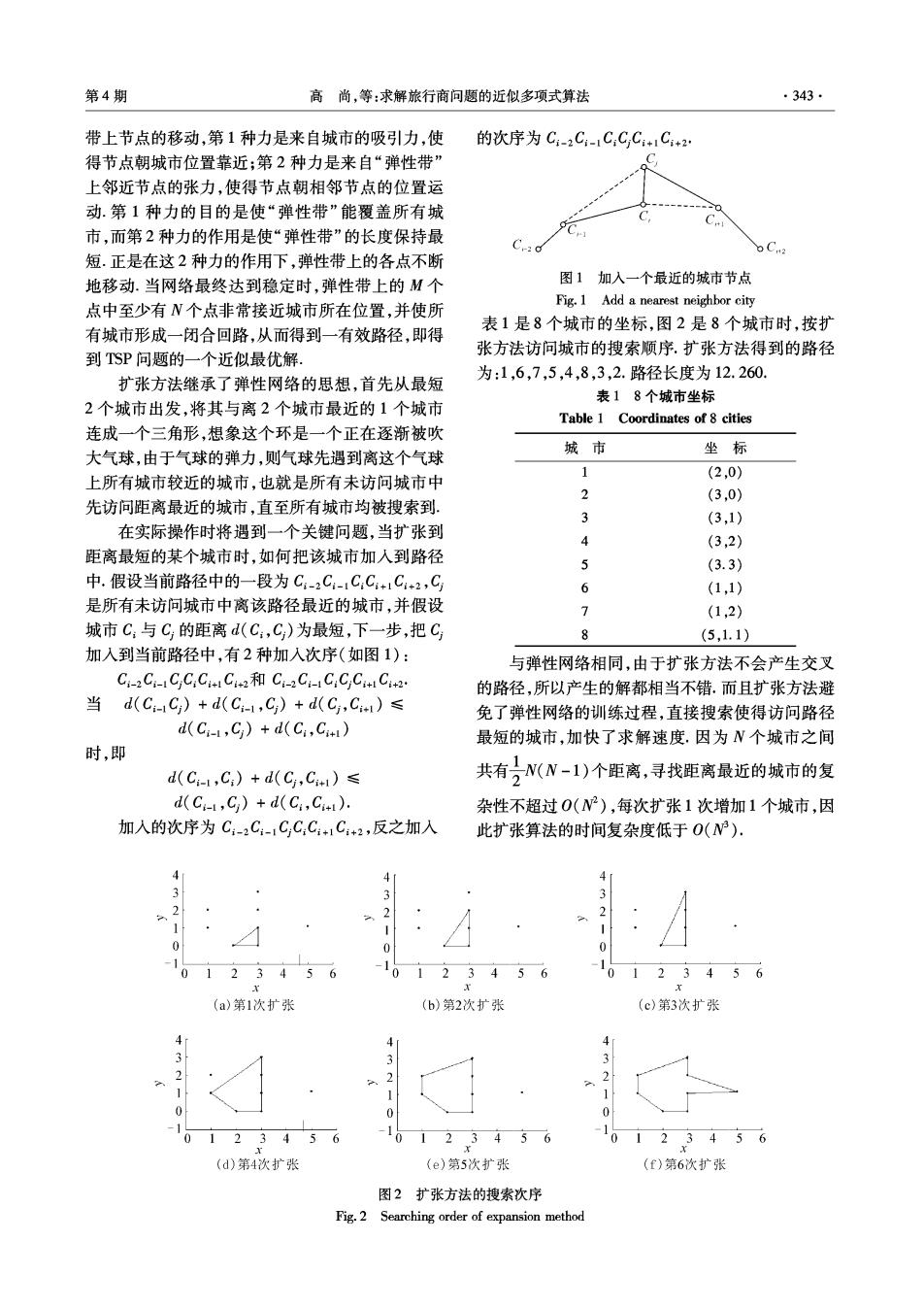
第4期 高尚,等:求解旅行商问题的近似多项式算法 ·343· 带上节点的移动,第1种力是来自城市的吸引力,使 的次序为C:-2C:-1C:CC+1C+2 得节点朝城市位置靠近;第2种力是来自“弹性带” 上邻近节点的张力,使得节点朝相邻节点的位置运 动.第1种力的目的是使“弹性带”能覆盖所有城 C 市,而第2种力的作用是使“弹性带”的长度保持最 短.正是在这2种力的作用下,弹性带上的各点不断 地移动.当网络最终达到稳定时,弹性带上的M个 图1加入一个最近的城市节点 Fig.1 Add a nearest neighbor city 点中至少有N个点非常接近城市所在位置,并使所 表1是8个城市的坐标,图2是8个城市时,按扩 有城市形成一闭合回路,从而得到一有效路径,即得 张方法访问城市的搜索顺序.扩张方法得到的路径 到TSP问题的一个近似最优解. 为:1,6,7,5,4,8,3,2.路径长度为12.260 扩张方法继承了弹性网络的思想,首先从最短 表18个城市坐标 2个城市出发,将其与离2个城市最近的1个城市 Table 1 Coordinates of 8 cities 连成一个三角形,想象这个环是一个正在逐渐被吹 大气球,由于气球的弹力,则气球先遇到离这个气球 城市 坐标 1 上所有城市较近的城市,也就是所有未访问城市中 (2,0) 2 (3,0) 先访问距离最近的城市,直至所有城市均被搜索到 3 (3,1) 在实际操作时将遇到一个关键问题,当扩张到 4 (3,2) 距离最短的某个城市时,如何把该城市加入到路径 5 (3.3) 中.假设当前路径中的一段为C:-2C:-1C,C+1C+2,C 6 (1,1) 是所有未访问城市中离该路径最近的城市,并假设 > (1,2) 城市C:与C的距离d(C:,C)为最短,下一步,把C 8 (5,1.1) 加入到当前路径中,有2种加入次序(如图1): 与弹性网络相同,由于扩张方法不会产生交叉 Ci-2C:-ICC:CiC2 C-2C-1CCCi C2. 的路径,所以产生的解都相当不错.而且扩张方法避 当d(C-C)+d(C-1,C)+d(C,C)≤ 免了弹性网络的训练过程,直接搜索使得访问路径 d(Ci-,C)+d(Ci,Ci) 最短的城市,加快了求解速度.因为N个城市之间 时,即 d(C-1,C)+d(C,C+i)≤ 共有)N(N-1)个距离,寻找距离最近的城市的复 d(Ci,C)+d(C:,Cim). 杂性不超过0(N2),每次扩张1次增加1个城市,因 加人的次序为C:-2C-1C,C,C+1C+2,反之加入 此扩张算法的时间复杂度低于O(N3). 4 3 3 2 2 2 0 0 0 -1 0123456 -101234 5 2 (a)第1次扩张 (b)第2次扩张 (c)第3次扩张 4 4 3 2 2 0 0 23456 0123456 0123456 (d)第4次扩张 (e)第5次扩张 (f)第6次扩张 图2扩张方法的搜索次序 Fig.2 Searching order of expansion method

.344 智能系统学报 第5卷 2收缩方法 (xm,yim)、(xmy)和(xmn,yme).这4个边角有 可能与原来城市坐标重叠,也可能不重叠(如图3 与扩张方法思路相反的方法是收缩,首先确定 中“0”).然后找出分别与上面4个边角点最近的4 4个边角点,方法如下:分别比较出所有城市的x轴 个边角城市(如图中的“+”),这4个边角城市作为 的最小值x和最大值xa,y轴的最小值yan和最 初始路径 大值ymr,这样就得到4个边角坐标(xia,ymin)、 4 4 3 3 3 0 0 0 -1 1 0123456 10123456 0123456 (a)4个边角 (b)初始路径 (c)第1次收缩 4 3 3 2 0 0 0 123456 0123456 0123456 (d)第2次收猫 (e)第3次收缩 (f)第4次收缩 图3收缩方法的搜索次序 Fig.3 Searching order of shrink method 接下来的工作与扩展方法类似,搜索所有未访 100 问城市中距离离最近的城市,直至所有城市均被搜 形 索到。与扩张算法类似,其时间复杂度也低于 60 0(W3). 同样的例子,图3是扩张方法访问城市的搜索 顺序.搜索方法得到的路径为:1,2,3,4,8,5,7,6.路 径长度为12.602. 20 40 60 80100 2种方法的结果不一样,解的质量还可以接受, 由于收缩方法选择初始的4个城市不能保证把所有 图4 Oliver30的TSP最好的解 城市都包含四边形中,搜索过程中有时收缩,有时扩 Fig.4 The optimal tour of Oliver30 100 张,因此该方法的效果不如扩张方法好。 3实例分析 60 着重分析扩张方法,分别选用Oliver30(最好解 为420.15)和at48(TSPLIB提供的最好解为33522) 作为实验例子来研究.图4显示了目前Oliver30最 好解,图5显示了扩张方法解Oliver30的TSP解,路 20 40 ,60 80100 径长度为536.56.图6显示了att48最好解,图7显 图5扩张方法的Olivers30的TSP解 示了扩张方法求att48的解,路径长度为42439 Fig.5 The tour of Oliver30 by expansion method

第4期 高尚,等:求解旅行商问题的近似多项式算法 ·345· 610 城市选23,路径长度为3862.94(图9).虽然完全 扩张方法不一定能找到最优解,但能在较短时间内 找到“次优解”也能满足实际需要. ×103 ×10 图6at48的最好的解 Fig.6 The optimal tour of att48 610 810 图9完全扩张方法的a48的解 Fig.9 The tour of att48 by complete expansion method 4结束语 在弹性网络算法基础上,提出了扩张方法和收 缩方法,它们时间复杂性低于O(N),经过比较扩 ×10 张方法的效果比较好.在扩张方法的基础上,提出随 图7扩张方法的a48的解 机扩张方法和完全扩张方法,完全扩张方法的时间 Fig.7 The tour of att48 by expansion method 复杂性低于O(N),仍然是一个多项式算法,运行 扩张方法首先从最短2个城市出发,将其与离 速度极快.由于TSP问题代表着一类组合优化问 2个城市最近的1个城市连成一个三角形,然后扩 题,并且TSP问题在实际工程中有许多应用,如电 展.实际上可以先随机挑选一个城市,然后找离该城 子地图、交通诱导、VLSI布线等.在很难找到最优解 市最短的第2个城市,后面的步骤与扩展方法相同, 的情况下,由完全扩张方法找到的“次优解”可满足 此方法称为随机扩张方法,这样随机的选取会增大 实际工程需要. 更好解的几率 参考文献: 由于扩张方法的复杂性为O(W3),复杂性不 高,可采取完全枚举法,分别以各个城市为第1个城 [1]邢文循,谢金星.现代优化计算方法[M].北京:清华大 市,然后找离该城市最短的第2个城市,后面的步骤 学出版社,1999:90-129. [2]高国华,沈林成,常文森.求解TSP问题的空间锐化模拟 与扩展方法相同,最后从N个结果中挑选最好的结 退火算法[J].自动化学报,1999,25(3):425428. 果,此方法称为完全扩张方法.很显然其时间性低于 GAO Guohua,SHEN Lincheng,CHANG Wensen.Using 0(W). simulated annealing algorithm with search space sharpening 100 to solve traveling salesman problem[J].Acta Automatica 0 Sinica,1999,25(3):425428. [3]KIRKPATRICK S,GELATT JR,VECCHI J R.Optimization by simulated annealing[J].Science,1983,220:671-680. [4]康立山,谢云,尤矢勇,等.模拟退火算法[M].北京:科 20 学出版社,1994:150-151 [5]谢胜利,唐敏,董金祥.求解TSP问题的一种改进的遗传 20 40 6080100 算法[J].计算机工程与应用,2002,38(8):5860. XIE Shengli,TANG Min,DONG Jinxiang.An improved 图8完全扩张方法的Oliver30的解 genetic algorithm for TSP problem[J].Computer Engineer Fig.8 The tour of Oliver30 by complete expansion method ing and Applications,2002,38(8):58-60. 对于Oliver30问题,完全扩张方法最好的结果 [6]喻镝,凌捷,谢晓峰.用遗传算法求解CTSP[J].广东工 是:第1个城市选29,路径长度为485.11(图8).对 业大学学报,2000,17(5):5255. 于a48问题,完全扩张方法最好的结果是:第1个 YU Di,LING Jie,XIE Xiaofeng.Solving CTSP with genet-

.346. 智能系统学报 第5卷 ic algorithm[J].Journal of Guangdong University of Tech- [10]DURBIN R,WILISHAW D.An analogue approach to the nol0gw,2000,17(3):52-55. traveling salesman problem using an elastic net method [7]张立明.人工神经网络的模型及其应用[M].复旦大学 [J].Nature,1987,326:689691. 出版社,1994:97-98. [11]白艳萍,胡红萍.一个改进的弹性网络算法求解TSP问 [8]张纪会,徐心和.具有变异特征的蚁群算法[J].计算机 题[J].华北工学院学报,2005,26(4):235238. 研究与发展,1999,36(10):1240-1245. BAI Yanping,HU Hongping.A modified elastic net algo- WU Qinghong,ZHANG Jihui,XU Xinhe.An ant colony al- rithm for traveling salesman problem[J].Journal of North gorithm with mutation features[J].Journal of Computer Re- China Institute of Technology,2005,26(4):235-238 search and Development,1999,36(10):1240-1245. 作者简介: [9]马良,项培军.蚂蚁算法在组合优化中的应用[J].管理 高尚,男,1972年生,教授,主要 科学学报,2001,4(2):32-37. 研究方向智能计算等. MA Liang,XIANG Peijun.Applications of the ant algorithm to combinatorial optimization[J].Journal of Management Sciences in China,2001,4(2):32-37. HZInternational workshop on quality of service management of wireless networks(IWQSWN 2010) This workshop is to be held in conjunction with the 2010 IEEE Asia-Pacific Services Computing Conference at Hang- zhou,China.The objective of this workshop is to review the state of the art research in the quality of service (QoS)man- agement and diagnosis of wireless networks,as well as to explore future research directions in this area.Quality of service of wireless networks refers to the collective service performances with respect to the user expectation and the network con figuration.Over the years,the wireless networks have not only expanded in their sizes,such as geographical area and number of nodes,but also in the variety of services,users,and deployment environments.Small mobile devices that allow instantaneous high speed information access and data processing have radically changed the way of our living.Moreover, the development of ad-hoc networks allows the easy formation of wireless networks for information sharing and data gather- ing. Indexed by SCI&EI December 6-10,2010,Hangzhou,China Topics of Interest Topics of interest include (but are not limited to): ·fault diagnosis diagnosis middleware reconfigurable networks performance evaluation ·QoS evaluation model self-healing networks Adaptable resource management Network simulation platforms QoS-oriented network planning See more information at http://apscc2010.hdu.edu.cn