
第5卷第6期 智能系统学报 Vol.5 No.6 2010年12月 CAAI Transactions on Intelligent Systems Dec.2010 doi:10.3969/i.i8sn.16734785.2010.06.010 交会对接最后逼近段姿轨耦合控制 李鹏2,陈兴林2,宋申民2,李敏利2 (1.湘潭大学信息工程学院,湖南湘潭411105:2.哈尔滨工业大学航天学院,黑龙江哈尔滨150001) 摘要:针对交会对接最后逼近段的制导律和姿态控制律的设计问题,首先对逼近段轨道与姿态的耦合问题进行了 分析,并利用高阶滑模控制设计了最后逼近段的姿轨控制系统;然后设计了基于H方程的直线型制导律;最后对 所采用的直线型变结构制导律和最后逼近段相对姿态控制律进行了仿真.仿真结果表明所设计的控制系统满足对 接要求。 关键词:交会对接;最后逼近段;姿轨耦合控制 中图分类号:TP18;TN911.23文献标志码:A文章编号:16734785(2010)06053004 Research on an attitude and orbit coupling control over the final approach phase of rendezvous and docking LI Peng'2,CHEN Xing-lin2,SONG Shen-min2,LI Min-li2 (1.College of Information Engineering,Xiangtan Univesity,Xiangtan 411105,China;2.School of Astronautics,Harbin Institute of Technology,Harbin 150001,China) Abstract:To achieve the high precision requirement in the final approach phase of autonomous space rendezvous and docking(RVD)on a relative attitude,first an analysis was made on the coupling of attitude and orbit.Next, the high-order sliding mode (HOSM)controller was used to design the attitude and orbit control system in the final approach phase.After that,a beeline guidance law based on the Hill equation was designed.The attitude control strategy shown here used the HOSM controller.Lastly,with the help of Simulink software,a simulation was carried out in terms of the linear variable structure guidance law and relative attitude control law.The results of simulation show that the designed control system meets the requirements of docking. Keywords:rendezvous and docking;final approach phase;coupling control of attitude and orbit 保证空间飞行器在复杂的空间环境中能够更加 定的方位和指向,或进行方位和指向的机动。 持久、稳定地在轨运行,已成为目前空间技术领域亟 待解决的重要问题.交会对接技术是在轨维护与服 1姿轨耦合控制概述 务的先决条件之一,只有通过交会对接,才能给航天 在最后逼近段,一般情况下追踪航天器沿视线 器补给燃料、更换设备、维护仪器、维修在轨故障卫 方向作直线型受迫运动逼近目标航天器对接口(对 星等.为了保证安全交会对接和对接精度,必须考虑 接港),因此最终逼近段也常称为“最终平移段”门, 轨道和姿态的耦合控制.轨道控制使飞行器在星体 在这个阶段,为了保证安全交会对接和对接精度,必 的引力场中牵人和保持预定的空间运动轨迹,或在 须考虑轨道和姿态的耦合控制.图1为姿轨耦合控 多个星体的引力场中运动轨迹的转移;姿态控制则 制的控制框图,上部分为姿态控制回路,下部分为位 使飞行器的构型布局在空间轨道控制运动中保持预 置控制回路.根据相对位置的初始和终点状态算出 期望的轨迹,也就是要求追踪航天器按所求的轨迹 收稿日期:201002-16. 逼近目标航天器,直到2个航天器对接上为止.据这 基金项目:国家“863”计划资助项目(2006AA0488,2007AA0987, 2008AA0987). 条所要求逼近目标航天器的轨迹算出相应的期望姿 通信作者:李鹏.E-mail:pengli.hit@gmail.com 态角度,然后根据实际信息进行相对位置和相对姿

第6期 李鹏,等:交会对接最后逼近段姿轨耦合控制 ·531· 态控制. 式中:T为目标航天器轨道坐标系O®YoYoZ。与追 g(,,w) 姿态控制 q=(,8,9) 踪航天器本体坐标系OcX:YgZB之间的转换矩阵. 零点 (速度观察器和 保持器 坐标转换 反映了姿态偏差对轨道的影响,这是轨道和姿态耦 控制规律) 合的一个方面,F为常值推力. (a,y,) 沿视线接近时,设相对位矢x的偏航角和视线 航天器 航大器 位置和姿态测量及 倾角分别为中、0,追踪航天器本体坐标系 初 动力学 制导设计 计算机数据处理 OCXEYEZE跟踪目标航天器轨道坐标系ORX,YoZo, 始 (p,a,B) 条 (pnB9) (p0中)=(00,中,) 件 零点pa,B 坐标转换 c(q) 保持器 T(p,0,)=T(0,0,中), 坐标转换 位置控制(速度观 察器和控制规律, 坐标转换 sin,=,co0s女,=起】 Pw P灯 PF(Xp Vn Z p(x,y,z) 虚线表示位誉初始条件提供给制导系统设计 sin0。=。,co88,=Pg p (p,日,wu】 p=V√R+y2+2, 图1姿轨耦合控制框图 pw=√e2+y Fig.1 Coupled attitude and orbit control 可见,在沿视线接近模式下方向角和俯仰角完 2最后逼近段姿轨耦合问题分析 全取决于2个航天器的相对位置偏差,进一步求导 得56例 2.1相关坐标系说明 地心惯性坐标系O,X,Y,Z,目标轨道坐标系 「或,=y-yE OgXoYoZo,追踪航天器体坐标系OcXgYgZE,视线坐 x2+y2 标系ORXsYsZs,原点在目标航天器的质心.设p为 6=+-(2+)2 追踪航天器相对于目标航天器的位矢,且与Ox,重 (x2+y2+z2)We2+y 合,p与Ox,y,平面的夹角为0,称为视线角p在 由上式可见,中,、0,不仅和2个航天器的相对 Oxy,上的投影与Ox,的夹角为山,称其为偏离 位置相关,而且还和其相对速度相关,所以在沿视线 角23) 接近模式下轨道和姿态运动是严重耦合的, 2.2轨道与姿态的耦合问题分析 3姿态-轨道耦合控制系统设计 最终平移段的相对运动一般采用目标航天器轨 道坐标系.假设目标航天器位于高度为500km的圆 一般情况下,目标航天器为非机动的合作目标, 轨道上,则追踪航天器相对于目标航天器的相对运 相对于惯性或者是目标航天器轨道坐标系保持姿态 动方程为[4 稳定.作用在目标航天器的控制力矩只是用来稳定 x=2w2+a., 自身的姿态,为最终平移段的接近创造条件,不直接 5=-wy+a, (1) 参与交会对接相对状态的机动;而追踪航天器以目 z=-a城+3w2z+a 标航天器为目标姿态(期望姿态),依据相对姿态反 方程(1)被称为H山方程或C-W方程.其中,在目标 馈进行姿态控制,实际上含有对目标航天器姿态定 轨道坐标系OgXoYoZ。中, 向偏差的补偿. La,a,a.]=F 假设目标航天器的稳定精度足够高,在整个的 mmm 最终逼近段,目标航天器的姿态四元数始终近似地 w=[0-w0]T,R=[00-R]T 为2=[1000]T.即目标轨道坐标系与惯性系 式中:ω为目标轨道坐标系O.X。YoZ。相对于惯性 重合 坐标系的转动角速度;当忽略重力和重力差影响的 控制的终端状态须满足无冲击对接条件: 时候,w=0;r、R分别为追踪航天器和目标航天器 (x,y,z,x,y,2)=(0,0,0,0,0,0) 相对地心的位矢;m为追踪航天器的质量,F.、F,、F: 在目标航天器轨道坐标系OgXoYoZ。中,如图 为追踪航天器推力分量,均为定值, 2所示,追踪航天器的位置矢量和速度矢量分别用? C F a 和户表示,r=[xyz],r=[y].在初始时刻, (2) r(0)=ro,(0)=i%,在时间t=T时刻,r(T)=Tr, r(T)=r,将r,指向r。的矢量定义为矢量p,即视

·532. 智能系统学报 第5卷 线距离,p(t)=r,-rr初始时刻p(O)=r。-rr=po, 推出 终点时刻p(T)=0,根据视线球坐标系与直角坐标 +a1元 (6) 系之间的转换关系(1)可以得到初始时刻、y%、0 的表达式: 由于1、z均有界,所以控制律(6)使到达运动稳 r0=PoC084.C0s8, 定的充分条件是控制力矩F应满足: yo=Pocos中,sin9, T.>mal=+2a121m} zo=-po8in也,. 式中:x|mr、Ia均为制导过程中各自量的最大 值,需要根据实际情况而定,同理,其他方向在控制 律(3)能够使到达运动稳定的充分条件为 日标航天器 T,>m kalylas lylm 实际路线 T.ma301 理论路线 4计算机仿真 4.1仿真条件 1)系统及状态参数 追踪航天器 r722 0 07 图2最终逼近段飞行轨迹 J= 0 8760, Fig.2 Flight path of final approach L O 0820 下面将设计基于H方程,视线轴接近模式的 0 直线型制导律. 50-1007 50 0 150 对于式(2),分别设定三轴的切换函数为 rSx=k(x-xa)+ka£, -100150 0- sy =kn(y -ya)+kny, (3) 起点视线距离:po=300.8m,末端视线距离:pa= 0,视线角:0,-35.26°,偏离角:4,=45°.将上述参数转 lsx=ku(z-zu)+k2乙 换到直角坐标系内位置初始值和位置末端值: 式中:k1k2、k1、k,2kka均为大于零的控制参数 x0=1732607,y=1732607,6=-1732326, 显然,上述切换函数所定义的滑模面是稳定的. x,=0,ya=0,2a=0. 另外,给定三轴的推力加速度的控制律为 初始线速度和末端线速度: r-A,5:>0; 0=-0.25m·81,y%=-0.25m·8, a={0, S:=0; 6=0.25m·81,4=0, 5:0时, 望值:[1000]';角速度的初始值:,= [0.10.10.1]'rad·s;期望值:=[00 &.=kae+ka主=ka正+ka(2ai-乙)<0. 0]Trad·s-l. (4) 2)控制参数位置781: 当s.<0时, A:=0.1m·s2(i分别代表x,y,z); 5.=k+khg(2oi0. k1=k1=k1=0.02,k2=k2=k2=5; m 推力器开机阀值:△1=0.03(i代表x,y,);推力器 (5) 关机阀值:△2=0.01(i代表x,y,z);姿态:um= 根据式(4)和(5),可以得到到达运动稳定的条 25N·m,入1=2=A3=3.5;k1=k12=k13=25,k= 件为 0.6. 4.2仿真结果及分析 m ,+20z T 图3为追踪航天器的线速度的变化曲线,可以
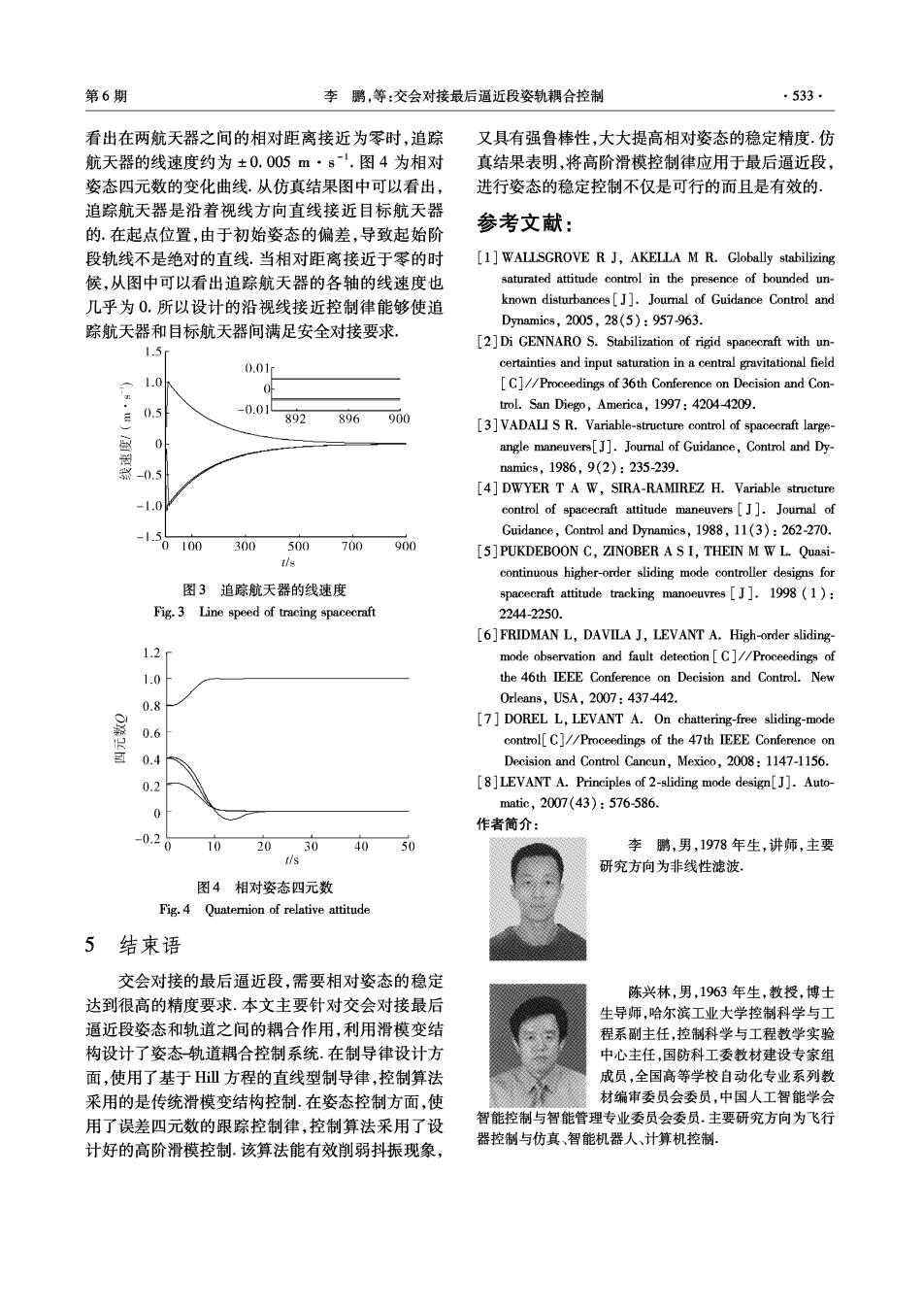
第6期 李鹏,等:交会对接最后逼近段姿轨耦合控制 ·533 看出在两航天器之间的相对距离接近为零时,追踪 又具有强鲁棒性,大大提高相对姿态的稳定精度.仿 航天器的线速度约为±0.005m·s.图4为相对 真结果表明,将高阶滑模控制律应用于最后逼近段, 姿态四元数的变化曲线.从仿真结果图中可以看出, 进行姿态的稳定控制不仅是可行的而且是有效的 追踪航天器是沿着视线方向直线接近目标航天器 的.在起点位置,由于初始姿态的偏差,导致起始阶 参考文献: 段轨线不是绝对的直线,当相对距离接近于零的时 [1]WALLSGROVE R J,AKELLA M R.Globally stabilizing 候,从图中可以看出追踪航天器的各轴的线速度也 saturated attitude control in the presence of bounded un- 几乎为O.所以设计的沿视线接近控制律能够使追 known disturbances [J].Journal of Guidance Control and 踪航天器和目标航天器间满足安全对接要求。 Dynamics,2005,28(5):957-963. [2]Di GENNARO S.Stabilization of rigid spacecraft with un- 1.5 0.01 certainties and input saturation in a central gravitational field 1.0 0 [C]//Proceedings of 36th Conference on Decision and Con- 0.5 -0.019 trol.San Diego,America,1997:4204-4209. 892 896 900 [3]VADALI S R.Variable-structure control of spacecraft large- angle maneuvers[J].Joural of Guidance,Control and Dy- -0.5 namics,1986,9(2):235-239. [4]DWYER T A W,SIRA-RAMIREZ H.Variable structure -1.0 control of spacecraft attitude maneuvers [J].Joumal of -1.5 Guidance,Control and Dynamics,1988.11(3):262-270. 0100 300500 700 900 [5]PUKDEBOON C,ZINOBER A S I,THEIN M W L.Quasi- tls continuous higher-order sliding mode controller designs for 图3追踪航天器的线速度 spacecraft attitude tracking manoeuvres J].1998(1): Fig.3 Line speed of tracing spacecraft 2244-2250. [6]FRIDMAN L,DAVILA J,LEVANT A.High-order sliding- 1.2 mode observation and fault detection C]//Proceedings of 1.0 the 46th IEEE Conference on Decision and Control.New 0.8 0lean8,USA,2007:437442. [7]DOREL L,LEVANT A.On chattering-free sliding-mode 0.6 control[C]//Proceedings of the 47th IEEE Conference on 0.4 Decision and Control Cancun,Mexico,2008:1147-1156. 0.2 [8]LEVANT A.Principles of 2-sliding mode design[J].Auto- matic,2007(43):576586. 作者简介: 0.20 10 20 30 40 50 李鹏,男,1978年生,讲师,主要 tis 研究方向为非线性滤波: 图4相对姿态四元数 Fig.4 Quaternion of relative attitude 5结束语 交会对接的最后逼近段,需要相对姿态的稳定 陈兴林,男,1963年生,教授,博士 达到很高的精度要求.本文主要针对交会对接最后 生导师,哈尔滨工业大学控制科学与工 逼近段姿态和轨道之间的耦合作用,利用滑模变结 程系副主任,控制科学与工程教学实验 构设计了姿态轨道耦合控制系统.在制导律设计方 中心主任,国防科工委教材建设专家组 面,使用了基于H方程的直线型制导律,控制算法 成员,全国高等学校自动化专业系列教 采用的是传统滑模变结构控制.在姿态控制方面,使 材编审委员会委员,中国人工智能学会 用了误差四元数的跟踪控制律,控制算法采用了设 智能控制与智能管理专业委员会委员.主要研究方向为飞行 器控制与仿真、智能机器人、计算机控制 计好的高阶滑模控制.该算法能有效削弱抖振现象