
第5卷第3期 智能系统学报 Vol.5 No.3 2010年6月 CAAI Transactions on Intelligent Systems Jun.2010 doi:10.3969/i.issn.1673-4785.2010.03.003 采用核聚类分析的KPCA改进算法 邓貌,陈旭,陈天翔,王徽蓉1,鲁华祥 (1.中国科学院半导体研究所,北京100083:2.厦门理工学院电子与电气工程系,福建厦门361005) 摘要:为了解决核主分量分析方法处理大训练样本集时计算代价巨大的问题,在采用子集划分的KP℃A算法基础 上,提出采用核聚类划分子集,并用每个子集的协方差矩阵的特征值累积贡献率作为标准来选取相应的特征向量. 分别在人工和实际数据集上测试,实验结果显示在同一累积贡献率和给定子集个数的条件下,采用核聚类划分子集 总能得到较小尺寸的核矩阵,而核矩阵尺寸的减小有助于改善测试样本的特征提取速度以及降低特征分解核矩阵 的时间复杂度. 关键词:核主分量分析:核聚类;子集划分;协方差矩阵;特征向量 中图分类号:TP18文献标识码:A文章编号:16734785(2010)03022106 Improved kernel principal component analysis based on a clustering algorithm DENG Mao',CHEN Xu',CHEN Tian-xiang,WANG Hui-rong,LU Hua-xiang (1.Institute of Semiconductors,Chinese Academy Sciences,Beijing 100083,China;2.Department of Electronic and Electrical Engi- neering,Xiamen University of Technology,Xiamen 361005,China) Abstract:To overcome the computational problems of the standard kernel principal component analysis (KPCA) algorithm,the authors proposed a new method for eigenvector selection by evaluating the cumulative contribution rate of the eigenvalues of the covariance matrix.In addition,a new way to partition the training data set based on kernel clustering was also developed.The influence was then explored of different partitions of training data sets on the size of the final kernel matrix,on the conditions causing a given cumulative contribution rate,and on the num- ber of subsets.Experimental results showed that a smaller kernel matrix can be obtained when kemel clustering method are used to partition the training dataset.The proposed algorithm can be helpful to reduce the time complex- ity of the eigen decomposition of a kernel matrix and to improve the speed of feature extraction for test samples. Keywords:KPCA;kemel clustering;partition of training data set;covariance matrix;eigenvector 核主分量分析(kernel principal component anal- 为此,文献[6]提出将训练集划分成若干子集, ysis,KPCA)通过Mercer核函数实现非线性映射,将 并将每个子集在特征空间中的协方差矩阵用一些特 主分量分析(principal component analysis,.PCA)方 征向量近似表示.基于这种近似表示,使KPCA在求 法在特征空间中推广.由于KPCA算法具有较强的 解过程中,只需对一个阶数等于这些特征向量数目 提取数据非线性特征的能力,因此它在模式识别、故 之和的核矩阵进行特征值分解即可,该方法简单有 障分析等领域得到了广泛的应用和重视1].但标 效,但是文中没有讨论每个子集应选取多少个特征 准KPCA算法需要对一个M×M的核矩阵(M为训 向量,以及训练集划分子集的不同方式是否会明显 练样本个数)进行特征值分解,当训练大样本集时, 影响最后选择的特征向量个数,从而影响分解最终 该方法面临计算代价巨大的问题。 核矩阵的时间复杂度以及求解测试样本的特征提取 时间.本文将针对这2个问题进行探讨. 收稿日期:2009-12-19. 基金项目:国家“863”计划资助项目(2007AA04Z423,2006AA01Z106):国 1基于子集划分的KPCA 家自然科学基金资助项目(60576033):福建省自然科学基金资 助项目(2008J04001);厦门市科技计划资助项目 (3502Z20083031). 由文献[6],设训练样本集X={x:1,划分的 通信作者:陈旭.E-mai:8 hendacx(@163.com

·222. 智能系统学报 第5卷 M个子集为Xk={x},k=1,2,…,M,N。为子集 块矩阵,K=AKA,为P:×P;的矩阵, X的样本个数,显然,有三X=X以及2N=N成 A=[aia…a], 立.经过非线性变换后,子集X,对应的特征点集为 a=[al…ag,al…a,…awl…aew], ={p(x)}兽1.记P的矩阵形式为 这样利用近似核矩阵飞就可以得到特征向量 p(X)=[p(xH)p(x2)…p(ra)…p(xw)], 对于测试样本z,它在特征向量”的投影为 k=1,2,…,M. M Pi 记训练样本集X=[x1x2…xw],子集X=[x1x2 ()(z)=】 i)(()- …w](k=1,2,…,M). (6) 对应地,把核矩阵K分成M×M块,即K= 喜 (K),i=1,2,…,M,j=1,2,…,M.其中:Kg= 式中:T=[k(xMz)k(xaz)…k(w,z)]. '(X)(X).记R=p(X)p'(X),则由KPCA 2基于核聚类分析的KPCA改进算法 算法原理 R=24()e(x) 由基于子集划分的KPCA算法6]可知,其关键 N台 M N 性能指标是=喜:V越小,既可使对丞特征分解 NA(xp()= 的复杂度O(3)降低:同时由于?的特征向量ā的 维数为N,若能减小N,则根据式(6)可知,可能改善 02x0p()=2风 测试样本的特征提取速度. 设A≥≥…≥为R的特征值,,吃,…,为 显然,影响N值大小的因素有子集个数M、每 对应的特征向量,则 个子集选取的特征向量个数P·另外,子集的不同 划分方式对N也有比较明显的影响。 R=)r=言” (1) 2.1特征向量的选取 式中:旷=√y=o(X),a为矩阵Ku的单位特 由基于子集划分的KPCA算法知,算法的关键 是用R、R。来近似R、Rk·对比式(1)和(2)可知,组 征向量,其对应特征值为入 成R.的Pk个特征向量与R,的N个特征值中最大 从R:的N。个特征值中选择最大的前Pk个特 的前P4个特征值入,A2,…,入相对应.提出采用特 征值,A,…,,使之满足: 征值的累计贡献率来确定Pk的值: M NE 设R的N个特征值为入,,…,入.记 令 S= 月,S(④=三娘 P =∑(), (2) 令R,前t个特征值的累积贡献率为 = Sz(t) 食=风对仅的 1 ()= (), (3) S. 给定一个比率r。,逐渐增加t直到某一个6,有 显然有≈R,R≈R,这样对R的特征值分解,就 y(t,)≥Ta,则Pk=t,即选择R的最大的前t,个特 可以近似地转换为对?的特征值分解.设入、°为? 征向量,然后利用式(2)和(3)可求得R和R: 的特征值和对应的特征向量,即有 2.2KKM划分子集 Rv=应 (4) 基于子集划分的KPCA算法需要将训练样本集 注意到,存在系数a5(k=1,2,…,M,j=1,2,…, 划分为若干子集.子集的不同划分方式会导致算法 P),使得 不同的性能,但文献[6]中并未讨论子集的划分方 M Pk 法.本文提出从聚类的角度出发,以距离为相似度准 .(5) 则把相似样本聚在一类,把每一类作为一个子集,以 将式(2)、(5)代入式(4),可得 此对训练样本集进行划分.又由于KPCA算法实际 Ka =Aa. 上是对训练样本经过核函数变换到特征空间中的特 式中:r=(rg)(i=1,2,…,M,j=1,2,…,M)为分 征点进行PCA分析,因此本文对这些特征点而非训

第3期 邓貌,等:采用核聚类分析的KPCA改进算法 ·223· 练样本聚类,即采用核聚类方法.典型的是核K-均 值(kernel K-means,KKM)聚类]: 3实验结果与分析 设训练样本集为X={x:}1,通过某种非线性 如上节所述,影响N值大小的因素包括子集个 映射中映射到某一特征空间H得到中(x,),中(x2), 数M、每个子集选取的特征向量个数P:以及子集的 …,(xw),{中()就是待聚类的样本核K-均 不同划分方式,若对子集的特征向量按照本文提出 值聚类算法实际上就是最小化目标函数 的累积贡献率选择选取,则Pk的值由给定的比率ra 决定.实验部分3.1节比较在相同的子集个数M、比 J=∑∑‖(x)-c2 率.的条件下,3种不同的划分子集方式(“一般” 式中:x为第i类的第j个样本,中(x:)是其在特征 划分、平分和核聚类划分)对N值的影响;实验3.2 空间中的投影,c:为第i类的中心 节给出以上3种划分子集的方式所对应的KPCA方 由=0,可得 法提取数据主要特征向量的实验结果.实验采用著 oc. 名的机器学习平台怀卡托智能分析环境(Waikato N 1∑(x), environment for knowledge analysis,WEKA)181, c:三N 常用软件如Matlab7.3等. 则对于某个给定的样本x,它在特征空间中与某类 3.1不同划分子集方式对N值的影响 中心c:的距离为 设有M个子集,一般的划分是子集元素个数N D=I-c2=Ie)-是2)- (k=1,2,…,M)为满足2N=N的任意一组数,本 N台 文称之为“一般”划分(general dividing),与之对应 - 2 + 的KPCA方法称为GDKPCA;如果划分到每个子集 = 的元素个数N.(k=1,2,…,M)基本相同(约为N/ M),本文称之为平分(equal dividing),对应的KPCA ,. 方法称为EDKPCA;本文提出的采用核聚类方法 由核函数定义: (kernel clustering)对训练集划分,聚类数目设为子 K(x,x)=, 集个数M,核聚类划分对应的KPCA方法称为KCK- D=K()-是Kx)+ PCA.将GDKPCA、EDKPCA和KCKPCA应用于人工 数据和实际数据,比较在相同的累积贡献率「。和核 参数条件下,这3种划分方式对最后特殊向量总数 值的影响.对每个数据绘制出不同子集划分对应 这样,就可以根据最近邻原则将每个样本分配给相 KPCA方法的N值随子集个数M变化的曲线,如图 应类别 1所示. -GDKPCA GDKPCA →年-GDKPCA …EDKPCA …EDKPCA ·EDKPCA 100r --KCKPCA 200r 300 --KCKPCA KCKPCA 50 「 200 z100 100--* 0 0 4.56 M810 02.54 4.5 6 10 (a)高斯混合数据 (b)环形数据 (c)于写体数据 图1不同的子集划分方式对特殊向量总数目的影响 Fig.1 The influences of different partitions of a subset on the size of eigenvector 图1(a)中的高斯混合数据(mixture data)由3累积贡献率r。=0.95,选用高斯核函数K,(x,y)= 个二维高斯分布数据点生成,各类的均值为 eml-y12,p1=2.5. (-0.5,-0.2)、(0.0,0.6)、(0.5,0.0),方差 图1(b)中的环形数据(ring data)由两类圆形 均为0.01,每一类产生500个点,共1500个样本 数据产生,每类由N=251个样本组成,共有样本
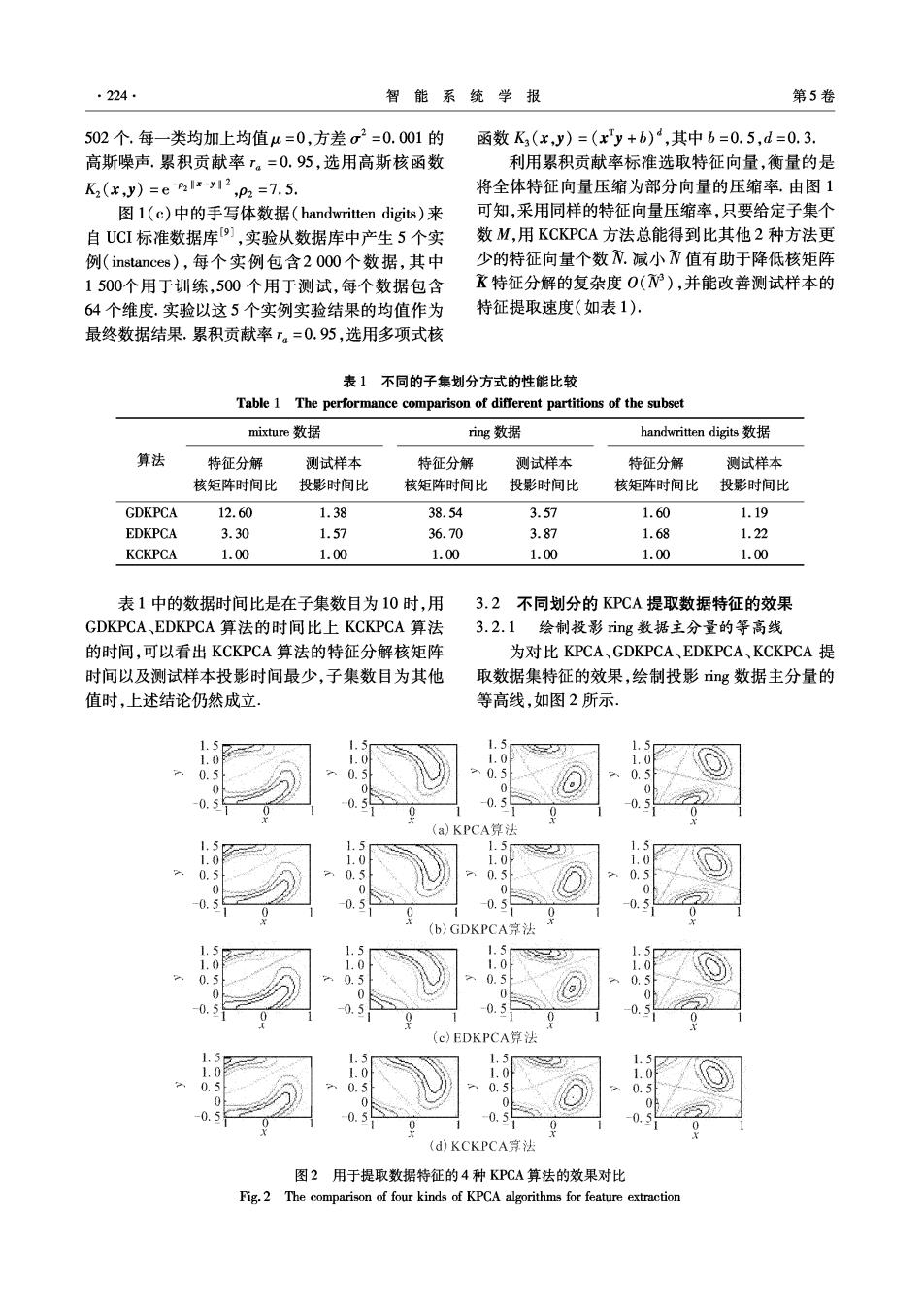
·224 智能系统学报 第5卷 502个.每一类均加上均值4=0,方差σ2=0.001的 函数K(x,y)=(xy+b),其中b=0.5,d=0.3. 高斯噪声,累积贡献率T。=0.95,选用高斯核函数 利用累积贡献率标准选取特征向量,衡量的是 K2(x,y)=em-y12p2=7.5. 将全体特征向量压缩为部分向量的压缩率.由图1 图1(c)中的手写体数据(handwritten digits)来 可知,采用同样的特征向量压缩率,只要给定子集个 自UCI标准数据库9),实验从数据库中产生5个实 数M,用KCKPCA方法总能得到比其他2种方法更 例(instances),每个实例包含2000个数据,其中 少的特征向量个数N.减小值有助于降低核矩阵 1500个用于训练,500个用于测试,每个数据包含 飞特征分解的复杂度O(3),并能改善测试样本的 64个维度.实验以这5个实例实验结果的均值作为 特征提取速度(如表1). 最终数据结果.累积贡献率r。=0.95,选用多项式核 表1不同的子集划分方式的性能比较 Table 1 The performance comparison of different partitions of the subset mixture数据 ing数据 handwritten digits数据 算法 特征分解 测试样本 特征分解 测试样本 特征分解 测试样本 核矩阵时间比 投影时间比 核矩阵时间比 投影时间比 核矩阵时间比 投影时间比 GDKPCA 12.60 1.38 38.54 3.57 1.60 1.19 EDKPCA 3.30 1.57 36.70 3.87 1.68 1.22 KCKPCA 1.00 1.00 1.00 1.00 1.00 1.00 表1中的数据时间比是在子集数目为10时,用 3.2不同划分的KPCA提取数据特征的效果 GDKPCA、EDKPCA算法的时间比上KCKPCA算法 3.2.1绘制投影ring数据主分量的等高线 的时间,可以看出KCKPCA算法的特征分解核矩阵 为对比KPCA、GDKPCA、EDKPCA、KCKPCA提 时间以及测试样本投影时间最少,子集数目为其他 取数据集特征的效果,绘制投影ring数据主分量的 值时,上述结论仍然成立, 等高线,如图2所示. 1.5 1.0 0.5 0 0 0.5 0. KPCA算 1.5 1.5 1.5 1.0 1.0 0. 0. 0 0 0.5 b)GDKPCA算法 1.5 1.0 0. 0.5 0 0 0.5 0 (c)EDKPCA第法 1.5 .0 0.5 0.5 0.5 0 0.5 (d)KCKPCA算法 图2用于提取数据特征的4种KP℃A算法的效果对比 Fig.2 The comparison of four kinds of KPCA algorithms for feature extraction

第3期 邓貌,等:采用核聚类分析的KPCA改进算法 ·225· 由图2可见,图中从上到下每一横排对应的 (GDKPCA、EDKPCA和KCKPCA)的效果和性能.首 KPCA算法分别为标准KPCA、GDKPCA(一般划 先用GDKPCA、EDKPCA、KCKPCA提取训练样本集 分)、EDKPCA(平分)、KCKPCA(核聚类划分);从左 的主要特征向量,然后将测试样本集投影到这些特 到右每一纵排分别对应按从大到小排列的前面4个 征向量方向上,得到特征提取后的测试样本集.在著 特征向量的投影图.图2中同一曲线上的点表示:在 名的机器学习平台WEKA上利用SMO(sequential 特征空间中,这些点在主轴方向的投影值相同,该曲 minimal optimization)分类器对特征提取后的测试样 线称为等高线.子集的特征向量选取按照累积贡献 本集进行识别.实验从数据库中产生5个实例(n- 率r。=0.95来选择.由图2可见,不同样本子集选 stances),每个实例包含2000个数据,其中1500个 择方法都能取得同标准KPCA算法基本相同的等高 用于训练,500个测试,每个数据包含64个维度.设 线,说明它们提取的数据集特征基本相同, 定各子集选择特征向量个数为10,需满足累积贡献 3.2.2UCI数据库handwritten digits识别 率r。=0.95,实验结果如表2所示 本实验的目的是比较3种基于样本子集方法 表23种方法(GDKPCA、EDKPCA和KCKPCA)的性能比较 Table 2 The performance comparison of three methods (GDKPCA,EDKPCA and KCKPCA) 方法 核矩阵尺寸 提取特征个数 测试误差率/% 样本投影时间比 GDKPCA 205 65 4.8 1.40 EDKPCA 203 64 5.0 1.42 KCKPCA 140 50 4.8 1.00 由表2可知,通过GDKPCA、EDKPCA和KCKP 具有十分重要的意义.本文在文献[6]中提出的基 CA3种变换后得到的新的测试集用于识别都能得 于子集划分的KPCA算法的基础上作了进一步的工 到比较准确的结果(测试误差率分别为4.8%, 作,具体地,提出了用核聚类方法来划分样本子集和 5.0%和4.8%).但同时注意到核聚类划分KP℃A 采用特征值累积贡献率来选择特征向量.实验验证 算法(KCKPCA)得到的核矩阵尺寸、提取特征个数 了核聚类方法的有效性、优越性和累积贡献率原则 和样本的投影时间均为最小,显示出一定的优越性. 的有效性.这种划分样本子集的方法和选择特征向 3.3实验结果分析 量的方式为应用KPCA方法进行非线性特征处理给 由以上实验结果可知,在实际应用中确定了划 出了新思路。 分子集的个数M以及选择子集特征向量的累积贡 但是,核聚类划分子集的KPCA方法仍有一些 献率r后,用核聚类划分子集的KPCA方法(KCKP 问题需要进一步研究.首先,需要在更多的、大量的 CA)能够得到与GDKPCA、EDKPCA基本相同的特 数据集上测试KCKPCA方法,以验证它是否具有普 征提取效果,但比GDKPCA、EDKPCA更能降低核矩 遍适用性.如果不能普遍适用,就需要分析它具有适 阵飞特征分解的复杂度O(3)以及改善测试样本 用性的条件以及最适合应用它的条件,其次,划分子 的特征提取速度, 集的个数M直接影响N值大小,是否能根据子集的 为了验证算法的稳定性,实验首先把数据产生 性质来估计较为合适的子集个数M,这个合适值又 多个实例,然后对每个实例分别测试,最后对这些实 应该怎样估计,另外,如何进一步改善测试阶段的特 例的实验结果求统计平均作为该数据的实验结果. 征提取速度等问题都需要进一步研究. 实验结果表明,KCKPCA方法相对于GDKPCA、ED- 参考文献: KPCA方法的优越性在测试数据集上是鲁棒的, [1]谢永华,陈伏兵,张生亮,杨静宇.融合小波变换与KP 结束语 CA的分块人脸特征抽取与识别算法[J].中国图象图形 学报,2007,12(4):666671 标准KPCA算法作为一种非常有效的非线性特 XIE Yonghua,CHEN Fubing,ZHANG Shengliang,YANG 征处理方法被广泛研究和应用,但是,当训练大样本 Jingyu.Features extraction and recognition of intersected 集时该方法面临的计算代价大的问题限制了它的进 human face based on wavelet transform and KPCA[J]. 一步应用.因此,研究如何改善大样本集的计算代价 Joumal of Image and Graphics,2007,12(4):666-671

·226. 智能系统学报 第5卷 [2]曾庆虎,邱静,刘冠军,谭晓栋.基于KPCA-HSMM设备 [8]The University of Waikaito.WEKA[EB/OL].[2009-12- 退化状态识别与故障预测方法研究[J].仪器仪表学报, 02].http://www.cs.waikato.ac.nz/ml/weka. 2009,30(7):1341-1346. [9]UCI.Semeion handwritten digit data set[EB/OL].[2009- ZENG Qinghu,QIU Jing,LIU Guanjun,TAN Xiaodong. 12-02].http://archive.ics.uci.edu/ml/datasets/Semeion Research on equipment degradation state recognition and Handwritten Digit. fault prognostics method based on KPCA-hidden semi-Mark- 作者简介: ov model [J].Chinese Journal of Scientific Instrument, 邓貌,男,1986年生,硕士研究 2009,30(7):1341-1346. 生,主要研究方向为优化算法、神经网 [3]LI Ying,LEI Xiaogang,BAI Bendu,ZHANG Yanning.In- 络、模式识别等. formation compression and speckle reduction for multifre- quency polarimetric SAR images based on kemel PCA[J]. Journal of Systems Engineering and Electronics,2008,19 (3):493498. [4]KIM K I,PARK S H,KIM H J.Kemel principal compo- 陈旭,女,1978年生,副研究员, nent analysis for texture classification[J].IEEE Signal Pro- 主要研究方向为图像处理、模式识别、 cessing Letters,2001,8(2):39-41. 神经网络等。 [5]ROSIPAL R,GIROLAMI M,TREJO L J,CICHOCKI A. Kemel PCA for feature extraction and denoising in non-line- ar regression[J].Neural Computing Applications,2001 10(3):231-243. [6]ZHENG Wenming,ZOU Cairong,ZHAO Li.An improved 陈天翔,男,1966年生,副研究员,主 algorithm for kemel principal component analysis[J].Neu- 要研究方向为神经网络、智能计算等。 ral Processing Letters,2005,22(1):49-56. [7]孔锐,张国宜,施泽生,等.基于核的K均值聚类[J].计 算机工程,2004,30(11):12-14. KONG Rui,ZHANG Guoxuan,SHI Zesheng,et al.Ker- nel-based K-means clustering[J].Computer Engineering, 2004,30(11):12-14. 全国图像图形学学术会议 The 15th National Conference on Image and Graphics(NCIG 2010) 第15届全国图像图形学学术会议(NCIG2010)将于2010年12月在广州召开.NCIG2010旨在为从事图像图 形相关领域的基础研究和应用推广的广大专家学者和工程技术人员提供一个相互交流的平台.会议将邀请国内 外著名的图像图形学领域的专家与会并做大会报告,邀请企业参加产品展示会.同时,将召开学会理事会, NCIG涵盖了计算机图形学、图像处理、视频通讯、虚拟现实、三维可视化、医学影像、数字艺术和游戏设计、机 器学习、信息安全等广泛领域. 会议将由清华大学出版社正式出版“会议论文集”,并且除在参会宣读的青年论文中评选优秀论文外,还将推 荐数十篇优秀论文到有关杂志上发表,欢迎踊跃投稿和参会交流, 会议网站:http:/ncig2010.gdut.edu.cn 电子邮件:ncig2010@gdut.edu.cn;ncig2010@163.com