
第5卷第2期 智能系统学报 Vol.56.2 2010年4月 CAAI Transactions on Intelligent Systems Apr.2010 doi:10.3969/i.issn.1673-4785.2010.02.006 一种机器人未知环境下动态目标跟踪 交互多模滤波算法 伍明,孙继银 (中国人民解放军第二炮兵工程学院计算机应用系,陕西西安710025) 摘要:为了解决机器人同时定位、地图构建和目标跟踪问题,提出了一种基于交互多模滤波(interacting multiple model filter,IMM)的方法.该方法将机器人状态、目标状态和环境特征状态作为整体来构成系统状态向量并利用全 关联扩展式卡尔曼滤波算法对系统状态进行估计,由此随着迭代估计的进行,系统各对象状态之间将产生足够的相 关性,这种相关性能够正确反映各对象状态估计间的依赖关系,因此提高了目标跟踪的准确性.该方法进一步和传 统的IMM滤波算法相结合,从而解决了目标运动模式未知性问题,IMM方法的采用使系统在完成目标追踪的同时 还能对其运动模态进行估计,进而提高了该算法对于机动目标的跟踪能力.仿真实验验证了该方法对机器人和目标 的运动轨迹以及目标运动模态进行估计的准确性和有效性. 关键词:IMM滤波;EKF滤波;同时定位;地图构建;目标跟踪;移动机器人 中图分类号:TP242.6文献标识码:A文章编号:16734785(2010)020127-12 An interacting multiple model filtering algorithm for mobile robots to improve tracking of moving objects in unknown environments WU Ming,SUN Ji-yin (Department of Computer,The Second Artillery Engineering College,Xi'an 710025,China) Abstract:A novel method was developed for synchronous localization and mapping (SLAM)and object tracking (OT)to provide simultaneous estimation of a robots and any objects trajectories in an unknown environment.The system was based on interacting multiple model (IMM)filtering.In this approach,the states of robots,objects and landmarks were used to form an integrated system state.A full covariance extended Kalman filter (EKF)was then employed to estimate system state.As the iterative estimation progressed,sufficient correlations between the differ- ent objects in the system could be establish to reflect the interdependent relationships of estimations between differ- ent system objects.In this way the precision of object state estimation was improved.Moreover,when combined with a traditional IMM filter algorithm,this method solved the uncertainty problem for modes of object motion.With the application of IMM,the method helped robots to track objects and estimate their modes of motion,improving the accuracy of object localization.Simulation results validated the effectiveness of the proposed method in the esti- mation of the trajectories of robots and objects and the modes of motion of tracked targets. Keywords:interacting multiple model filter;extended Kalman filter;simultaneous localization and mapping;object tracking;mobile robot 机器人同时定位与地图构建(SLAM)是指机器 程.SLAM的难度在于准确的地图构建依靠于准确 人在未知环境下,根据传感器信息迭代地完成环境 的机器人位姿估计,而准确的机器人位姿估计反过 地图构建,并同时对机器人位姿状态进行估计的过 来又依靠于准确的环境地图.对于这个“鸡生蛋,蛋 生鸡”的问题主要存在2类解决方法,其一是基于 收稿日期:200908-30. 通信作者:伍明.E-mail:hyacinth531@163.com 扫描点匹配的方法13],其二是基于Bayes估计的方

·128· 智能系统学报 第5卷 法,而基于Bayes估计的方法又主要分成基于扩展 x-1+4-△tcos(θ-+ys-1) 式卡尔曼滤波(EKF)的方法[4和基于粒子滤波的 yR-1+k-1△t8in(0瞻-+Yk-i) (1) 方法9).基于Bayes估计的SLAM解决方法的难点 0-l+(k-△t/B)·sin(yk-i) 在于对估计误差的正确处理,文献[10]已经对 SLAM误差产生的原因进行了分析 式中:△:为状态更新间隔,B为机器人轮毂长度,该 对于某些实际任务单凭传统的SLAM方法是无 轮式机器人模型符合非完整约束条件, 法解决的,例如:未知环境下目标跟踪任务,未知环境 1.2目标运动模型 下机器人围捕任务.这些任务要求将SLAM方法和目 目标在运动过程中一般并非保持惟一运动模 标跟踪方法相结合,该问题的难度集中于:如何在完 式,这里假设有2种可能的目标运动模型,即定速度 成未知环境下机器人定位任务的同时对未知运动模 模型(the constant velocity model,CVM)以及定加速 态的目标进行跟踪,并同时保证机器人和目标定位的 度模型(the constant acceleration model,CAM) 准确性.Wang等人21首先对该问题进行了研究并 首先定义CVM,假设目标在时刻k的状态由平 提出一种基于扫描点匹配的解决方法,由于该方法采 面笛卡尔坐标xCM和y以及在X、Y轴方向上 用的是最近点迭代(ICP)匹配算法,因此无法表示机 的速度M和M组成,即 器人和目标的不确定性.赵璇等3]提出了一种基于 XIVMCVM yICVMM yCVM] 粒子滤波解决方法,但该方法存在计算量大,以及地 则根据文献[2]介绍的方法可知目标CVM运动模 图长期一致性难以保证的问题4], 式预测函数为 本文提出了一种基于MM的机器人同时定位、 MM(M,AM)= 地图构建和目标跟踪(simultaneous localization and mapping witl汕object tracking,SLAMOT)方法.该方法 AX四Y+9. (2) 将传统的IMM目标追踪算法和基于EKF的SLAM 式中:41为状态转移矩阵,9为目标运动随机 算法相结合,完成了在未知环境下对机器人轨迹和 参量,其符合方差阵为Q的高斯白噪声, 目标轨迹的同时估计.仿真实验表明该方法对机器 对于CAM来说,目标的状态为xCW= 人轨迹、目标轨迹以及目标运动模态估计均较为准 [x4y“],其中和 确,并且由于系统所有状态向量均存在相关性,因此 A分别为目标在X、Y轴方向上的加速度,类似于 能够保证较好的地图长期一致性. CVM可以将CAM目标状态转移函数表示为 1机器人和目标的运动模型以及观测 MA(MAM) 模型 Ax4+9. (3) 式中:4为状态转移矩阵,q为目标运动随机 本节主要介绍系统所涉及到的相关运动模型以 参量,其符合方差阵为Q的高斯白噪声,限于篇 及观测模型,在机器人同时定位、地图构建和目标跟 幅,这里对这些参数的具体取值不予介绍,读者可参 踪过程中首先需要建立机器人和目标的运动模型, 见文献[2],图1显示了利用式(2)、(3)得到的目标 分别介绍如下 运行轨迹。 1.1机器人运动模型 18 CVM 设机器人状态为X=[xy],其中x、、 分别为k时刻机器人在全局坐标系下的平面笛卡尔坐 10 标以及相对于X轴的转角(标号上标表示描述对象,下 6 标表示时间).k-1=[k-1%-1]为k-1时刻机器人 2 的速度、角度控制量,“k-1存在均值为0、方差为Q的 0 -6 - 68 X/m 高斯噪声,则机器人运动模型如下: X=(X1,8-1,△t)= (a)CVM模态运行轨迹

第2期 伍明,等,一种机器人未知环境下动态目标跟踪交互多模滤波算法 ·129· 80 CAM 目标位置和 难点在于对于机器人状态和环境特征不确定性的刻 60 不确定范围 画上.因此对于机器人同时定位、地图构建和目标跟 目40 踪来说,其研究难点至少将是2个子问题难点之和. 20 下面给出基于IMM滤波的解决方法.算法总体流程 o 如图2所示. -20 -80 -60-40-20010 X/m 该算法主要包含2部分内容,其分别是基于 EKF的单模SLAMOT算法(图中对应Mode i EKF (b)CAM模态运行轨迹 方框),以及基于MM滤波的多模目标跟踪算法.需 图1目标CAM和CVM模态运行轨迹图 Fig.1 The tracks of object in CVM and CAM model 要说明的是,整个算法是在MM框架下进行的,而 图1中2幅子图分别显示了目标以CVM和 基于EKF的单模SLAMOT算法是为了完成不同系 CAM运行时的轨迹,从该图可见,当目标以CAM运 统状态的预测和更新而设计的.具体来说,每当系 动时,无论其实际运动范围,还是位置不确定范围, 统获得环境规测值,将利用这些观测值对不同目标 均大于以CVM运动的结果.由此说明,CAM适合描 运动模态对应的系统状态分别进行更新,进而得到 述运动不确定性较大的目标,而CVM则适合描述运 不同的系统状态向量和协方差阵更新值和P, 动不确定性小的目标. 在此基础上,运用MM方法得到本次迭代最终的系 1.3特征、目标观测模型 统状态和协方差阵X。和Pk,以下对整个过程进行 假设特征lm的状态为其笛卡尔坐标,即X= 详细介绍。 [xy]T.观测量为距离和方向信息,即z= 状态估计 4,i 协方差组 [dy]I,则系统对目标T和特征lm:的观测函数分 合产生 别为 XiPv zi=[diye]=h(XK,Xi,R)= Mode 1 EKR 「√(-)2+(y-) ,P…i 模式概 +R (4) 更新 环境 Mode 2 EKF 观测值 和 XiPiVi 数据交互 i=[dim yim ]=hM (XR,X,Rim)= Mode s EKF X √(0-)2+(y-y) Xupe.Vi +Rm.(5) 图2 SLAMOTIMM滤波算法流程图 Fig.2 The flow chart of SLAMOTIMM algorithm 式中:X、X分别为机器人和目标的状态量,R是 2.1状态向量的表示 均值为0,协方差为diag(q,q)的观测噪声. 首先介绍系统状态的设置,这里将系统状态表 示成机器人状态、目标状态和环境特征状态组合的 2 基于IMM的机器人同时定位、地图 形式,即 构建和运动目标跟踪方法 X= (6) 目标跟踪和机器人SLAM研究的重点各有不 LLM: 同,例如,对于目标跟踪来讲研究的难点一般在于对 式中:X=[y]为机器人k时刻的状态值, 目标运动模型的未知性上,而机器人SLAM研究的

130. 智能系统学报 第5卷 指出的是系统最初的向量只包括机器人状态,而 为目标k时刻的状态值;LM= : 为当前已发现 目标状态X和环境特征状态LM是在机器人取得 特定观测值后逐步扩充进来的, 环境特征状态的组合(其中X:=[y]).需要 相应地,该系统的协方差阵具有如下形式: C(Ri,R:) C(R:,T) C(Rk,m1)… C(R:,Im)7 C(T,R) C(T,T) C(Tk,lm1)…C(Tk,lmn) P= C(m1,R)C(lm1,T) C(lm1,lm1)…C(lm1,lmn) (7) -C(Im,R)C(Im,Tx) C(Im ,Im)...C(Im,Im 为了形象起见,这里用Rk表示,Tk表示X, Xo=converse(X,z) 1m:表示X,C(A,B)代表A和B的协方差阵,由 x+dcos(y+)1 (9) 式(7)可知,该系统主要存在6种相互依赖关系,其 y+sin( 分别是:机器人自身之间的依赖关系C(R,R),目 这里假设对于目标和新环境特征的观测值分别 标自身之间的依赖关系C(Tk,T),环境特征自身 为z和z,由于该逆推函数只能提供对象的笛卡 之间的依赖关系C(m:,m:),机器人和目标之间的 尔坐标信息,因此式(8)中只得到目标状态X的前 依赖关系C(R,T),机器人和环境特征之间的依赖 2项.下面分别说明对Xt和X的扩展方法. 关系C(R,m),目标和环境特征之间的依赖关系 1)针对目标状态扩展.假设系统状态向量已经 C(T,m:),不同环境特征之间的依赖关系 包括n个特征向量(不包括特征的情况类似),则当 C(m,m),i≠i 得到目标X时扩展方法如下: 2.2EKF形式的SLAMOT解决 X 本节介绍如何用EKF来解决SLAMOT问题,其 X 主要分为:扩充阶段(augment)、预测阶段(predict)、 augment(,X): (10) 更新阶段(update). 2.2.1扩充阶段 初始阶段系统的状态向量只包括,在运行过 度前 扩恶后 程中,当第一次得到对于目标的观测值或新环境特 从上式可见目标状态子向量紧跟着机器人状态 征的观测值后系统将对状态向量和协方差阵进行扩 子向量。 展,本节介绍具体方法 2)针对新特征状态扩展假设系统状态向量已经 首先介绍对于状态向量的扩展.式(4)、(5)给 包括n个特征向量和目标状态向量(不包括特征的情 出了对于目标和环境特征的观测函数,这里可以得 况类似),则当得到新特征Xm时扩展方法如下: 到其逆推形式如下,即已知X和z:条件下如何得 X 到X和Xe, g X=converse()= XI X 「x+dcos(y+) augment(Xk,Xao): y y+di sin(y+o) Xie 0 0 (8) 守度前 .· 扩展后 0 (11)

第2期 伍明,等,一种机器人未知环境下动态目标跟踪交互多模滤波算法 ·131· 此时系统的已知特征数量为n+1. 1)针对目标的系统协方差阵扩展.假设系统状 在对系统状态向量完成扩展后还须对系统协方 态向量已经包括n个特征向量(不包括特征的情况 差阵P.进行扩展,同样分别对目标和新特征分别进 类似),则针对目标T系统协方差阵扩展方法如下. 行说明. C(R,R:) C(Rk,m1) C(Rx,Im,) C(m1,R)C(lm1,lm1)…C(lm1,lmn) augment(P:,CE.g,CE:): C(mn,Rs)C(mn,m1)…C(mn,lmn) 扩展前 C(Rx,R) C(Rk,T)C(Rk,lm1)… C(Rk,lmn) C(T:,R) C(Tk,T)C(Tk,lm)… C(T,Im,) C(m1,R)C(lm1T)C(lm1,lm1)…C(lm1,lmn)) (12) C(Im,R)C(Im,T)C(Im,Im)..C(Im,Im)- 扩展后 式中 CE= converse() C(T,R)=(C(R,T.))=CExgC(Rx,R), z (13) cos(0+y)-di sin(+) (17) C(T:,T:)=CExC(R:,R:)(CExs)T sin(0+) d话cos(0瞻+y) CE:R"(CE:t)", (14) 式(16)、(17)分别为式(8)对机器人状态X和目 C(T:,Im;)=(C(Imi,T:))= 标规测值z的雅可比阵,式(13)~(15)分别由误 CExgC(Rx,Im;),i=1,2,...n (15) 差传播公式得到. a converse() 2)针对新发现目标的系统协方差阵扩展.这里 OXR 假设此时系统状态向量已经包括目标状态和n个特 [1 0 -d sin(0+) 征状态(不包含的情况可以类似得到),以下用m+ Lo 1 (16) di cos() 代表新发现的特征,那么系统协方差阵扩展如下, C(R:,R:)C(R:,T:)C(R:,Im).C(R:,Im,) C(Tx,R) C(Tk,Tk)C(Tk,lm1)…C(Tk,lmn) augment(P:,CExg,CE): C(Im,R:)C(Im,Tx)C(im,Im)..C(Im,Im) -C(mn,Rg)C(lmn,Tk)C(lmn,lm)…C(mn,lmn) 扩展前 C(R,R) C(Rx,Tx) C(R,1m1) C(RIm C(Rk,lma+i) C(T,Rx) C(Ti,T) C(Tk,1m1)… C(T&,Im,) C(Tx,Im) C(Im,Rx) C(m1,T)C(lm1,lm1)… C(lm1,lmn) C(lm1,lm+l) (18) C(Im,Rx) C(Im,,T:)C(Im,,Im) C(Im.Im. C(Im,Im) C(lml,Rs)C(m+1,T)C(m+1,m1)…C(m+1,m,)C(ml,mi) 扩展后

·132· 智能系统学报 第5卷 式中: X山k=产(X发,△t,4是+). (25) C(m+1,R)=(C(R,lmn+1))T= 同样将根据完成对目标状态子向量的预测,即 CExgC(R:,R:), (19) X=f(X,ARu,g). (26) C(Im,T)=(C(T,Im))= 因此经过系统状态预测后,系统的状态向量变化如下: CExgC(Rx,Tx), (20) X-=StatePredict(X:,,At,Aiu,)= C(Im,Im)=(C(Im,,Im))= Xk 「严(X装,△t,4数+k) CExgC(Rx,Im),i=1,2,.n, (21) Xi-uk f(X,A4k,9) (27) C(Im,Im)CExgC(R:,R.)(CExg)T+ LMk-uk LMLM CER(CE)T, (22) 2)系统协方差预测.协方差预测实际上可以理 converse() 解为一种不确定性传播过程,机器人和目标在状态 OXR 预测后不确定性也应相应传播扩大.这种传播扩大 [10-dsin(眼+yo) 不仅体现在机器人和目标本身的协方差子阵上 (23) L0 1 cos(08 +) (C(Rk,R)和C(Tk,T),也应体现在机器人和目 dconverse(X,zo) 标之间(C(R,T)、机器人和特征之间(C(R, CEme= mw 1m))以及目标和特征之间(C(Tk,1m))的协方差 cos(狼+y)-dsin(眼+ym)1 子阵上,以下分别介绍. sin(+y)dcos(6g+y) 对于机器人自身协方差子阵预测利用误差传播 公式可得 (24) C(Rk+k,R+I)= 式(23)、(24)分别为式(9)对机器人状态X FC(R:,R:)(F)+FF), 和特征观测值的雅可比阵,式(19)~(21)同 (28) 样由误差传播公式得到. 2.2.2状态预测阶段 r10-△tsin(0+Ys) 在SLAM0T过程中主要存在2个运动物体,其 F路= ax=01 v△tcos(瞻+Y) 分别是机器人和目标,状态预测阶段的任务就是利 L00 1 用两者的运动模型对其状态和系统协方差阵进行预 (29) 测.一般来说,作为观测主体的机器人其运动模型是 确定的,而作为观测对象的目标其运动模型并不确 定,本节假设已知机器人和目标的运动状态,后面章 △tcos(瞻+ya)-x△tsin(+a)T 节将考虑多模态情况下的应用. △tsin(0+yk) v△tsin(0+Ye) (30) 这里采用式(1)作为机器人的运动模型,记 △t&in(yz)/B △tcos(Ya)/B 为,目标的运动模型为式(2)和式(3)之一,记为 式中:C(Rk+k,Rk+)代表机器人预测协方差子阵 ∫.预测阶段包括:系统状态预测和系统协方差预 的值,Q代表机器人控制输入的误差阵,Fg、F 测2部分,分别介绍如下. 分别为式(1)对机器人状态X和机器人控制向量 1)系统状态预测.由于特征分布是固定不变 的雅可比阵。 的,因此系统状态预测操作的对象是式(6)表示的 类似地,对于目标自身协方差子阵预测值为 系统状态X,的前2项,即机器人状态子向量X和 C(TT)=AIC(T,T)(AI)+k 目标状态子向量X.这里将根据“得到预测后的 (31) 机器人状态子向量+为 式中:C(Tk+k,T+1k)代表预测后目标协方差子阵

第2期 伍明,等,一种机器人未知环境下动态目标跟踪交互多模滤波算法 ·133· 的值,A红+为目标运动模型状态转移阵,Q+1k为状 FRgC(R:,T)(AI). 态误差阵。 同样,机器人与特征1目标与特征的协方差子阵 机器人和目标之间协方差子阵预测值为 预测值分别为 C(R,T)=FxgC(R,T)(AI).(32) C(Rk-uk,Im)=FxgC(R:,Im:), (33) 其推导如下: C(Tk-uk,Im:)AtC(R&,Im;). (34) 因为C(R+k,T)=FC(R,T), (I) 综上所述,最终系统协方差阵变换如下, C(R,T)=C(R,T:)(AI),(I) 所以由式(I)、(Ⅱ)可得:C(R+k,Tk+k)= P=ConvariancePredict(P:",At,A)= C(Rs+k,Rs+e)C(Rk+k,Ts+)C(Rk+nk,lm1)…C(Rk+Hk,lmn) C(T4k,R4k)C(Tk4k,Tk+)C(Tk+k,m)… C(Tk+k,lmn) C(Im1,Rg+uk) C(m1,Tk+) C(Im,Im) C(Im,Im) (35) C(Im ,R+uk) C(Im,Tx-uk) C(Im,Im) C(lmn,lmn)J 2.2.3更新阶段 Hit 当观测值出现时,EKF将对系统状态向量和协 方差阵进行更新从而纠正系统的误差.这里假设已 Hk+1= (36) 经完成数据关联工作,即已知观测值和目标、特征的 HT 对应关系.设观测值分为对于目标的观测值z+和 式中:H!和H为2×dim(Xk+)的矩阵,Hg+1为 对于特征的观测值z1,i=1,…,m+1(m+1为此次 目标状态子向量+和机器人状态子向量+1k 观测到的特征数量)2部分组成。 对应目标观测值z的观测矩阵.其值为 下面首先需要建立此次系统的观测矩阵Hk+1, 该矩阵形式如式(36): H4= h LaXklke aXu6 02x (37) ”2x(9+2n) 式中: x处-x 发E-yE dhr √(k-x)+(y4a-y √(+s-x)+(4k-4) aXi-u 38) - 是一e √(4+k-经)2+(yt-y2了 √(+t-4)+(y4k-y发)了 - yiu-yhcu ohT √(k-)+(g+k-) V(k-发+)'+(a-么4了 aXuk 02x yheu -yict k一 √(s-xe)+(y-发e)了 √(k-+e)+(yk-发E了 (39) 式(38)、(39)分别为式(4)对于X1和X+的雅 假设每个观测值,与系统状态变量中特征的 可比阵。 对应关系已经确定,即,z对应系统状态向量中的

·134 智能系统学报 第5卷 特征为,也就是说,对应系统状态向量X中的 X元素.则Huk为 oh LM 0 ohLM aX4ae 0… (40) 第9+2×所,列到0+2×+1) 2×(9+2m k- ykeu -yeu 0 8hLM √(x-塔)+(3-)了 √(-)+(0-)户 aXuk (41) yo-yu 是-好5 √(x-+)产+(-+)了 √(2-)'+(2-y4) 18 yi-yu ihLA √(-x)+(0-y) √(-+)2+(-y+) X (42) 喔- 0-x √(-)+(-y) √(-x4e)2+(-yg)产 式(41)、(42)分别为式(5)对于X和X的雅 将式(44)、(45)代人式(43)就可求出观测差异向 可比阵。 量V+ 接下来还需确定观测差异向量,所谓观测差异 在得到系统观测矩阵H+1和观测差异向量 向量是指:预测到的观测值和实际观测值的差异,这 ”k+基础上,对系统状态向量和协方差阵进行更新, 里记为 过程如下: -Z Xk+k+1=X6+E+Kk+1'+1, (46) - P++=Px+uk -K+IS(K).(47) Vkel (43) 式中:K+1=Pk+k(H+1)(S+1w)-为卡尔曼增 Lv z1一z使 益,ISk+=H+P+(H&+i)T+R+Ik为此刻系统 式中:z+,对于目标和特征的预测观测值, 观测协方差阵,R+1k为观测噪声阵。 2.3基于MM的SLAMOT解决方法 z+1,代表实际观测值,+代表对于目标的观测 正如前面所述,目标跟踪问题难点在于目标运 差异,代表对于特征的观测差异。 动模型的不确定性,为了解决这个问题,下面给出基 z为目标预测观测值,根据式(4),可得: 于MM的解决方法, √(x+k-x+z)+(y+-y+) MM滤波器[1)是计算效率较高的次优状态估 计算法,其主要用于对马尔可夫切换系统(Mark arctan( yk+ulk -y+uk ovian switching systems)的估计问题.如图2所示, (44) IMM滤波过程主要分为3个部分:数据交互(inter- 设已知特征预测观测值z对应系统状态向 action)、各模态滤波(filtering)和状态组合(combina- 量中的特征引索为,则有: tion).下面给出发现目标后一次循环的处理过程: √(-x4)+(-) 1)数据交互过程.首先对于Hi,j∈M计算混合 Z= 概率值=(1/c)pi-1,其中c为归一化因数,其 arctan( )-… 值为9=王pu-…之后对于HjeM计算初始状态 (45) 和协方差阵,即

第2期 伍明,等,一种机器人未知环境下动态目标跟踪交互多模滤波算法 ·135· Xg=∑X, (48) 行即可 P=∑{P+[X-g]×[X-g]T}u, 3仿真实验结果 (49) 下面将通过仿真实验来验证该方法的有效性, 2)不同模态状态预测阶段.对于目标运动不同 实验是在Matlab7.5下进行.为了能够体现机器人 模态T∈M,根据式(27)、(35)完成各模态对应系 机动性的特点,这里设计控制律使得机器人能够跟 统状态向量和协方差阵的预测: 随目标运动.具体来说,首先计算机器人位置和目标 X=StatePredict(X,u,At,A), 位置的角度,以此作为机器人角度控制量,之后计算 (50) 机器人位置和目标位置的距离,以此作为机器人速 Pux=CovariancePredict 度控制量,这里设置了几个速度标准并根据距离的 (P,Xg,u袋k,2,△t,A24,Quk).(51) 远近来选择不同的速度标准 若有观测值出现继续,否则转到6). 目标在不同时段分别采用定速度模型和定加速 3)不同模态状态更新阶段.利用式(46)、(47) 度模型2种不同运动模式,该实验首先在长度为 完成不同模态系统状态和协方差阵的更新 -250~250m,宽度为-250~250m的正方形区域 +山+1=区+k+K区+11, (52) 内均匀产生800个特征点.为了更准确地分析结果, P++1=P+k-K+IS2+(K+1)T.(53) 假设运动开始时机器人就发现了目标,机器人的运 4)模式概率更新.不同于传统的MM,此处 动控制误差阵为Q=diag(12m,0.252rad),机器人 的取值只考虑目标观测值可能性并不考虑特征观测 观测误差为R·=diag(0.12m,0.052rad)机器人的 值可能性,因此=N((1:2);0,IS(1:2,1: 观测视野为前向,观测最大距离为100m.目标在定 2)),(1:2)表示取的前2项(对应目标观测值 速度模型下的噪声变量gcM=0.1,在定加速度模 差异),IS(1:2,1:2)表示取IS的1~2行和1~ 型下的噪声变量g心“=1.8,每一轮迭代的间隔时 2列子阵(对应目标观测协方差子阵).之后对于各 间为△t=0.158,仿真共进行200次迭代.所得到的 模式计算本次更新后的模式可能性,即 结果如图3所示.图3显示了实验的总体情况,其中 4=(1/c)∑p1=(1/c)9(54) 虚线和实线分别表示目标的实际和估计轨迹;虚线 和实线分别表示机器人的实际和估计轨迹;带星号 式中:c为归一化因数. 5)系统扩充.当存在对于新特征的观测值时, 三角代表已发现标志的概率分布,其中星号代表分 根据式(11)完成状态向量的扩充,式(18)完成协方 布均值,三角代表不确定性三角;星号代表特征的实 差阵的扩充, 际位置.机器人和目标的起始位置为(0,0),机器人 6)系统状态估计,协方差阵组合产生.最终通 的终点为(97,2.65),目标的终点为 过加权得到本次迭代的系统状态估计和协方差阵, (101.1,-3.68).从图中看出机器人为了追赶目标 计算方法如下. 出现了几次环型运动. 一机器人估计运动轨迹 X41=∑4lk+4, (55) 40 ··一一机器人实标运动轨迹 20: 机器人。“ 日标估计运动轨迹 日标实际运动轨迹 Pe=∑{P+k+l+ 0 入特征估计分布 -20 自标 ·特征实际位置 [Xnk41-Xe]×[及+k+1-X]T{A.(56) -40 以上算法过程假设目标已经出现,如果目标没 -60 020020406080100 有出现,那么系统将按照传统EKF_SLAM的方法运 X/m 行,当发现目标后首先利用式(10)、(12)对系统状 图3仿真总体图 态向量和协方差阵进行扩充,之后按照上述方法运 Fig.3 Simulation results of SLAMTO
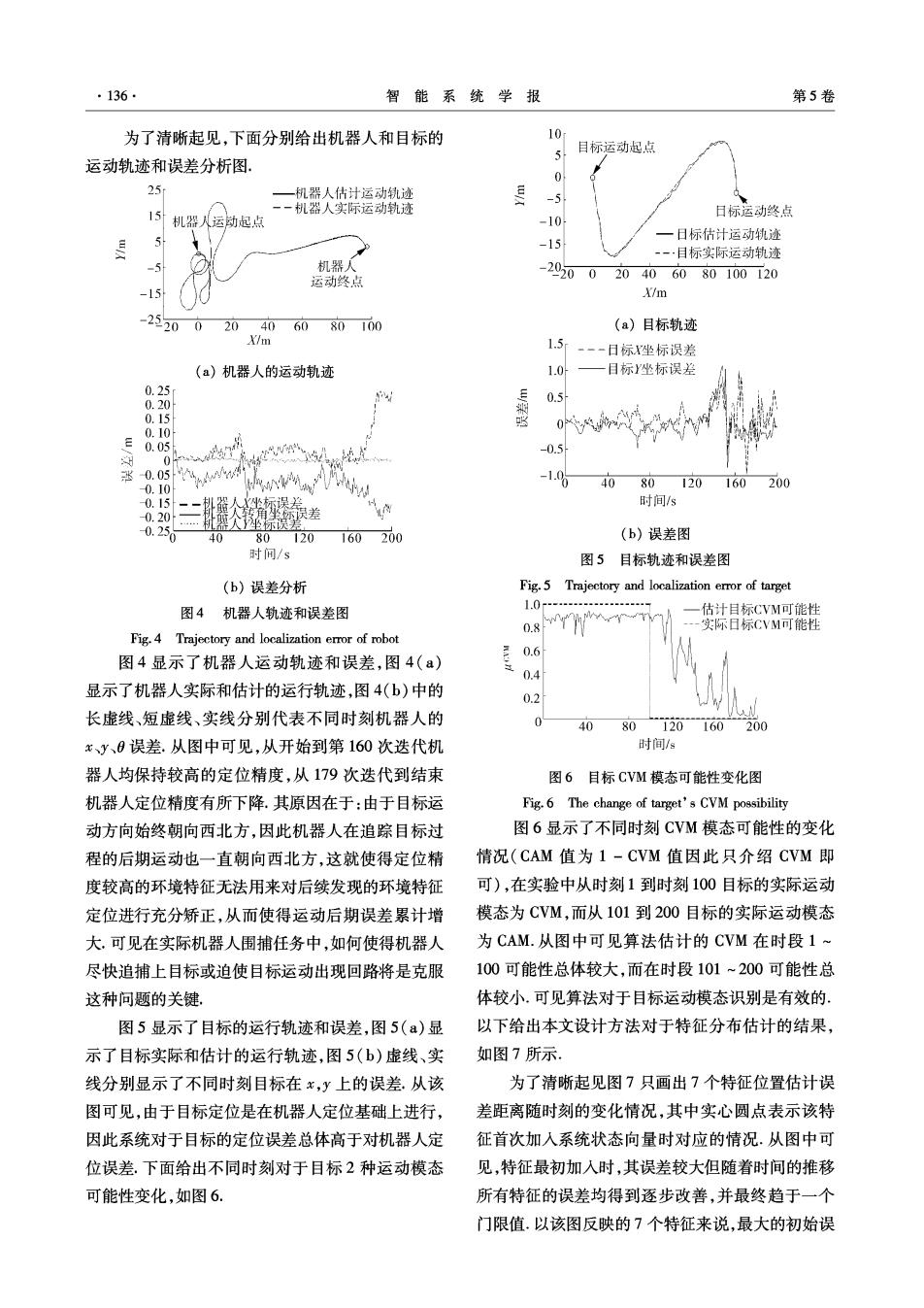
·136 智能系统学报 第5卷 为了清晰起见,下面分别给出机器人和目标的 10 目标运动起,点 运动轨迹和误差分析图, 25 一机器人估计运动轨迹 -5 一一机器人实际运动轨迹 15机器人运动起点 日标运动终点 -10 一日标估计运动轨迹 -15 -·目标实际运动轨迹 机器 运动终点 -2020020406080100120 -15 X/m -25200 20406080100 (a)目标轨迹 X/m 1.5 一一-日标X坐标误差 (a)机器人的运动轨迹 1.0 目标Y坐标误差 0.25 E 0.5 0.20 0.15 0.10 0 0. 0w -0.5 -0.0 10 0.10 40 80120 160 200 0.15 机器人坐标误差 时间/s 0.20 0.25 一人速差 40 80120 160200 (b)误差图 时问/s 图5目标轨迹和误差图 (b)误差分析 Fig.5 Trajectory and localization error of target 图4机器人轨迹和误差图 1.0- 估计目标CVM可能性 -实际日标CVM可能性 Fig.4 Trajectory and localization error of robot 0.6 图4显示了机器人运动轨迹和误差,图4(a) 0.4 显示了机器人实际和估计的运行轨迹,图4(b)中的 0.2 长虚线、短虚线、实线分别代表不同时刻机器人的 40 80120160200 x、y、9误差.从图中可见,从开始到第160次迭代机 时间/s 器人均保持较高的定位精度,从179次迭代到结束 图6目标CVM模态可能性变化图 机器人定位精度有所下降.其原因在于:由于目标运 Fig.6 The change of target's CVM possibility 动方向始终朝向西北方,因此机器人在追踪目标过 图6显示了不同时刻CVM模态可能性的变化 程的后期运动也一直朝向西北方,这就使得定位精 情况(CAM值为1-CVM值因此只介绍CVM即 度较高的环境特征无法用来对后续发现的环境特征 可),在实验中从时刻1到时刻100目标的实际运动 定位进行充分矫正,从而使得运动后期误差累计增 模态为CVM,而从101到200目标的实际运动模态 大.可见在实际机器人围捕任务中,如何使得机器人 为CAM.从图中可见算法估计的CVM在时段1~ 尽快追捕上目标或迫使目标运动出现回路将是克服 100可能性总体较大,而在时段101~200可能性总 这种问题的关键, 体较小.可见算法对于目标运动模态识别是有效的。 图5显示了目标的运行轨迹和误差,图5(a)显 以下给出本文设计方法对于特征分布估计的结果, 示了目标实际和估计的运行轨迹,图5(b)虚线、实 如图7所示. 线分别显示了不同时刻目标在x,y上的误差从该 为了清晰起见图7只画出7个特征位置估计误 图可见,由于目标定位是在机器人定位基础上进行, 差距离随时刻的变化情况,其中实心圆点表示该特 因此系统对于目标的定位误差总体高于对机器人定 征首次加入系统状态向量时对应的情况.从图中可 位误差.下面给出不同时刻对于目标2种运动模态 见,特征最初加人时,其误差较大但随着时间的推移 可能性变化,如图6. 所有特征的误差均得到逐步改善,并最终趋于一个 门限值.以该图反映的7个特征来说,最大的初始误