
第5卷第5期 智能系统学报 Vol.5 No.5 2010年10月 CAAI Transactions on Intelligent Systems 0ct.2010 doi:10.3969/i.issn.1673-4785.2010.05.011 改进粒子群算法的潜器导航规划 唐小勇,于飞,潘洪悦 (哈尔滨工程大学理学院,黑龙江哈尔滨150001)】 摘要:针对粒子群算法的寻优搜索能力强和已有的一些导航算法存在收敛速度慢、迭代时间长的缺点,提出一种 基于粒子群算法的潜器导航算法.利用群智能理论,对基本粒子群算法进行改进:提出一个含突变因子的可变调的 惯性权值策略,从而达到增强粒子群算法局部和全局寻优的调度能力.通过实验仿真验证,证明了改进粒子群算法 具有更优的性能.在此基础上,将该算法应用到水下潜器的路径规划中,通过对环境的建模分析进行条件约束,最终 将路径规划问题转化为路径点求解的优化问题.实验仿真结果获得了从起点到终点的无碰撞路径,收敛速度也较 快,验证了该方法的有效性和可行性. 关键词:潜器导航:路径规划:粒子群算法 中图分类号:1P242.6文献标识码:A文章编号:1673-4785(2010)05044306 Submersible path-planning based on an improved PSO TANG Xiao-yong,YU Fei,PAN Hong-yue (College of Science,Harbin Engineering University,Harbin 150001,China) Abstract:To overcome the shortcomings in slow convergence speed and long iteration time in the existing algo- rithms,take advantage of the searching ability of a particle swarm optimization(PSO),a new navigation algorithm was created based on PSO.First,the theory of swarm intelligence was used to improve the basic PSO algorithm: proposing a transformable inertia weight which contains a mutation factor to improve the PSO,and thereby enhan- cing the local and global optimum capability of PSO.Through experimental simulation and validation,the better performance of the improved PSO (IPSO)was proven.On this basis,the IPSO was used in path planning of an un- derwater vehicle.By using modeling analysis of space and adding constraint conditions,the path planning problem was converted into an optimization problem concerning solutions of path points.Finally,through experimental simu- lation,a collision-free path from start to finish was given,proving the validity and feasibility of this method. Keywords:submarine navigation;path-planning;particle swarm optimization 导航规划是潜器智能化航行的关键技术之一.潜遗传算法、神经网络算法等24,虽然这些算法都有其 器的导航规划分为静态环境下的导航规划和动态环 自身的优点,但同时也存在一定的局限性,因此,根据 境下的导航规划.其中,静态环境下的导航规划需要 不同的环境信息和性能指标选取不同的算法是提高 在规划前获得完整的环境信息,目前静态环境下的导 导航规划能力的有效途径.另外,在导航规划的建模 航规划有许多解决方法,如人工势场法、可视图法等, 方面已有很多方法56],本文在已有建模方法的基础 这些都得到了广泛应用];而动态规划不仅要事先得 上提出一种更为简捷的导航规划方法,并结合改进的 知一些情况,还必须有及的时突发事件处理系统,在 粒子群优化算法,获得全局最优路径 理论和计算上相对比较复杂,必须具体问题具体分 1标准粒子群算法及其改进 析,目前成型的算法较少.近年来,随着智能算法的发 展,许多智能算法也被应用到潜器的导航规划中,如 1.1标准粒子群算法 粒子群算法(PSO)是由Eberhart和Kennedy于 收稿日期:2009-0305 基金项目:国家自然科学基金资助项目(60704001). 1995年提出的基于群体智能行为的一种进化算 通信作者:唐小勇.E-mail:y_201@163.com 法).在粒子群算法中,每个优化问题的解都是搜
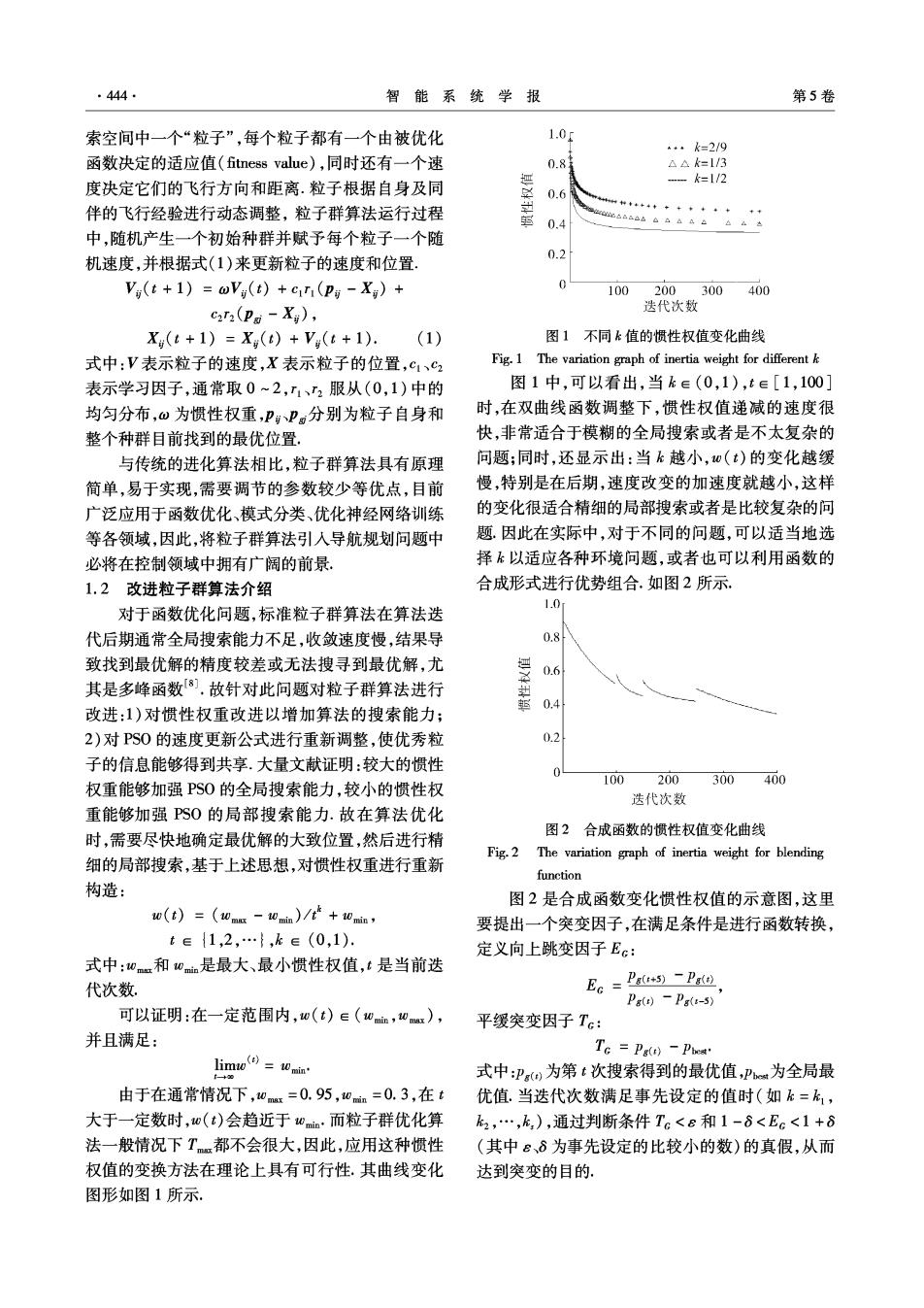
·444· 智能系统学报 第5卷 索空间中一个“粒子”,每个粒子都有一个由被优化 1.0r *··k=2/9 函数决定的适应值(fitness value),同时还有一个速 0.8 △△k=1/3 度决定它们的飞行方向和距离.粒子根据自身及同 -k=1/2 0.6 伴的飞行经验进行动态调整,粒子群算法运行过程 0.4 中,随机产生一个初始种群并赋予每个粒子一个随 机速度,并根据式(1)来更新粒子的速度和位置. 0.2 Vi(t+1)=@Vi(t)+cir(pi-X;)+ 100200300400 car2(pi-Xi), 迭代次数 X(t+1)=Xg(t)+V(t+1). (1) 图1不同k值的惯性权值变化曲线 式中:V表示粒子的速度,X表示粒子的位置,c1、c2 Fig.1 The variation graph of inertia weight for different k 表示学习因子,通常取0~2,11、2服从(0,1)中的 图1中,可以看出,当k∈(0,1),t∈[1,100] 均匀分布,o为惯性权重,PPg分别为粒子自身和 时,在双曲线函数调整下,惯性权值递减的速度很 整个种群目前找到的最优位置. 快,非常适合于模糊的全局搜索或者是不太复杂的 与传统的进化算法相比,粒子群算法具有原理 问题;同时,还显示出:当k越小,(t)的变化越缓 简单,易于实现,需要调节的参数较少等优点,目前 慢,特别是在后期,速度改变的加速度就越小,这样 广泛应用于函数优化、模式分类、优化神经网络训练 的变化很适合精细的局部搜索或者是比较复杂的问 等各领域,因此,将粒子群算法引入导航规划问题中 题.因此在实际中,对于不同的问题,可以适当地选 必将在控制领域中拥有广阔的前景。 择k以适应各种环境问题,或者也可以利用函数的 1.2改进粒子群算法介绍 合成形式进行优势组合.如图2所示 对于函数优化问题,标准粒子群算法在算法迭 1.0 代后期通常全局搜索能力不足,收敛速度慢,结果导 0.8 致找到最优解的精度较差或无法搜寻到最优解,尤 迴 0.6 其是多峰函数8],故针对此问题对粒子群算法进行 改进:1)对惯性权重改进以增加算法的搜索能力; 0.4 2)对PS0的速度更新公式进行重新调整,使优秀粒 0.2 子的信息能够得到共享.大量文献证明:较大的惯性 100 200 300400 权重能够加强PS0的全局搜索能力,较小的惯性权 迭代次数 重能够加强PS0的局部搜索能力.故在算法优化 图2合成函数的惯性权值变化曲线 时,需要尽快地确定最优解的大致位置,然后进行精 Fig.2 The variation graph of inertia weight for blending 细的局部搜索,基于上述思想,对惯性权重进行重新 function 构造: 图2是合成函数变化惯性权值的示意图,这里 w(t)=(wmat -wmin)/t+min, 要提出一个突变因子,在满足条件是进行函数转换, t∈{1,2,…},k∈(0,1). 定义向上跳变因子Ec: 式中:0mm和0m是最大、最小惯性权值,t是当前迭 代次数 Ee=Pa*-卫ge Pg(t)-Pa(t-s) 可以证明:在一定范围内,o(t)∈(win,0ax), 平缓突变因子Tc: 并且满足: Tc Pg(t)-Pwea 式中:Po为第t次搜索得到的最优值,P为全局最 由于在通常情况下,0x=0.95,0mn=0.3,在t 优值.当迭代次数满足事先设定的值时(如k=k, 大于一定数时,w(t)会趋近于wm·而粒子群优化算 k2,…,k,),通过判断条件Tc<e和1-6<Ee<1+6 法一般情况下Tm都不会很大,因此,应用这种惯性 (其中ε、6为事先设定的比较小的数)的真假,从而 权值的变换方法在理论上具有可行性.其曲线变化 达到突变的目的. 图形如图1所示
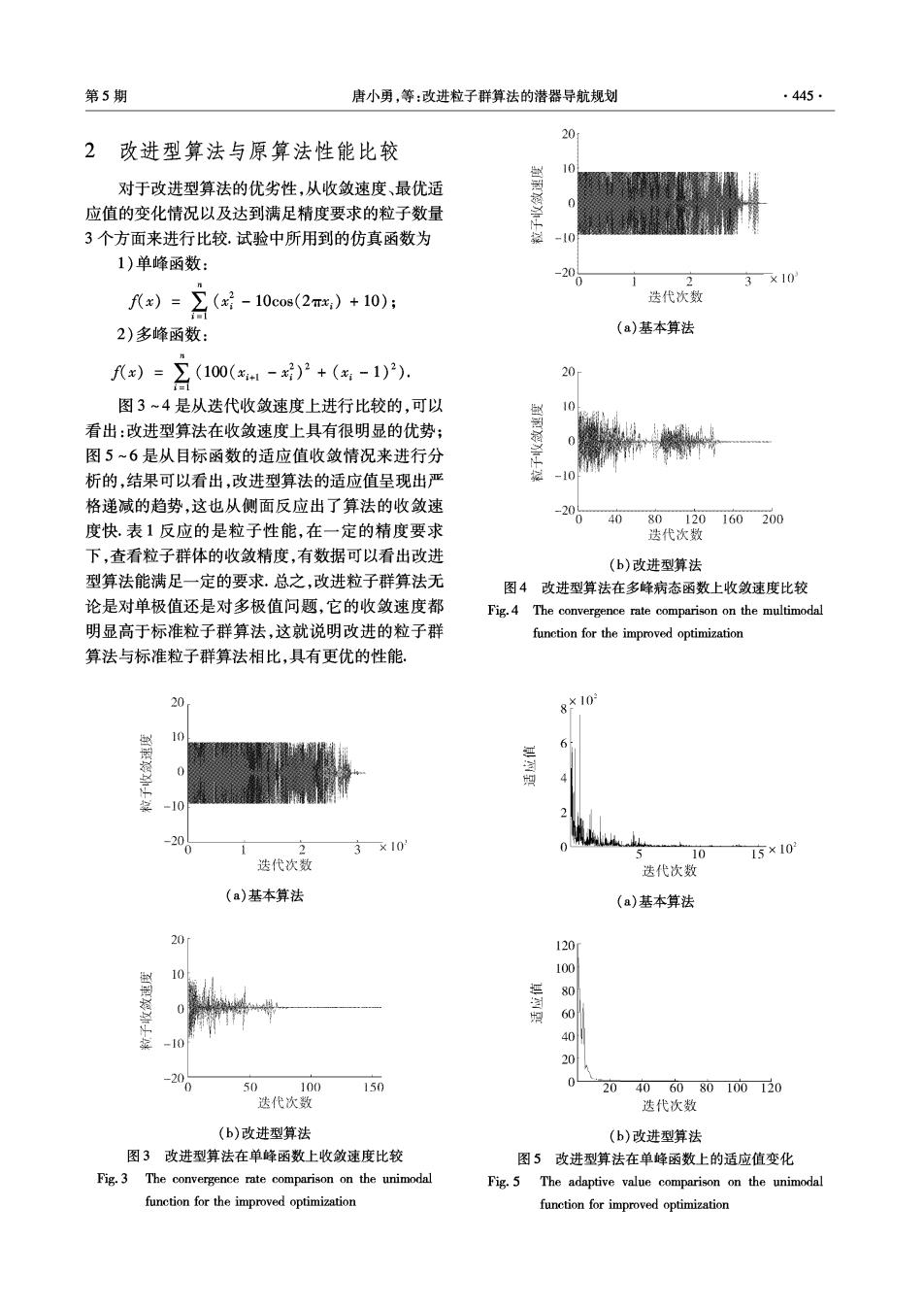
第5期 唐小勇,等:改进粒子群算法的潜器导航规划 ·445 20 2改进型算法与原算法性能比较 10 对于改进型算法的优劣性,从收敛速度、最优适 0 应值的变化情况以及达到满足精度要求的粒子数量 3个方面来进行比较.试验中所用到的仿真函数为 -10 1)单峰函数: 20 0 3×10 f)=∑(号-10cos(2mx,)+10); 迭代次致 2)多峰函数: (a)基本算法 到=召(10(-》+(气-10). 20 图3~4是从迭代收敛速度上进行比较的,可以 10 看出:改进型算法在收敛速度上具有很明显的优势; 图5~6是从目标函数的适应值收敛情况来进行分 析的,结果可以看出,改进型算法的适应值呈现出严 -10 格递减的趋势,这也从侧面反应出了算法的收敛速 -20 40 80120160200 度快.表1反应的是粒子性能,在一定的精度要求 迭代次数 下,查看粒子群体的收敛精度,有数据可以看出改进 (b)改进型算法 型算法能满足一定的要求.总之,改进粒子群算法无 图4改进型算法在多峰病态函数上收敛速度比较 论是对单极值还是对多极值问题,它的收敛速度都 Fig.4 The convergence rate comparison on the multimodal 明显高于标准粒子群算法,这就说明改进的粒子群 function for the improved optimization 算法与标准粒子群算法相比,具有更优的性能, 20 8*10 -10 -20 0 3×10 5 10 15×10 迭代次数 送代次数 (a)基本算法 (a)基本算法 20 120 100 0 50 -10 200 50 100 150 0 20 40 6080100120 迭代次数 迭代次数 (b)改进型算法 (b)改进型算法 图3改进型算法在单峰函数上收敛速度比较 图5改进型算法在单峰函数上的适应值变化 Fig.3 The convergence rate comparison on the unimodal Fig.5 The adaptive value comparison on the unimodal function for the improved optimization function for improved optimization

·446. 智能系统学报 第5卷 3)将潜器视为质点,障碍物的尺寸作适当拓展. 16 42 设S为起始点,G为目标点,每个障碍物在XY平面 10 内的圆心、半径已知.若以每个障碍物圆心的横坐标 8 6 为定值,纵坐标为变量,则可产生如图7中平行于纵 轴的虚线.潜器从起始点S到目标点G的无碰路径 2 12 16*10 即为寻找一个可行点的集合:P={S,P,P2,…,Pm, 迭代次数 G,其中P必须满足:1)P:为非障碍点;2)P与 (a)基本算法 相邻点的连线必须为可行路径,即2点之间的连线 不存在障碍.障碍物建立模型如下: 30 设起始点S和目标点G的坐标分别为(X,Y) 25 和(Xw,Yw),可行点P=(X,Y),则得到函数: 延 15 10 D=DaDrha Drs Drra 式中:Dr,表示点P和点P+之间的距离,以坐标 表示: 20 406080100120 迭代次数 D=> √(X41-X)2+(Y1-Y). (b)改进型算法 那么,导航规划的最终目标就转化为对该路径 图6改进型算法在多峰函数上的适应值变化 Fig.6 The adaptive value comparison on the multimodal 函数进行优化求解,即在Y(i=1,2,…,m)的取值 function for improved optimization 空间中寻找一组数值,使得路径最短,其中点P:和 点P:+1为非障碍点,且其连线不能存在障碍物, 表1实例数据分析 Table 1 Data analysis for example 单峰函数 多峰病态函数 次数 基本算法改进型算法 基本算法改进型算法 100 2 25 3 27 300 30 15 30 1000 20 30 18 30 3000 28 30 27 30 图7障碍物环境建模示意图 6000 30 30 30 30 Fig.7 Modeling of the space 全部达到4120 112 4512 96 注:此表中的数据是指在精度0.01时,达到要求的粒子数目. 3.2避碰检测 3导航规划环境建模方法 避碰检测的目的是判断当前的粒子所代表的路 3.1环境建模 径是否为可行路径.由于规划出的路径是由分段子 为了实现导航规划算法,对障碍物的建模方法 路径组合而成的,且子路径可以用相邻顶点的直线 应当尽量使其简单、易处理,使其符合时效性的特 来表示o: 点.因此,不考虑海洋环境对潜器的影响.为了使其 L:ax +by +c =0. 接近水下潜器的工作环境,将障碍物用其外接圆代 式中:a=y:-y-1,b=-1-,c=·y-1-x-1 替:对一个N边形的障碍物,将其各顶点连线的最 y·那么,是否与障碍物相撞就可以依据障碍物的圆 大值作为外接圆的直径,最大连线的中点即为圆心 心到直线的距离d与障碍圆的半径r(k)之间的关 并且对潜器在空间中运动做如下假设:1)潜器在水 系来判断:若障碍物满足条件d>r(k),则此路径为 下同一深度平面内运动;2)环境空间中分布有限个 可行路径;若障碍物满足条件d≤r(k),则此路径为 已知的静态障碍物,且不考虑障碍物的高度信息; 非可行路径,即潜器与障碍物碰撞

第5期 唐小勇,等:改进粒子群算法的潜器导航规划 ·447 3.3导航规划算法的实现流程 收敛速度有了明显的提高, 1)算法参数设定. 表2改进的粒子群算法与标准粒子群算法性能比较 2)出于避障考虑,对障碍物进行适当拓展, Table 2 The performance comparison of the improved 3)随机初始化每维粒子的位置、速度(初始化不 PSO 仅要考虑边界约束,还要考虑避障),及每维粒子的个 平均 平均 起始点 终点 算法 体最优位置P:和所有粒子的全局最优位置P 最优解收敛速度 (0.0) (28,0) Bpso 28.6072 760 4)更新粒子的速度,并进行边界约束(若粒子 (0,0) (28,0) Mpso 28.6072 138 的速度超出[-V,Vm],则以其边界值代替,更新 (0,0) (26,-2) Bpso 28.1607 780 粒子的位置,约束条件与3)类似 (0,0) (26,-2) Mpso 28.1607 68 (0,0) (26,1) Bpso 28.4085 940 5)避碰检测.检测粒子每一维Xa是否落入障 (0,0) (26,1) Mpso 28.4085 280 碍物中,两相邻顶点的连线是否为可行路径.若不满 足条件,则令Xa(t+1)=Xa(t). 5 结束语 6)对每个粒子X,求其适应值,更新Pg和P 相比于基本粒子群算法,本文对粒子群算法的 7)若算法达到最大迭代次数或者满足精度要 改进,使得粒子群算法在保持自身优点的情况下,在 求,则结束,否则转4) 收敛速度以及种群多样性的增加方面得到了提高. 4仿真结果及分析 仿真实验结果获得了从起点到终点的无碰撞路径, 证实了该方法的有效性和可行性.本文仅就静态已 基于所提出的方法,在AMD2.4GHz双核、1GB 知环境下的导航规划进行了建模与仿真,对于动态 内存的PC机上用Matlab7.0进行仿真实验.潜器用 实时环境以及海底三维环境条件下的导航规划还有 一个质点来表示,障碍物按其尺寸大小进行相应扩 待进一步研究。 张.潜器工作区域为28×22的矩形区域.粒子群维 数为n=3,粒子数为30.惯性权重o如式(3)所示, 参考文献: 随着迭代次数从0.85非线性递减到0.3,迭代次数 [1]肖本贤,李善寿,王晓伟,等.基于PS0和人工势场的机 定为1000次,以从起点到终点的无碰撞路径长度最 器人路径规划[J].合肥工业大学学报,2007,30(6): 短为优化目标,仿真结果如图8所示.该方法建模容 718-722. 易,理论简单,可在不同的障碍物环境下得到不同的 XIAO Benxian,LI Shanshou,WANG Xiaowei,et al.Path 优化轨迹,在全局路径规划中有一定可行性.该方法 planning of mobile robots based on PSO and APF[J].Jour- 可有效地解决潜器路径规划及避障问题, nal of Hefei University of Techenology,2007,30(6): 718-722. [2]张帆,周庆敏.基于遗传算法的移动机器人路径规划仿 真[J].微计算机信息,2008,24(6):267-268,284. ZHANG Fan,ZHOU Qingmin.A method based genetic for path of a mobile robot [J].Microcomputer Information, 2008,24(6):267-268,284 1015202530 [3]SARIMVEISH H,ALEXANDRIDIS A,MAZARAKISS,et 图8仿真实验结果 al.A new algorithm for developing dynamic radial basis Fig.8 Simulation results function neural network models based on genetic algorithms 图8反映出改进算法实现了无碰撞距离最短的 [J].Computers and Chemical Engineering,2004,28(1/ 路径规划.从表2可以看出,经过改进的算法在最优 2):209-217. [4]宋勇,李贻斌,栗春,等.基于神经网络的移动机器人路 解方面与标准粒子群算法一致,这主要是由被优化 径规划方法[J].系统工程与电子技术,2008,30(2): 函数的极值决定的(对于多峰函数,改进的粒子群 316-319. 算法具有明显的优越性).最显著的优势是其平均 SONG Yong,LI Yibin,LI Chun,et al.Path planning

·448 智能系统学报 第5卷 methods of mobile robot based on neural network[J].Sys- [10]毛宇峰,庞永杰,李晔,等.速度矢量坐标系下水下机器 tems Engineering and Electronics,2008,30(2):316-319. 人动态避障方法[J].哈尔滨工程大学学报,2010,31 [5]张建英,刘瞰.基于人工势场法的移动机器人最优路径 (2):159-164. 规划[J].航空学报,2007,8(2):4548. MAO Yufeng,PANG Yongjie,LI Ye,et al.Using a ve- ZHANG Jianying,LIU Tun.Optimized path planning of locity vector coordinate method for dynamic obstacle avoid- mobile robot based on artificial potential field [J].Acta ance of autonomous underwater vehicles [J].Journal of Aeronautica et Astronautica Sinica,2007,8(2):45-48. Harbin Engineering University,2010,31(2):159-164. [6]孙波,陈卫东,席裕庚.基于粒子群优化算法的移动机器 作者简介: 人全局路径规划[J].控制与决策,2005(9):1052 唐小勇,男,1985年生,硕士研究 1055. 生,主要研究方向为群智能算法。 SUN Bo,CHEN Weidong,XI Yugeng.Particle swarm opti- mization based global path planning for mobile robots[J]. Control and Decision,2005(9):1052-1055. [7]KENNEDY J,EBERHART R.Particle swarm optimization [C]//IEEE International Conference on Neural Networks. San Diege0,USA,1995:1942-1948. 于飞,男,1974年生,教授、博士 [8]KENNEDY J,MENDES R.Neighborhood topologies in 生导师,主要研究方向为系统仿真与建 fully imformed and best of neighborhood particles swarm 模.目前承担国家自然科学基金项目2 [J].IEEE Transactions on Systems,Man,and Cybernet- 项,博士后基金项目1项,发表学术论 ics-Part C:Applications and Reviews,2006,36(4):515- 文10余篇。 519. [9]郭冰洁,徐玉如,李岳明.水下机器人S面控制器的改进 粒子群优化[J刀.哈尔滨工程大学学报,2008,29(12): 潘洪悦,男,1985年,硕士研究生, 1277-1281. 主要研究方向为粒子群优化算法. GUO Bingjie,XU Yuru,LI Yueming.S surface controller for underwater vehicles using particle swarm optimization [J].Journal of Harbin Engineering University,2008,29 (12):1277-1281. 《机器人技术与应用》介绍 《机器人技术与应用》是由国家863机器人技术主题专家组和北方科技信息研究所共同主办的一本综合信息类刊 物,是我国惟一一本介绍机器人信息,传播机器人知识的刊物.本刊为国际机器人联合会(FR)会员单位,创刊于1988 年,是中国学术期刊(光盘版)与《中国期刊网》全文收录期刊,在国内自动化领域享有很高的声誉。 《机器人技术与应用》主要报道工业自动化、智能化机械及零部件、数控机床、机器人技术领域所取得的新技术、新成 果、科技动态与信息.传播企业信息和市场行情,交流业内创新成果,推动行业技术进步.主要栏目有专家访谈、企业家访 谈、主题工作动态、产品介绍、机器人比赛及综述等,涵盖面广,集知识性与趣味性于一体,具有很强的技术性和可读性。 读者对象主要是从事自动化、工程机械、数控机床、机械等行业的广大管理人员、技术人员、销售人员以及院校师生和机 器人爱好者. 希望更多的企业和个人与我们一起发展中国的机器人行业,提升中国装备制造业的智能化、信息化水平,使机器人 技术能够在我们国家经济建设中发挥更大的作用,使中国由制造大国迈向制造强国。 国内统一刊号:CN11-3520/TP,邮发代号82675,双月刊,大16开本,48页.定价10.00元/本,全年定价60.00元. 通讯地址:北京2413信箱41分箱《机器人技术与应用》杂志社(100089) 电话/传真:(010)68961813 邮 箱:robot(@onet.com.cm 网 址:www.rta.og.cn