
第6卷第2期 智能系统学报 Vol.6 No.2 2011年4月 CAAI Transactions on Intelligent Systems Apr.2011 doi:10.3969/i.i8sn.1673-4785.2011.02.015 用于DNA编码的部分字 李珍,王淑栋,李二艳 (山东科技大学信息科学与工程学院,山东青岛266510) 摘要:寻找合理的DNA编码是DNA计算中一个基本的问题.因此要给出一种方法使得DNA序列不会产生不想要 的结构,尤其是假阳性是解决此问题的关键.传统方法是要求码字间的Hamming距离足够大.因此考虑用部分字的 方法来解决DNA编码问题,利用部分字的洞的定义及其性质得到了关于部分字的洞、Hamming距离和Watson-Cick Hamming距离的3个命题,通过部分字对DNA编码进行了优化,解决了DNA编码中的部分疑难问题. 关键词:DNA编码;部分字;洞;Hamming距离;Watson-Crick Hamming距离 中图分类号:TP18文献标识码:A文章编号:16734785(2011)02018504 Partial words for DNA encoding LI Zhen,WANG Shudong,LI Eryan College of Information Science and Engineering,Shandong University of Science and Technology,Qingdao 266510,China) Abstract:Finding a good DNA code is a very basic problem in DNA computation.A solution must be provided which ensures that the strands involved do not exhibit any undesired behavior,and especially that they should not form a false positive.The traditional solution requires the Hamming distance between the words to be big enough. The author proposed the idea of considering only partial words for the solution of the DNA encoding problem.To some degree they already include the Hamming distance in the definition of compatibility.Thus,they can be used to simultaneously guarantee a desired distance and other properties.In this paper,the definition of Hole and some properties of partial words were applied to achieve three propositions concerning Hole,Hamming distance,and Watson-Crick Hamming distance.The DNA code set was optimized by using the partial words.Thus some difficult problems were resolved in DNA encoding. Keywords:DNA encoding;partial words;hole;Hamming distance;Watson-Crick Hamming distance 自从Adleman首次利用分子生物技术解决了法来解决DNA编码问题具有重要的意义.本文利用 一个具有7个顶点的有向Hamilton路问题以来,部分字的洞的定义及其性质得到了关于部分字的 DNA计算取得了突飞猛进的发展2s].DNA编码作洞、Hamming距离和Watson-Crick Hamming距离的 为DNA计算的基本问题之一也取得了很大的进3个命题,通过对部分字的分析对DNA编码进行了 展[sa].针对DNA编码中出现的错误杂交,Berstel 优化.随着部分字越来越受到人们的关注,它们可能 和Boasson'1于1998年提出了部分字的概念.2002 为DNA编码提供一种更为有效的工具 年,Blanchet-Sadris)对部分字的性质做出了详细论 证.2003年,Blanchet-Sadri67]又对部分字的性质 1基本定义及性质 作了更深入的研究与探讨.部分字的一些性质「8]包 定义14)字母表Σ={A,T,C,G上的部分字 含了DNA编码的一些限制条件,例如,部分字的相 w是由部分函数f:{0,1,…,n-1}→Σ随机排列构 容性包含了Hamming距离,因此考虑用部分字的方 成的DNA序列.w(p)(=f(),i∈{0,1,…,n-1}) 收稿日期:20100524. (p∈{0,1,…,n-1})有定义的位置构成的集合称 基金项目:国家自然科学基金资助项目(60503002):中国博士后科学 基金资助项目(20060400344). 为w的定义域,记为D(0),H(0)={0,1,…, 通信作者:李珍.E-mail:topwayD202@163.com n-1}/D(0)称为0的洞集合

·186 智能系统学报 第6卷 部分字主要是针对DNA序列的错误匹配提出 D(u)={0,2,3,4,5,7},D()={01,3,5,7}于是 的(见图1).,把此位置的碱基看成是未知的,即没 D(uVv)=D(u)UD(v)={0,1,2,3,4,5,7}, 有定义的位置,据定义1,这样的位置称为洞(而对 D(uA)=D(u)nD()={0,3,5,7},从而uVv= 于对应位置碱基相同的情况则不予考虑).因此,可 ATTCAToC,uAv=AooCoToC. 以将任意2条等长的DNA序列中相同位置碱基既 由以上定义可以得到如下命题, 不相同也不互补的位置称为洞. 命题1任意两相容的部分字,其最大字的洞 与Watson-Crick Hamming距离是一一对应的,即它 们最大字的洞的个数与Watson-Crick Hamming距离 T C GG T T A C A T T G T C A G 相等 图1发生2处错误匹配的DNA双链 证明设任意两相容的部分字为“、,包含于 Fig.1 DNA sequences with two mistakes u、v的最大字为w,由定义6可得D(0)=D(u)∩ 发生错误匹配的位置一般不能确定是哪个碱基 D(),从而H(w)=D(w)=D(u)∩D(v)=H(u)U 发生了错误匹配 H(v),故1H(w)|=IH(u)I+IH(v)I-IH(u)∩ 定义21设x=x2xy=yy2…y.∈{A,T,C H(v)l,又'(u,v)=IH(u)|+IH(v)I-IH(u)∩ <G}*,xy的Watson-Crick Hamming距离定义为 H()I,故二者相等,结论成立. (,)=, 2 DNA杂交反应与DNA编码优化 「1,x≠y,:≠y 实验结果研究表明14],2条DNA序列是否杂 式中xy:)= ,i=1,2,…,n,y是指 10,其他 交,不是取决于错误匹配的绝对数目,而是取决于错 在Watson-Cick碱基互补原则下与y:配对的碱基 误匹配的频率(错误匹配所占的比率),为此,引入 定义3[9]设Σ={A,T,C,G,0={A,T}, 穿洞率的定义. ={C,G则显然有o∩1=⑦.U1=.o、 定义8部分字w的穿洞率定义为r()= 定义为2个不同的类,则x和y中对应位置属于 Hole(o,其中Hole(o)表示w中洞的个数. 不同类的分量个数称为Watson-Crick Hamming距 穿洞率的大小与任意2个部分字的杂交情况有 离,记为H'(x,y). 定义4字母表U{o上的完全字。称为部 着密切的联系.研究表明,当(0)≥2时,任意2个 分字w的伴随,如果 部分字即使相应位置剩余所有碱基互补,则它们也 i]=[li],iD(w): 不能杂交.于是得到如下命题. 0, i华D(w)且0≤i≤|wl. 命题2任意两DNA序列xy,Ix|=IyI=n, 为简便起见,用部分字的伴随来代替部分字.例 如,用“部分oAoT字”来代替“部分字的伴随oAoT”. 当H(x,)≥2时,x与y不会发生杂交反应, 定义54任意2个等长的部分字u、v, 证明当(x)≥分且r()≥时,有 D(u)CD(v)且由ieD(u)可得u(i)=v(i),则称u 包含于v,记作uCu. 1(x)l≥2,1Hy)川≥2,1H(x)nH(y)1≤2.由 定义64]任意2个等长的部分字山、v,若存 命题1,H'(x,y)=IH(xAy)1=|H(x)I+ 在部分字0使uCw且vCW,则称u、v是相容的,记 作u↑. 1)1-1)n)1≥受+受-受=受,有以 由定义3~5得到如下定义. 上论述知命题成立 定义7任意2个相容部分字u、v、uVv表示包 含u、v的最小的字,即D(uV)=D(w)UD();uA 当r(o)<2时,任意两等长DNA序列错误匹 v表示包含于u、D的最大的字,即D(u八v)= 配情况如图2所示。 D(u)∩D(w). 例1设u=AoTCAToC,v=AToCoToC,则
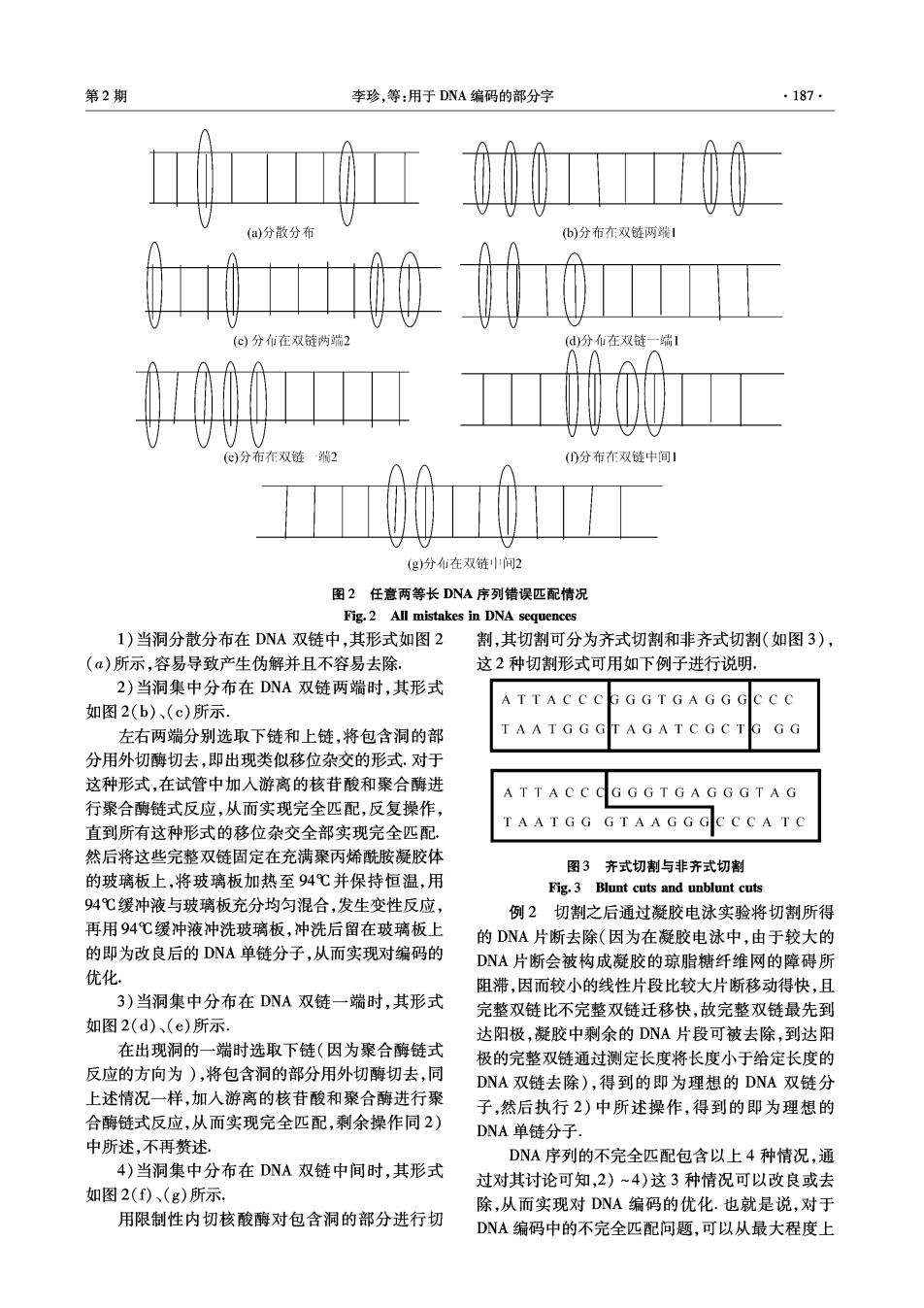
第2期 李珍,等:用于DNA编码的部分字 ·187· (a)分散分布 (b)分布在双链两端1 (c)分布在双链内端2 (d)分在双链一端】 ()分布在双链端2 ()分布布双链中间1 (g)分在双链中问2 图2任意两等长DNA序列错误匹配情况 Fig.2 All mistakes in DNA sequences 1)当洞分散分布在DNA双链中,其形式如图2 割,其切割可分为齐式切割和非齐式切割(如图3), (α)所示,容易导致产生伪解并且不容易去除. 这2种切割形式可用如下例子进行说明。 2)当洞集中分布在DNA双链两端时,其形式 ATTACCC GGTGAGGGCCC 如图2(b)、(c)所示 左右两端分别选取下链和上链,将包含洞的部 TAATGGG AGATCGCT G GG 分用外切酶切去,即出现类似移位杂交的形式.对于 这种形式,在试管中加入游离的核苷酸和聚合酶进 GGGTGAGGGTAG 行聚合酶链式反应,从而实现完全匹配,反复操作, CCCATC 直到所有这种形式的移位杂交全部实现完全匹配 GTAAGGG 然后将这些完整双链固定在充满聚丙烯酰胺凝胶体 图3齐式切割与非齐式切割 的玻璃板上,将玻璃板加热至94℃并保持恒温,用 Fig.3 Blunt cuts and unblunt cuts 94℃缓冲液与玻璃板充分均匀混合,发生变性反应, 例2切割之后通过凝胶电泳实验将切割所得 再用94℃缓冲液冲洗玻璃板,冲洗后留在玻璃板上 的DNA片断去除(因为在凝胶电泳中,由于较大的 的即为改良后的DNA单链分子,从而实现对编码的 DNA片断会被构成凝胶的琼脂糖纤维网的障碍所 优化. 阻滞,因而较小的线性片段比较大片断移动得快,且 3)当洞集中分布在DNA双链一端时,其形式 完整双链比不完整双链迁移快,故完整双链最先到 如图2(d)、(e)所示. 达阳极,凝胶中剩余的DNA片段可被去除,到达阳 在出现洞的一端时选取下链(因为聚合酶链式 极的完整双链通过测定长度将长度小于给定长度的 反应的方向为),将包含洞的部分用外切酶切去,同 DNA双链去除),得到的即为理想的DNA双链分 上述情况一样,加入游离的核苷酸和聚合酶进行聚 子,然后执行2)中所述操作,得到的即为理想的 合酶链式反应,从而实现完全匹配,剩余操作同2) DNA单链分子. 中所述,不再赘述 DNA序列的不完全匹配包含以上4种情况,通 4)当洞集中分布在DNA双链中间时,其形式 过对其讨论可知,2)~4)这3种情况可以改良或去 如图2()、(g)所示. 除,从而实现对DNA编码的优化.也就是说,对于 用限制性内切核酸酶对包含洞的部分进行切 DNA编码中的不完全匹配问题,可以从最大程度上

·188 智能系统学报 第6卷 加以优化 Pennsylvania,America,1997:230-273. [9]FELDKAMP,STEVENTS S E,NINO L F.A DNA se- 3结束语 quence complier[C]//Proceedings of 6th DIMACS Work- 通过引入部分字及其洞的定义和性质,可以从 shop on DNA Based Computing.Leidon,The Netherlands, 2000:253. 最大程度上解决DNA编码中的不完全匹配问题.众 [10]FRUTOS A G,BONEH D,DUNWORTH C.Demonstra- 所周知,DNA计算最主要和核心的反应为DNA分 tion of a word design strategy for DNA computing on sur- 子间的杂交反应,其效率和精度直接影响到DNA计 face[J].Nucleic Acids Research,1997,25(23):4748- 算的结果.DNA计算过程中的错误杂交分为假阳性 4757 和假阴性.假阴性的产生主要是由反应条件及生化 [11]ARITA M,JOHNSON C,ROTHEMUND P W I.The pow- 操作本身引起的,可通过控制生化反应条件来避免, er of sequence design in DNA computing[C]//The 4th In- 假阳性主要包括不完全匹配、移位杂交、双链形成的 terational Conference on Computational Intelligence and 发卡结构等.研究表明,合理的编码可以最大限度地 Multimedia Applications.[S.1.]2001:163-167. [12]BRAICH R S,JOHNSON C,ROTHEMUND P W K, 避免假阳性的出现.因此,DNA编码中不完全匹配 ADLEMAN L M.Solution of a satisfy problem on a gel- 问题的解决可以在一定程度上避免假阳性的出现, based DNA computer[C]//The 6th International Work- 为DNA编码理论的研究注入了活力.21世纪是生 shop on DNA Based Computing.London,UK:Springer- 物科学的世纪,且随着晶体管的宽度逐渐接近极限, verlag,2001:2742. DNA计算更成为人们普遍关注的一种计算模式. [13]DAN C,TULPAN HH,CONDON H.Anne.Condon. DNA编码是DNA计算的基本问题之一,这方面的 Stochastic local search algorithms for DNA word design 突破将有助于人们加深对DNA计算机的理解,促进 [C]//The 8th International Conference on Computational DNA计算机解决目前电子计算机所无法解决或者 Intelligence and Multimedia Applications.[S.1.]2003: 229-241. 很难解决的问题, [14]BERSTEL J,BOASSON L.Partial words and a theorem of 参考文献: fine and Wilf[J].Theoretical Computer Science,1999, 218:135-141. [1]ADLEMAN A L.Molecular computation of solution to com- [15]BLANCHET-SADRI F.HEGSTROM A.Partial words and binatorial problems[J].Science,1994,266 (11):1021- a theorem of fine and Wilf[J].Theoretical Computer Sci- 1024. ence,2002,270:401419. [2]LIPTON R J.NA solution of hard computational problems [16]BLANCHET-SADRI F.Primitive partial words C]//The [J].Science,1995,268:542-545. 8th International Conference on Computational Intelligence 3]BONEH D,DUNWORTH C,LIPTON R.Breaking DES u- and Multimedia Applications,[S.1.],2003,218:135- sing a molecular computer[C]//Proceedings of the 1st DI- 141. MACS Workshop on DNA Based Computers.Providence: [17]LEUPOLD P.Partial words for DNA coding[C]//The 8th American Mathematics Society,1995:37-65. International Conference on Computational Intelligence and [4]GARZON M,DEATON R,NEATHERY P.On the enco- Multimedia Applications.[S.1.]2005,221:224-234. ding problem for DNA computing[C]//Proceedings of the [19]王淑栋,宋弢.DNA Golay码的设计与分析[J].电子学 3rd DIMACS Workshop on DNA Based Computers.[S. 报,2009,37(7):135-141. 1.],1997:230-237. WANG Shudong,SONG Tao.The design and analysis of [5]OUYANG Qi,KAPLAN P D,LIU Shumao.DNA solution DNA Golay codes[J].Acta Electronica Sinica,2009,37 of the maximal clique problem [J].Science,1997,278: (7):135-141. 446-449. [20]陈鲁生,沈世镒.编码理论基础[M].北京:高等教育 [6]BAUM E B.DNA sequences useful for computation [C]// 出版社,2005:168-221. Proc Second Annual Meeting DNA-Based Computers.S. 作者简介: 1.],1996:223-227. 李珍,女,硕土.主要研究方向为 [7]GARZON M,DEATON R,NINO L F.A new metric for DNA计算. DNA computing[C]//Proceedings of the 2nd Annual Ge- netic Programming Conference GP-97.Morgan Kaufmann, USA,1997:472-487. [8]GARZOR M,DEATON R,NINO L F,STEVENS S E. WITTER M.Genome encoding for DNA computing[C]// The Third DIMACS Workshop on DNA Based Computing