
第5卷第4期 智能系统学报 Vol.5 No.4 2010年8月 CAAI Transactions on Intelligent Systems Aug.2010 doi:10.3969/i.i8sn.1673-4785.2010.04.009 均匀粒子群算法 刘宏达,马忠丽 (哈尔滨工程大学自动化学院,黑龙江哈尔滨150001) 摘要:由于粒子群算法本质上的随机性,其搜索质量和速度也呈随机性.这使得普通的粒子群算法难以满足某些 需要快速优化的工程需要.利用均匀设计方法产生S0算法的初始种群(或关键代次种群),可以使种群中的粒子在 搜索空间分布更均匀,更好地保持分散性.算法中给出了4种种群的生成方案,通过测试和对比分析表明:基于值域 分割的均匀设计种群生成法能使算法的搜索效果最好;算法可以在不丧失搜素精度和效率的前提下,提高搜素效率 和搜索精度的稳定性,有效减少粒子聚集和早熟的发生。 关键词:粒子群;均匀设计;实时优化;关键代次种群 中图分类号:文献标识码:A文章编号:16734785(2010)04033606 A particle swarm optimization algorithm based on uniform desig LIU Hong-da,MA Zhong-li College of Automation,Harbin Engineering University,Harbin 150001,China) Abstract:In a normal PSO algorithm,particle populations are usually produced randomly,leading to variations in search quality and speed.Such algorithms cannot be used to solve engineering problems that must be optimized quickly.In order to solve such problems,a PSO algorithm based on uniform design was used to generate initial PSO populations.This made the distribution of particles more uniform in the search space.Four methods for generation of particle swarms were studied.Test results showed that search precision was considerably improved if the genera- tion of a particle swarm by the uniform design method was based on value range division.That method maintained search efficiency and precision,stabilized search efficiency and precision,and reduced the possibility of swarm ag- gregation and premature convergence. Keywords:PSO;uniform design;real-time optimization;key population 目前优化算法的研究主要集中在搜索算法上,群优化算法.PS0算法的简洁性和快速性使它一 搜索算法分为确定性搜索法和随机性搜索法2种. 经提出便引起世界上许多研究者的极大关注, 在确定性搜索算法寻优过程中,一个搜索点到另一 由于粒子群算法种群产生的随机性,算法的搜 个搜索点的转移有确定的方法和规则,计算受初始 索质量和速度也呈随机性,一次测量不能反映粒子 点的影响较大,典型代表是禁忌搜索.随机性搜索算 群算法的性能,所以一般都是通过多次测量以均值 法在算法中加入随机性因素,并以一定概率接受比 和标准差的形式给出.但是,在某些需要实时优化的 当前解更差的解,所以计算不受初始点限制且提高 工程中,工作条件不允许进行多次优化.对这类问 了全局寻优性能,典型代表是模拟退火、免疫算法、 题,能否在算法搜索质量不会降低的情况下,能显著 蚁群算法和粒子群算法等. 提高算法解的稳定性和集中性,是研究的出发点, Kennedy和Eberhart(1995)受鸟群和鱼群运动 搜索算法初始种群的确定问题其实是一个如何 启发,并借用人类的决策过程中所采用的个体学习 利用有限个体来全面科学地表征所求问题解空间特 与文化传递的观念,将其用于优化问题,提出了粒子 征的优化设计问题.算法初始种群的确定间题实质 上是一个如何利用有限的个体来全面科学地表征问 收稿日期:20090905. 通信作者:刘宏达.E-mail:imhd405@163.com 题解空间特征的优化设计问题2.显然,对于初始

第4期 刘宏达,等:均匀粒子群算法 ·337· 种群既不能粗略地随机产生,也不能遍历所有的状 全局收敛性首先要解决的问题] 况,尤其是解决多变量问题时,只有将解空间中最有 当然,初始种群中若最优解的信息较少也可以 代表性的个体作为初始种群,才能更好地反映解空 通过群体的进化来得到,从而达到最优解,但由于 间的内在特征,从而较好地表征解空间23].文献 PS0算子本身的随机性,目前仅靠PS0算子是不能 [3]利用数论中的佳点集的理论和方法,对GA算法 确保算法搜索到最优解区域的.保持多样性的确可 中的交叉操作进行了重新设计,并应用于求解优化 以对算法的全局收敛性能进行改善,但这一多样性 问题、SAT问题、TSP问题和背包问题.通过模拟比 必须是具有一定代表性并将群体引导到有利于全局 较表明新的算法提高了计算的速度和精度,而且避 收敛的多样性 免了其他方法常有的早期收敛的现象.文献[4]在 另外,无论是从PS0算法的基础理论还是从算 层次色谱研究中,利用均与设计选择实验,再利用遗 子的运算方式上讲,粒子从自身和社会得来的经验 传算法探寻函数曲线,试验收到良好的效果.文献 对初始种群的依赖性都较强,而算法的搜索本身就 [5]利用正交设计的方法产生初始化种群;用正交 是靠粒子的位置运动实现的,所以,初始种群的优劣 交叉算子代替传统的算术交叉算子;利用Agent间 会对算法的快速性产生较大的影响.在无法预知最 的竞争作用与每个Aget所具有的知识和自学习能 优解所在区域的情况下,只有科学充分地代表解空 力进行启发式搜索.仿真试验和性能分析表明,算法 间特征的初始种群才能使算法以较优的方式快速逼 不但具有很强的全局优化能力和较快的收敛速度, 近最优解.可见,初始种群必须充分代表解空间的个 而且具有很强的鲁棒性.文献[6]将遗传算法的参 体,在有限数量内最大限度地表征所有个体的信息, 数设定描述为一个多因素多水平优化设计问题,同 达到初始种群在收敛性与快速性的协调统一.但初 时考虑到参数设定方法的可行性,提出应用解决多 始种群的合理性是较难判别的,尤其是多变量优化 问题就更加困难.随机产生的初始种群无法确保种 因素多水平优化设计问题的均匀设计方法设定遗传 群的合理性,当然也就无法确定算法的高效性.实际 算法的操作参数,实例应用仿真结果验证了这种方 上,确定初始种群的核心就是希望初始种群拥有合 法的可行性、有效性.通过比较,其中均匀设计法性 理的多样性并在尽可能少的代数内将寻优搜索引导 价比最高,但也存在着当因素的个数和等级增多时, 到最优解区域 对应的均匀设计表很难得到,所产生的初始种群的 如上所述,粒子群算法初始种群的确定问题其 多样性保持不好的不足, 实是一个如何利用有限个体来全面科学地表征所求 该文将均匀试验设计和粒子群算法相结合,提 问题解空间特征的优化设计问题.显然,对于初始种 出了均匀粒子群算法(PS0 based on uniform desig, 群既不能粗略随机产生,也不能遍历空间中所有点 UD-PS0).该算法不但充分考虑粒子的记忆特性,而 的情况,只有将解空间中最有代表性的个体作为初 且考虑粒子群中粒子分布的均匀性,使粒子能更好 始种群,才能更好地反映解空间的内在特征,从而较 地适应周围环境,从而引导粒子群不断进化,最终达 好地表征解空间.在试验范围内均匀散布的特点,使 到全局优化的目的.为了当因素的个数和等级增多 均匀设计成为解决这个问题的有益思路 时均匀设计法的不足,引入了4种种群生成方案,测 试效果表明,可以很好地解决了此问题 2标准粒子群算法和均匀设计 1算法提出背景 2.1标准粒子群算法 目前标准粒子群算法被公认的有2种,这里使 由于传统PS0的初始种群是随机选取的,初 用LDW-PSO.它是这样规定的:粒子群运动在一个 始种群的覆盖空间具有很大的不确定性,如果初始 n维搜索空间中,种群(x,…,xm)由m个粒子组成. 种群空间不包含全局最优解的信息,而算法算子又 x:=(1,x2…,xn)为第i个粒子的位置,每个粒子 不能在有限的进化代数内将覆盖空间扩延到全局最 的速度为:=(1,v2,…,n).其个体极值为P:,种 优解所在的区域,那么过早收敛就不可避免.到目前 群的最优值为Pg,粒子x:按式(1)和(2)更新自己 为止,还无法证明在有限迭代次数内,PS0算法一定 每一维的速度和位置: 能达到全局最优解所在的区域.所以,确保初始种群 t城=oma+CI1(pia-xia)+c2,(pd-xa), 的多样性与个体分布的相对合理性就成了改善PS0 (1)

·338 智能系统学报 第5卷 x站=a+t. (2) 种均匀设计方案;而方案的选择不同,试验的效果也 式中:d=1,2,…,n,i=1,2,…,m.m是种群规模,t 大不一样.评价各设计方案好坏一般用均匀性度量 是当前进化代数,1、c2为加速因子.惯性权值采用 指标来实现。均匀度越小表示方案的均匀性越好,通 Shi建议的线性递减权值(liner degression weight,. 常利用偏差(discrepancy)最小为标准,从均匀设计 LDW)策略来控制惯性权重,即 表中选出均匀性最好的。列,这一过程也被称为使 w=Wini-(wini -wend)t/Tms (3) 用表的选择。均匀性度量常用的准则有:偏差准则 式中:Tn为最大进化代数;Wa为初始惯性权值;wd D、L2偏差、修正的L2偏差MD2、中心化L2偏差 为进化至最大代数时的惯性权值,并推荐取值为 CD2、对称L2-偏差SD2、可卷L2偏差WD2、散度准 0m=0.9,0ed=0.4. 则、海明距等).中心化L2偏差CD,取消了原点的 2.2均匀设计简介和均匀设计表的构建 特殊地位,对数据比较灵敏,测试结果比较合理,现 2.2.1均匀设计简介 在使用的许多均匀设计表都是采用它来设计的.下 均匀设计78]是由我国数学家方开泰和王元于 面给出对于均匀设计Un(g),中心化L2偏差的计 1981年提出的.它是基于数论中的一致分布理论,将 算公式 数论和多元统计相结合,从均匀性角度出发,基于试 验点在整个试验范围内均匀散布的一种试验设计方 cn.P)=(-元a2+- 法.对于n个因素q个水平的试验,它从q”个试验组 合中选出g个在解空间分布均匀的组合进行试验,与 -的+8+引 正交设计至少需要g次试验相比较,试验次数大大 减少,在许多多水平试验的问题中非常实用.与正交 w-°-3y- (4) 设计相比,均匀设计为试验者提供更多的选择,可以 3 算法的实现 用较少的试验获得期望的结果,这使得均匀设计特别 适合于多因素.多水平的试验和系统模型完全未知的 将粒子群算法的问题域划分为适当多的水平, 情况.它已成为统计试验设计的重要方法之一 在这些水平中均匀地取值,就可以使生成的粒子均 2.2.2均匀设计表的构建 匀分布在问题域中.设w:是均匀设计表U(n)中的 要进行均匀试验设计,首先需要选择均匀设计 元素,令ag=(2-1)/2n,j=1,2,…,n,则集合 表,均匀设计表(简称均匀表)是均匀设计的基础。 Pm={ak=(a1,a2,…,aa),k=1,2,…,m是[0, 每一个均匀设计表都有一个代号,等水平的均匀设 1]”中的均匀分布的m个点.图1表示的是在2维 计表可用U.(q),其中U表示均匀设计,n为均匀 空间中,利用均匀设计的方法和随机方法产生的点 表的行数(也就是需要做的试验数),9为每个因素 集分布情况. 的水平数,s为均匀表的列数.当水平数q为偶数 从图1可以看出,均匀设计的方法产生的点集所 时,U(q)的均匀性较差,所以方开泰等人建议用 构成的初始群体比随机的初始群体更能从统计意义上 U(g)代替.通常,同因素、同水平的均匀表 反映出目标函数的特性.随机分布的初始群体在分布 U(q)比U(q)有更好的均匀性,应优先选用.如 的分散性上,不如均匀设计的方法产生的点集 果各个因素的水平数目不同,则选用均匀表U,( 1.0 1.0 ×9驼,…×明),其中,s(1≤≤)表示具有不同水平 0.8 0.8 的因素数目,4,(1≤i≤)表示与s相应的水平数目。 40.6 0.6 。。 ●。 0.4 0.4 均匀设计表的构造方法有很多,如好格子点法 0.2 0.2 。 (good loattice point,GLP)、拉丁方法(latin hyper- 04 0.20.40.60.81.0 0 0.20.40.60.81.0 11 cube,LH)、正交表扩充法(expending orthogonal de- (a)均匀法产生的初始点 (b)随机法产生的初始点 sig卿,EOD)、优化搜索法以及RBIBO法等34.由于易 图1均匀法和随机法产生的初始点集 于编程实现,好格子法和方幂生成向量法被使用的最 Fig.1 Initial dots brought by uniform design and ran- 为普遍.当然也可以使用已算好的均匀设计表 dom method 对因素数为s和水平数为n的试验,可产生C

第4期 刘宏达,等:均匀粒子群算法 ·339· 3.1关键代次种群生成的基本步骤 当被优化问题需要的种群规模较大时,均匀设 算法实现的关键在于:根据问题选择合适的种 计的表中的水平也要增大,此时为了选择均匀使用 群粒子数n,并确定待优化问题维数D,按照表1的 表的计算量将很大.例如种群规模为60,需设计 对应关系,设计一个U.(n”)均匀设计表 U0(60),即使采用方幂生成向量法也需要比较几 表1均匀设计表和PS0算法种群的关系 十组可能列来选出生成向量.为了便于应用,降低计 Table 1 Relationship of uniform design table and parame- 算复杂性,希望应用目前现有的生成向量表.但由于 ters of PSO 目前常用的修正好格子点法生成向量表最多只有 均匀设计均匀设计表 PSO算法 31水平,即只能得到31个个体,这显然不能满足大 n 水平 行数 群中的粒子数 种群规模的要求, D因素 列数 待优化变量维数 那么,是否可以利用低水平均匀设计表近似代 以构建初始种群为例,给出关键代次种群生成 替30以上的高水平均匀设计表呢?通过分析和查 的基本步骤: 找资料,提出以下2种方案. 1)根据给定的n,生成等水平均匀表Un(nm), 3)是利用中心化偏差对坐标系旋转有不变 得到对应的均匀设计矩阵Un×m; 性2],将n/2水平的均匀设计表中的任2列交换 2)根据待优化问题的维数D,求得CD偏差最 便得到另一均匀性等价的n/2水平均匀设计表,利 小的矩阵U.xD,其中UnxD=(g),i∈I jelp 用它们共同组成n个个体的均匀表.当种群规模大 3)按照g=(2vg-1)/2n,将v转化为[0,1]中 于30时,如种群规模为40,则种群可由u20(203)的 的点山; 20个个体和其均匀性等价的u0(203)的20个个体 4)转换为X={xgI儿≤xg≤h}中的初始点: 共同构成.由于每一个体都是其所处水平上的均匀 设计个体即都具有均匀性.同时,这2组个体又是均 5)得出初始种群=+(,亿-),iel,jelm n. 匀性等价的,不存在各区域的相互作用组合问题,所 在具体应用时,可以利用提前算好的U.xD,例 以,较大限度地在简化计算的同时,尽可能地保特了 如利用文献[13]可以直接获得推荐的CD2偏差最 种群的均匀性, 小的矩阵U.x0·这样直接可以进入基本步骤的4), 4)是将取值区域l,≤x≤h分割成s份,在每份 所以算法复杂度并未增加多少. 中采用一个均匀表.例如,如种群规模为40,则种群 3.2不同种群规模的种群生成方法 可由U0(20)的20个个体分别在分割区域1和分 文献[13]只提供了中心化L2偏差最小的均匀使 割区域2产生一个U0x5的矩阵 用表的最大因素数29.也就是说,如直接利用文献[13] 4实验的设置与测试 进行均匀粒子群设计,粒子数最大只能选到29, 3.2.1小种群规模的算法实现 4.1测试环境和对象 一般情况下,粒子群算法的粒子数取20~ 对F:Sphere函数,F2:Schaffer's函数,F3: 309),这里将其称为小种群规模.这时可以通过均 Ackley函数,F4:Griewank函数,Fs:Rastrigin函数, 匀设计表直接产生初始种群(或关键代次种群).由 F6:Rosenbrock函数分别就进行了测试,变量域统 于一般问题只需取粒子数为30即可,所以只要利用 取为,问题维数统一取30(Schaffer为2维). 等水平均匀表U(30°)设计即可.但是目前直接可 在对方案1和2的测试中,测试分别基于LDW- 以使用的均匀表最多只能进行30个因素的试验,而 PS0和GLDW-PS021进行.以此对比均匀设计法和 具有中心化L2偏差最小的均匀使用表的最大因素 随机法产生初始种群时,算法表现出来的搜索性能 数29,所以尝试用2种方案来解决.1)随机生成一 PS0种群规模为m=30,学习因子c1=c2=2,惯性 个粒子补充进入.2)利用均匀等价准则0](均匀设 权重w随在迭代过程中线性递减,变化范围是 计方案阵的任2列交换所得新方案与原方案在均匀 0.9~0.4,T=0.5.均匀设计表选择U0(309). 性相同意义下是等价的),将均匀阵UxD任意一些 在对方案3和4的测试中,基本表(均匀设计表 列互调位置,然后随机抽取一列,作为第30列: 和使用表)使用方案1所用的表.测试都是基于 3.2.2大种群规模的算法实现 LDW-PS0进行,其中学习因子c,=c2=2,惯性权重
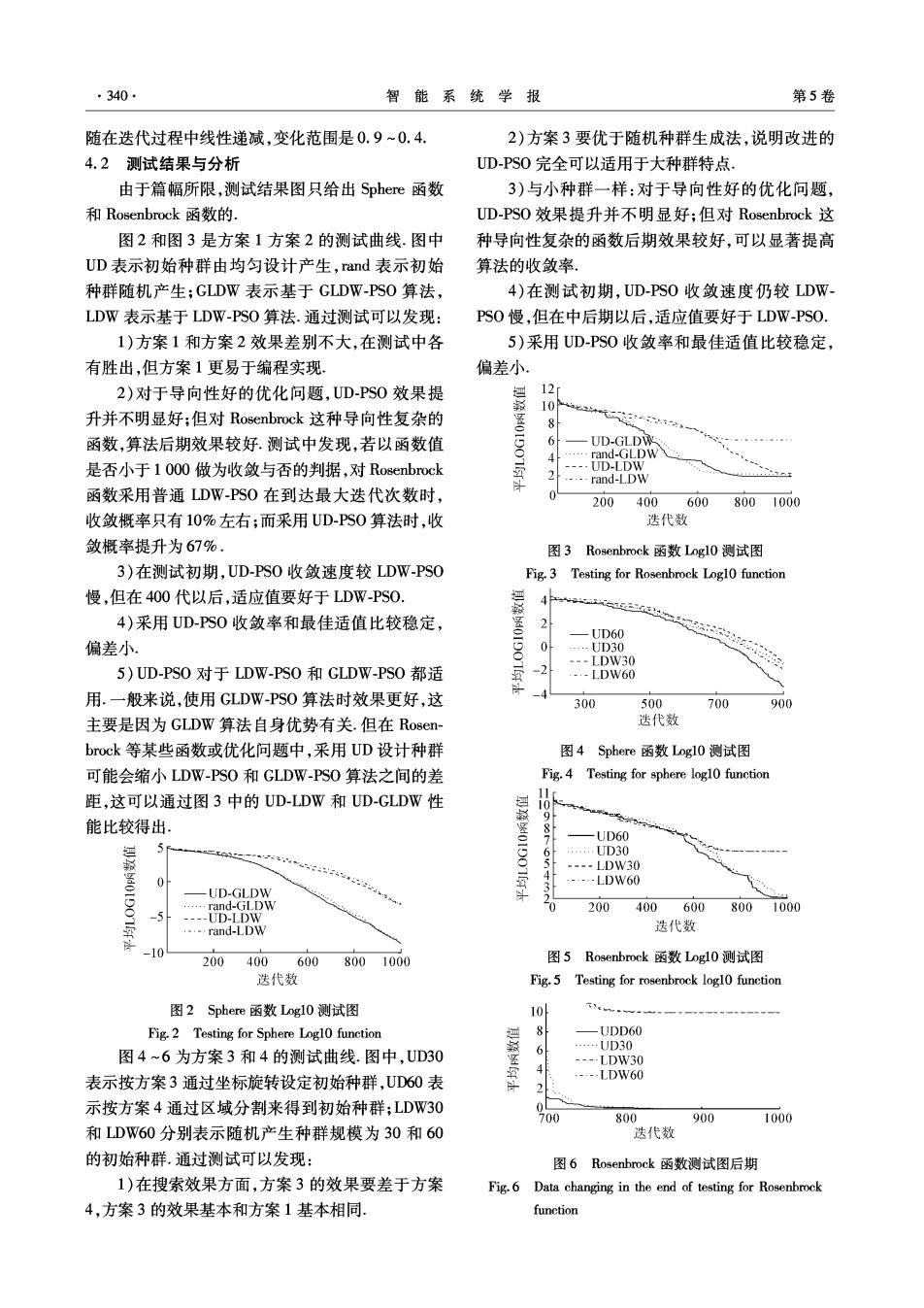
340 智能系统学报 第5卷 随在迭代过程中线性递减,变化范围是0.9~0.4. 2)方案3要优于随机种群生成法,说明改进的 4.2测试结果与分析 UD-PS0完全可以适用于大种群特点, 由于篇幅所限,测试结果图只给出Sphere函数 3)与小种群一样:对于导向性好的优化问题, 和Rosenbrock函数的, UD-PS0效果提升并不明显好;但对Rosenbrock这 图2和图3是方案1方案2的测试曲线.图中 种导向性复杂的函数后期效果较好,可以显著提高 UD表示初始种群由均匀设计产生,rand表示初始 算法的收敛率。 种群随机产生;GLDW表示基于GLDW-PSO算法, 4)在测试初期,UD-PS0收敛速度仍较LDW- LDW表示基于LDW-PSO算法.通过测试可以发现: PS0慢,但在中后期以后,适应值要好于LDW-PS0. 1)方案1和方案2效果差别不大,在测试中各 5)采用UD-PS0收敛率和最佳适值比较稳定, 有胜出,但方案1更易于编程实现 偏差小 2)对于导向性好的优化问题,UD-PS0效果提 12 10 升并不明显好;但对Rosenbrock这种导向性复杂的 8 函数,算法后期效果较好.测试中发现,若以函数值 UD-GLDW 是否小于1000做为收敛与否的判据,对Rosenbrock 挪Pw 2 ---rand-LDW 函数采用普通LDW-PS0在到达最大迭代次数时, 0 200 4006008001000 收敛概率只有10%左右;而采用UD-PS0算法时,收 迭代数 敛概率提升为67%. 图3 Rosenbrock函数Logl0测试图 3)在测试初期,UD-PS0收敛速度较LDW-PSO Fig.3 Testing for Rosenbrock Logl0 function 慢,但在400代以后,适应值要好于LDW-PS0, 泗 4 4)采用UD-PS0收敛率和最佳适值比较稳定, 2 -UD60 偏差小 0 -UD30 -=-LDW30 5)UD-PS0对于LDW-PS0和GLDW-PS0都适 -2 -.-LDW60 用.一般来说,使用GLDW-PS0算法时效果更好,这 300 500 700 900 主要是因为GLDW算法自身优势有关.但在Rosen- 迭代数 brock等某些函数或优化问题中,采用UD设计种群 图4 Sphere函数Logl0测试图 可能会缩小LDW-PSO和GLDW-PS0算法之间的差 Fig.4 Testing for sphere logl0 function 距,这可以通过图3中的UD-LDW和UD-GLDW性 11 能比较得出. -UD60 妇 …UD30 ---.LDW30 0 4 ---LDW60 -UD-GLDW .....rand-GLDW 0 200 400600 8001000 ----UD-IDW …rand-LDW 迭代数 2004006008001000 图5 Rosenbrock函数Logl0测试图 迭代数 Fig.5 Testing for rosenbrock log10 function 图2 Sphere函数Logl0测试图 101 . Fig.2 Testing for Sphere Logl0 function 8 -UDD60 …UD30 图4~6为方案3和4的测试曲线.图中,UD30 6 ---LDW30 表示按方案3通过坐标旋转设定初始种群,UD60表 .-.-LDW60 2 示按方案4通过区域分割来得到初始种群;LDW30 00 700 800 900 1000 和LDW60分别表示随机产生种群规模为30和60 迭代数 的初始种群.通过测试可以发现: 图6 Rosenbrock函数测试图后期 1)在搜索效果方面,方案3的效果要差于方案 Fig.6 Data changing in the end of testing for Rosenbrock 4,方案3的效果基本和方案1基本相同 function

第4期 刘宏达,等:均匀粒子群算法 341 HE Dakuo,WANG Fuli,ZHANG Chunmei.Establishment 5 结束语 of parameters of genetic algorithm based on uniform design 针对粒子群算法搜索效率随机,普通的粒子群 [J].Joural of Northeastem University:Natural Science, 算法难以满足某些实时优化的工程需要的现状,提 2003,24(05):409411. [7]方开泰,马长兴.正交与均匀试验设计[M].北京:科学 出了基于均匀设计法确定关键代次种群的S0算 出版社,2001:89-105. 法.利用均匀设计方法产生PS0算法的初始种群, [8]QIN Hong,ZHANG Shangli,FANG Kaitai.Constructing u- 使种群中的粒子在搜索空间分布更好地保持均匀分 niform designs with two-or three-level.Acta Mathematica 散性.提出和对比了4种均匀设计方案,且都没有增 Scientia,2006,26(3):451459. 加算法计算复杂性.通过测试和对比分析表明,新算 [9]ZHENG Yongling,MA Longhua,ZHANG liyan,QIAN Jix- 法能明显影响粒子的收敛性、快速性,能使算法具有 in.On the convergence analysis and parameter selection in 更稳定的搜索效率和搜索精度,减少粒子聚集和搜 particle swarm optimization[C]//Proceedings of the and In- 索早熟的发生 ternational Conference on Machine Learning and Cybernet- ics.Xi'an,China,2003:1802-1807. 参考文献: [10]孙先仿,范跃祖,宁文如.U均匀设计的均匀性研究 [1]KENNEDY J E R.Particle swarm optimization[C]//Proc [J].应用概率统计,2001,17(4):341-345, of IEEE Interational Conference on Neural Networks. SUN Xianfang,FAN Yaozu,NING Wenru.On the uni- Perth,WA,USA,1995:1942-1948. formity of U'uniform designs[J].Chinese Journal of ap- [2]刘宏达.粒子群算法的研究及其在船舶工程中的应用 plied probability and statistics,2001,17(4):341-345. [D].哈尔滨:哈尔滨工程大学,2007 [11]HICKERNELL F J.A generalized discrepancy and quadra- LIU Hongda.Research of particle swarm optimization algo- ture error bound J].Math Computation,1998,67:299 322. rithm andilts application in ship engineering[D].Harbin: Harbin Engineering University,2007. [12 ]FANG K T,QIN H.A note on construction of nearly uni- [3]张铃,张钹.佳点集遗传算法[J].计算机学报,2001,24 form De-signs with large number of runs[J].Statistics and (09):917-922. Probability Letters,2003,61(2):215-224. ZHANG Ling,ZHANG Bo.Good point set based genetic [13]Fang Kaitai.http://www.math.hkbu.edu.hk/Uniform algorithm[J].Chinese Journal of Computers,2001,24 Design/. (9):917-922. 作者简介: [4]XUE Guochen,XIN Li.Application of uniform design and 刘宏达,男,1976年生,副教授,主 genetic algorithm in optimization of reversed-phase chroma- 要研究方向为群智能理论及其应用,在 tographic separation[J].Chemometrics and Intelligent La- 群智能领域发表论文12篇. boratory Systems,2003,68(2):157-166. [5]薛明志,钟伟才,刘静,焦李成.正交Multi--Agent遗传算 法及其性能分析[J].控制与决策,2004,19(3):290- 294. XUE Mingzhi,ZHONG Weicai,LIU Jing,JIAO Licheng 马忠丽,女,1974年生,副教授,主 Orthogonal multi-Agent genetic algorithm and its perform- 要研究方向为机器视觉检测技术, ance analysis[J].Control and Decision,2004,19(3):290- 294 [6]何大阔,王福利,张春梅.基于均匀设计的遗传算法参数 设定[J].东北大学学报:自然科学版,2003,24(05): 409-411