
第5卷第4期 智能系统学报 Vol.5 No.4 2010年8月 CAAI Transactions on Intelligent Systems Aug.2010 doi:10.3969/j.is9n.1673-4785.2010.04.005 平均邻近间隔支撑向量机 王晓明,王士同 (江南大学信息工程学院,江苏无锡214122) 摘要:近年来,支撑向量机(SVMs)作为一种学习方法已经在机器学习和模式识别的研究领域中得到了成功的运 用,然而传统SVMs缺少考虑数据的局部信息.文中将邻近间隔的基本思想引入到SVMs中,提出了平均邻近间隔支 撑向量机(ANMSVMs).ANMSVMs继承了传统SVMs的优点,同时又充分利用了数据的局部信息,从而实现了泛化能 力的进一步提高。人造数据和真实数据集的实验结果验证了该方法有效性,并且相对于传统SVM:体现出了更强的 泛化能力. 关键词:监督学习;支撑向量机:邻近间隔 中图分类号:TP181文献标识码:A文章编号:16734785(2010)040313-07 Using average neighborhood margin with support vector WANF Xiao-ming,WANG Shi-tong (School of Information,Jiangnan University,Wuxi 214122,China) Abstract:The support vector machine (SVM)is a learning method used successfully in the fields of machine learn- ing and pattern recognition.However,traditional SVMs have not taken local information,or the environment of the data,into full consideration.To provide this context,an average neighborhood margin support vector machine (ANMSVM)was formulated by introducing the basic theories of neighborhood margins into SVMs.This method in- herits the characteristics of traditional SVMs,yet also fully considers the local information surrounding the data, and thus shows better learning performance.Experimental results on artificial and real datasets indicated the effec- tiveness of an ANMSVM. Keywords:supervised learning;support vector machine;neighborhood margin 近年来,支撑向量机(support vector machines,样本到超平面的间隔距离最大化来实现的,仅仅考 SVMs)1-]已经在机器学习和模式识别领域的研究 虑了每类数据边界上的样本点,而缺少考虑样本数 中引起了广泛的关注,成为了广大学者的研究热点 据的局部信息,从而在一定程度上制约了其泛化能 之一.由于SVMs具有结构简单、泛化能力(General- 力的进一步提高.但是在一些特征排序和特征提取 ization)强等优点,并且有着坚实的统计学习理论基 的算法中,数据的局部信息得到了充分的利用.这些 础,能处理线性和非线性的情况,目标优化问题可以 算法的共同点就是通过采用邻近间隔(neighborhood 通过偶形式化为一个较易处理的优化问题,所以在 mar罗in)的基本思想来充分利用数据的局部特征.在 众多的研究和应用(如人脸识别)、图像检索4、语 这些算法中,邻近间隔的基本思想主要体现在对每 音识别等)都中引起了广泛的关注,并取得了显 一个样本点都首先建立2个邻域集合:一个是由样 著的成果 本点的同类数据中的飞个最邻近样本组成的集合, 然而,传统的SVMs建立决策超平面是通过使 另一个则是由样本点的异类数据中的K个最邻近 收稿日期:200909-13. 样本组成的集合.然后再利用所有样本点的这2个 基金项目:国家自然科学基金资助项目(60704047):国家“863”计划 资助项目(2007AA1Z158、2006AA10Z313). 邻域集合来构建特征排序或特征提取的目标函数: 通信作者:王士同.E-mail:wxwangst(@yahoo..com.cm. 在这些方法中,典型的是RELIEF6、I-RELIEF(Ier

·314· 智能系统学报 第5卷 ative RELIEF)I7 SNMMC stepwise nonparametric 面的向量: margin maximum criterion)(s ANMM average z:=|x:-NM(x,)|-|x:-NH(x:)I.(2) neighborhood margin maximization)[9]算法.这些算法 式中:WH(x:)表示样本点x同类中最近的样本点, 充分利用了数据的局部性和整体性,简单而且有效 NM(x:)表示异类中最近的样本点.然后I-RELIEF 在本文中,为了克服传统的SVMs缺少考虑数据 算法定义如下的优化问题: 局部信息的缺点,把邻近间隔的基本思想引入到SVMs (3) 中,提出了平均邻近间隔支撑向量机(average neighbor- maxw∑z,8.t.ww=1,w≥0. hood margin support vector machines,ANMSVMs). I-RELIEF算法采用了迭代的方法来求解上面优化 法显著的特征是即保留传统SVMs的优点,同时又充分 问题中的w,最后也根据w来排序特征的重要性.在 考虑了数据的局部特征,而且还可以转化为标准的 文献[10]中,作者把I-RELIEF推广到了特征提取 SVMs优化问题,从而能够利用SVMs现有的各种软件 方法中。 来解决ANMSVMs问题.首先利用每一个训练样本点的 1.2基于邻近间隔的特征提取算法 2个邻域定义了平均邻近间隔向量,然后利用所有样本 在特征提取方法中,SNMMC8]算法也采用了邻 点的平均邻近间隔向量建立了ANMSVMs的优化问题. 近间隔的基本思想.当提取一维特征时,SNMMC算 从距离定义的方式讲,ANMSVMs采用了马氏距离,而 法定义了下面的优化目标函数: SVMs则直接采用了欧式距离.文中分析该方法和 SVMs的联系,也讨论其非线性化的问题.实验结果验 muw(名a(1芯I2-I8I)m, 证该方法的有效性,并且相对于传统的SVMs,其表现 8.t.ww=1. (4) 出了更强的泛化能力. 式中:w:表示的是样本权重,6=x:-x表示样本 点x:与其异类样本集中最近样本点的差值向量, 1基于邻近间隔的特征排序和特征提取 6=x:-x则表示样本点x:与其同类样本集中最近 样本点的差值向量,‖·‖表示向量的L2范数.值 文中假定有一个由N个样本组成的数据集X= 得注意的是,在SNMMC算法中采用了差值向量的 [:…xw],Hx:∈R“,X∈RMxw,所有样本分属于2 L2范数,而在RELIEF算法中则采用了差值向量的 个不同的类别,用X,表示第L(L=1,2)类数据子 绝对值 集,其中共含有N个样本,y:表示样本x:的类别标 由于SNMMC算法易受例外样本点的影响,在 号,∈{1,-1} 文[9]中作者针对这个问题提出了ANMM算法.在 1.1基于邻近间隔的特征排序 ANMM算法中,首先定义了: REL正F6]算法是一种经典的特征排序算法.该 算法对每一维特征的鉴别能力进行估计时,首先找 %=5-Σ) 到每一个样本x的2个邻域集合:一个是样本点x 式中:W表示样本点x:异类的近邻样本组成的样本 同类(Ht)数据集中距离样本x最近的样本点 集,该样本集的样本数为W;表示样本点x:同类 NH(x),另一个是样本点x异类(Mss)样本集中距 的近邻样本组成的样本集,该样本集的样本数为 离样本x最近的样本点NM(x);然后对每一维特征 N.然后ANMM算法定义了下面的优化问题: 的权重采用了如下的方式进行更新: w:=w;+lxNM (x)Ix-NH (x)I.(1) maxw(∑Y)w,8.t.ww=1. (6) 式中:x表示样本x点的第i维特征,0:表示第i维 通过上面的介绍可以看出,这些算法共同的一 特征的权重,「·|表示求绝对值,最后利用0:来对 点就是利用了样本点的同类近邻样本和异类近邻样 特征进行排序。 本,依据这2个近邻集之间的差异来判断特征的鉴 I-RELIEF算法是RELIEF算法的改进版本, 别能力,充分考虑了数据的局部特征.不同的是在特 在I-RELIEF算法中,首先对于样本点x:定义了下 征排序中采用了差值向量的绝对值,在特征提取中

第4期 王晓明,等:平均邻近间隔支撑向量机 ·315· 则采用了差值向量的L2范数 决策超平面却不能反映数据的特点: 7 2线性平均邻近间隔支撑向量机 oclassl 6 o class2 5 svm- 2.1线性平均邻近间隔支撑向量机 0000 0000 ◇0◇Q o000 首先基于样本的邻近间隔思想,对于样本点x: 0060 0000 定义如下的向量: g89,0 0000 0000 () K -anmsvm (7) 10 15 式中:N(x:)表示样本点x:的同类样本集中K个 图1人造数据情况下ANMSVMs和SVMs所对应的决 最近样本点组成的样本集,W,则表示x:的异类样 策超平面 本集中K个最近样本点组成的样本集,K表示近邻 Fig.1 The decision superplanes constructed by ANMSVMs 数.注意,这里的向量z与前面RELIEF和ANMM and SVMson the artificial dataset 算法中的定义不同.它是同类邻域中的K个最近样 类似于SVMs,可以把(ANMSVMs)的优化问题 本点的平均差向量减去了异类邻域中的K个最近 (10)转化为其对偶优化问题来求解.利用拉格朗日 样本点的平均差向量,称其为样本点x:的平均邻近 法,假定矩阵Z是非奇异(对于Z奇异的情况, 间隔向量,利用所有样本点x:的平均邻近间隔向量 将在后面进行介绍),可以得的优化问题(10)的对 z:,定义线性可分平均邻近间隔支撑向量机(ANMS 偶优化问题为 VMs)的优化问题为 mgs-a Ha +'a. min∑w'zzw, 8t.∑a=0,0≤a4≤C,i=1,2,…,N(12) 8.t.wx:+b≥1,i=1,2,…,N, (8) 式中:Hg=yyxZ-,a°=[c1a2…aw]TeR".假 令 定式(12)的最优解为a'=[a1a2…aw]T,利用 Z=. (9) KKT条件1]可以得到原始优化问题(10)的的最 a 注意,矩阵Z是对称的,并且具有半正定性.为 优解为 了统一数据线性可分和不可分的情况,通过引入了 松弛变量专:(当:都为0时对应于线性可分的情 w-2y (13) 况),则上面的优化问题(8)可以改写为 对于i,0<a<C,类似于SVMs,称x:为支撑向 量.用Dsv来表示支撑向量集,Nsy表示支撑向量个 卿zw+c宫, 数.此时,根据KKT条件有y,([w]x:+b*)= 8.t.y(w'x+b)≥1-5,5:≥0,i=1,2,…,N 1,可以据此得到b的最优解.但是为了使计算更可 (10) 靠,通常取所有支撑向量的均值,即: 式中:C为惩罚参数.假定{w·,b°,专·}是上述优化 问题的最优解,则ANMSVMs建立的决策超平面为 6=五: (14) 把最优解{w·,b·}代入式(11),可以得到线性情况 [p”]x+b*=0,决策函数是: 下ANMSVMs的决策函数为 f(r)=8gn([w]'x+b*). (11) 图1给出了在一个人造数据情况下ANMSVM8 f)=8g(∑(xz-x)+b).(15) 和SVMs所对应的决策超平面.从中可以看出,由于 通过前面的讨论,可以得到线性ANMSVMs算法. ANMSVMs算法考虑了数据的局部信息,其得到的 算法1:线性ANMSVMs 决策面超平面充分反映数据的特点,然而SVMs的

.316. 智能系统学报 第5卷 1)利用式(7)和(9)建立矩阵Z: 2)求解出优化问题(12),得到其最优解为 0 a'=[&a…aw]T; 8.t.y:(px:+b)≥1,i=1,2,…,N.(19) 3)利用式(12)和(14)得到; 证明见附录 4)利用上一步得到的最优解{w·,b·}并根据 由于亚空间是S,非零特征值对应的特征向量 式(15)建立ANMSVMs的决策函数 张成的空间,假定S,非零特征值有m个,则业空间 2.2小样本的问题 就是m维,根据线性代数理论,其必然和m维的R 在前面都假定了矩阵Z(其是M×M矩阵)是 空间同构.所以存在标准正交的P∈RMxm使得v= 非奇异的,然而在实际应用中则可能出现奇异的情 P)成立,这里v∈亚,4∈R".一般情况下矩阵P可 况,尤其是在小样本数据中.在这种情况下可以采用 以用S,非零特征值所对应的特征向量组成,这样式 Z的伪逆2来代替其逆矩阵.为了计算矩阵Z的伪 (19)就转换为 逆,首先对矩阵进行奇异值分解 Z PAPT. mi270, (16) L,0 式中:M=diag(入1,入2,…,入m)包含了矩阵Z的大于 s.t.y(nx:+b)≥1,i=1,2,…,N(20) 0的特征值,m是矩阵Z的秩,P为矩阵Z的大于0 式中:7∈Rm,x=Px,根据引理1和式(20),可以 的特征值所对应的特征向量组成矩阵,从而,矩阵Z 认为在空间R“中应用SVMs等价于在与业空间同 的伪逆是 构的R空间中应用SVMs.因此,可以得到下面的 Z*=PA-PT. (17) 引理 引理2:非线性SVMs KPCA线性SVMs. 3 非线性平均邻近间隔支撑向量机 这里仅对引理2进行简单的分析.由于非线性 的SVMs是首先采用核函数把样本映射到特征空 由于矩阵Z是由每一个样本点x的平均邻近 间,然后再在这个特征空间中应用线性SVMs算法; 间隔向量z:构成,然而邻近间隔向量z:中却含有对 然而由引理1可知,在特征空间中应用SVMs等价 向量的元素求绝对值对于,因而ANMSVMs不能直 于在与业空间同构的欧氏空间中应用SVMs.这个 接非线性化.这里将首先对非线性SVMs进行分析, 过程中先采用核函数把样本映射到特征空间,然后 然后依据相同的原理引出了非线性的ANMSVMs.. 再采用P℃A算法把特征空间中的数据投影到与亚 首先来分析一下线性SVMs和PCAU13]相结合 空间同构的欧氏空间中,实际上相当于直接采用 的一个性质.在PCA算法中,定义总体散度矩阵: KPCA[5]算法对原始数据进行投影变换.所以,非线 5=含(x-m)(出-m),这里m太名,文献 性的SVMs等价与先采用KP℃A把原始数据投影到 [14]指出,对于S,的特征向量,用亚表示其非零特 一个新的数据空间,然后再在这个空间中应用线性 征值对应的特征向量张成的空间,Ⅱ表示零特征值 SVMs. 对应的特征向量所张成的空间,则空间亚和空间Ⅱ 所以,对于非线性的ANMSVMs,也可以采用相 是互补空间并一起组成了S,的特征向量空间.对于 同的方式,即首先采用KPCA把数据投影到一个新 SVMs,有以下定理: 的数据空间(称其为变换数据空间),然后再在这个 引理1:对于任意w∈R“,w都可以表示成w= 数据空间中应用线性ANMSVMs算法.因此对于非 v+Y,这里v∈业,y∈Ⅱ.从而定义的SVMs的优化 线性的ANMSVMs,可以在变换数据空间中建立如 问题 下的优化问题: N 1 i2”w, 8.t.y:(w'x:+b)≥1,i=1,2,…,N.(18) 8.t.y:(wx:+b)≥1-专,5:≥0,i=1,2,…,N 可以等价表示为 (21)

第4期 王晓明,等:平均邻近间隔支撑向量机 ·317· 式中:x:为在采用KPCA投影后的变换数据空间中 20 o classl o class2 样本点x:所对应的新样本,之为采用KPCA投影后 15 的投影数据空间中根据式(7)和(9)建立的矩阵.假 1.0 定优化问题(21)的最优解为{·,b”,专·},则可以 05 。 得到非线性的ANMSVMs的决策函数为 f(x)sgn([w*]+b*). (22) 0.5 d 这里,E表示未知类别信息的样本点x采用KPCA -l. 投影后在变换数据空间中所对应的新样本 2.0-15-1.00.50051.015202.53.0 由上,可以得到非线性ANMSVMs算法: (a)非线件SVMs 算法2:非线性ANMSVMs 20 o classl 1)利用KPCA把数据投影到一个新的数据空间 o class2 15 中,利用式(7)和(9)建立矩阵; 1.0 2)求解出优化问题(21),得到其最优解为; 05 0000 3)利用上一步得到的最优解并根据式(22)建 0 立非线性ANMSVMs的决策函数. ® 05 4实验结果及分析 -1. 20-15-1.00.5005101520253.0 1 为了验证本文提出的ANMSVM8算法的可行性 (b)非线性ANMSVMs 以及泛化能力,在这一部分内容中将进行实验研究, 图2two-moons数据中采用高斯核的情况下ANMSVMs 把它和传统的SVMs进行了比较.实验分为2部分. 和SVMs所对应的决策超平面 在第一部分实验中通过人工拟合数据来演示了AN Fig.2 The decision superplanes constructed by ANMSVMs MSVMs和SVMs在非线性情况下构造的决策超平 and SVMs in the rbf.kemel case on the two-moons 面的不同;在第2部分实验中,采用了10个UCI6 dataset 数据来测试和比较了ANMSVMs和SVMs在线性情 4.2UCI数据 况和非线性情况下的泛化能力.在实验中,对于 在这一部分的实验中采用了10个UCI的数据 SVMs采用了LIBSVM7] 来进一步测试ANMSVM8的泛化能力.表4给出这 4.1拟合数据 些数据的基本信息.其中的数据既有2类的情况,也 前面图1演示了ANMSVMs算法和SVMs算法 有多类的情况.对于多类的情况,采用了一对一的方 在线性情况下构造数据决策超平面时的不同.在这 式「18].在进行实验前,所有数据都把其每一维特征 一个实验中,将通过2个拟合数据进一步揭示在非 处理为均值为0,方差为1.实验中,采用了5重交叉 线性情况下它们之间的区别.图2采用的数据是two 测试(Cross alidation)I181精度作为泛化性能的度量 -moons数据集.这里采用了高斯核,核参数为5.图 标准.5重交叉测试就是把数据样本平均划分为5 2的(a)是直接采用了非线性SVMs结果,(b)给出 部分,进行5次训练测试过程,然后计算出这5次测 了非线性的ANMSVMs结果,也即是采用了KPCA+ 试的平均测试精度.在第1次训练测试过程中,把数 线性ANMSVMs的方法.从这些实验结果中可以看 据的第1部分作为测试数据集,剩下的数据集作为 出,文中提供的ANMSVMs非线性化方式是有效的, 训练数据集;第2次训练测试过程是把数据的第2 并且由于ANMSVMs算法进一步利用数据的局部信 部分数据作为测试数据集,其它的数据集作为训练 息,相对于SVMs,其构造出的决策超平面更加反映 数据集.依照这样的过程,直到所有5次训练测试过 了数据的特征 程做完.在本文中,就是把这5次训练测试的平均测 试精度作为泛化性能的评估准则
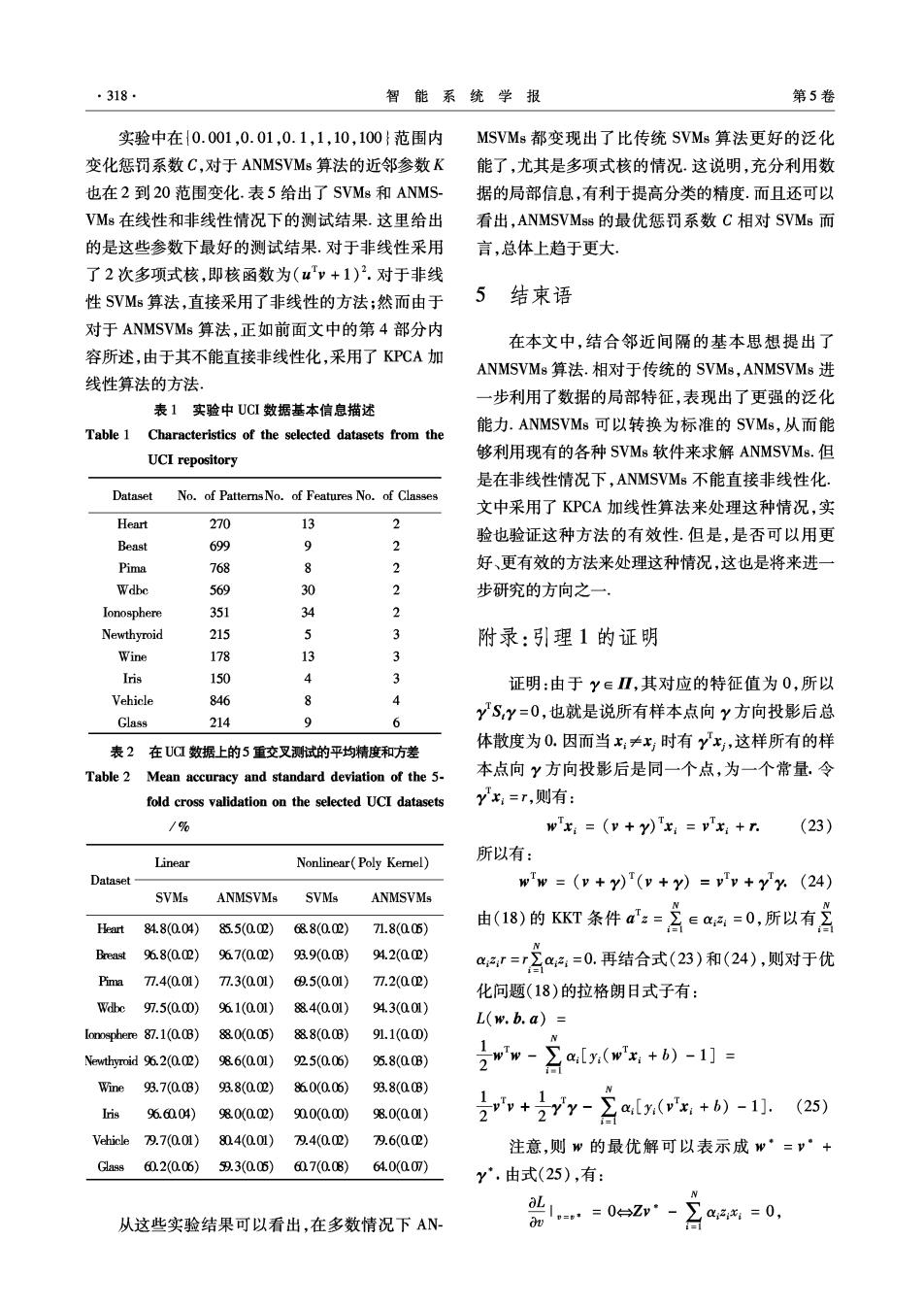
318, 智能系统学报 第5卷 实验中在{0.001,0.01,0.1,1,10,100}范围内 MSVMs都变现出了比传统SVMs算法更好的泛化 变化惩罚系数C,对于ANMSVMs算法的近邻参数K 能了,尤其是多项式核的情况.这说明,充分利用数 也在2到20范围变化.表5给出了SVMs和ANMS 据的局部信息,有利于提高分类的精度.而且还可以 VMs在线性和非线性情况下的测试结果.这里给出 看出,ANMSVMss的最优惩罚系数C相对SVMs而 的是这些参数下最好的测试结果.对于非线性采用 言,总体上趋于更大 了2次多项式核,即核函数为('v+1)2.对于非线 性SVMs算法,直接采用了非线性的方法;然而由于 5结束语 对于ANMSVMs算法,正如前面文中的第4部分内 在本文中,结合邻近间隔的基本思想提出了 容所述,由于其不能直接非线性化,采用了KPCA加 ANMSVMs算法.相对于传统的SVMs,ANMSVM8进 线性算法的方法, 一步利用了数据的局部特征,表现出了更强的泛化 表1实验中UCI数据基本信息描述 Table 1 能力.ANMSVMs可以转换为标准的SVMs,从而能 Characteristics of the selected datasets from the UCI repository 够利用现有的各种SVMs软件来求解ANMSVMs..但 是在非线性情况下,ANMSVMs不能直接非线性化. Dataset No.of PatternsNo.of Features No.of Classes 文中采用了KPCA加线性算法来处理这种情况,实 Heart 270 3 2 2 验也验证这种方法的有效性.但是,是否可以用更 Beast 699 9 Pima 768 8 2 好、更有效的方法来处理这种情况,这也是将来进一 Wdbe 569 30 2 步研究的方向之一 Ionosphere 351 34 2 Newthyroid 215 5 3 附录:引理1的证明 Wine 178 13 3 Iris 150 4 3 证明:由于Y∈Ⅱ,其对应的特征值为0,所以 Vehicle 846 8 4 YSY=0,也就是说所有样本点向Y方向投影后总 Glass 214 9 6 在UC数据上的5重交叉测试的平均精度和方差 体散度为0.因而当x:≠,时有yx,这样所有的样 表2 Table 2 Mean accuracy and standard deviation of the 5- 本点向Y方向投影后是同一个点,为一个常量.令 fold cross validation on the selected UCI datasets yx:=T,则有: /% wxi=(v +y)'x:=v'x:+r. (23) Linear Nonlinear(Poly Kemel) 所以有: Dataset w'w (+y)(v+y)=v'v+yy.(24) SVMs ANMSVMs SVMs ANMSVMs Heart 84.8(0.04) 85.5(0.02) 68.8(0.02) 71.8(005) 由(18)的KKT条件a=含ee=0,所以有名 Breast 96.8(0.02) 967(0.02) 93.9(0.0B) 94.2(002) r=r召:=0.再结合式(23)和(24),则对于优 Pima 77.4(0.01) 77.3(0.01) 69.5(0.01) 7.2(02) 化问题(18)的拉格朗日式子有: Wdbc 97.5(0.00) 961(0.01) 8840.01) 94.3(001) L(w.b.a)= lonosphere 87.1(0.0B) 880(0.05) 888(0.0B) 91.1(000) Newthyroid 96.2(0.02) 8.6(0.01) 925(0.06) 95.8(00B) 2w- ∑a,[y.(wx+b)-1]= Wine 93.7(0.0B) 9男.8(0.02) 860(0.06) 93.8(0B) Iris 966004) 980(0.02) 900(0.00) 98.0(001) +27y-含a(ix+b)-1.(25) Vehicle 79.7(0.01) 804(0.01) 9.4(0.02) 9.6(02) 注意,则w的最优解可以表示成w·=y·+ Ga9s60.2(0.06) 59.3(0.05)60.7(0.08) 64.0(007) y°.由式(25),有: 1,=02y- a=0, 从这些实验结果可以看出,在多数情况下AN

第4期 王晓明,等:平均邻近间隔支撑向量机 ·319· =09y=0. (26) [11]FLETCHER R.Practical methods of optimization [M]. y 2nd ed.New:York Wiley,1987:81-82 注意,式(26)与式(19)所提出的优化问题的拉 [12]LIU J,CHEN S C,TAN X Y.Efficient pseudo-inverse 格朗日式子是一样的,假定v*∈亚是它的最优解, linear discriminant analysis and its nonlinear form for face 又由于y·=0,则w的最优解可以表示成w·=v·. recognition[J].Intemational Journal of Patter Recognition 证毕。 and Artifcial Intelligence,2008. [13 LIPOVETSKY S.PCA and SVD with nonnegative load- 参考文献: ings.Pattern Recognition,2009,42(1):68-76. [14]杨键,杨静宇,叶晖,等.Fisher线性鉴别分析的理论 [1]VAPNIK V.Statistical learning theory M].New York: 研究及其应用[J].自动化学报,2003,29(4):482 Wley,1998:13-18 493. [2]SCHOLKOPF B,SMOLA A.Leaming with kemels M]. [15]WANG L,PANG Y W,SHEN D Y,et al.An iterative al- Cambridge,MA:MIT Press,2002:25-32. gorithm for robust kemel principal component analysis [3]ER M J,CHEN W,WU S.High-speed face recognition [C]//2007 International Conference on Machine Learning based on discrete cosine transform and RBF neural networks [J].IEEE Transanctions on Neural Networks,2005,16 and Cyberetics,.2007,(6):3484-3489, [16]ASUNCION A,NEWMAN D.J.UCI machine learning re- (3):679691. pository EB/OL].http://www.ics.uci.edu/~mlearn/ [4]TONG S,CHANG E.Support vector machine active learn- MLRepository.html,2007. ing for image retrieval[C]//Proceedings of ACM Interna- [17]CHANG CC,LIN C J.LIBSVM:a library for support tional Conference on Multimedia,2001:107-118. vector machines EB/OL].Software available at http:// [5]GANAPATHIRAJU A,HAMAKER JE,PICONE J.Appli- www.csie.ntu.edu.tw/~cjlin/libsvm 2001. cations of support vector machines to speech recognition [18]ABRIL L G,ANGULO C,VELASCO F,et al.A note on [J].IEEE Transactions on Signal Processing,2004,52 the bias in SVMs for multi-classification J].IEEE (8):2348-2355. Transanctions on Neural Networks,2008,19(4):723- [6]KIRA K,RENDELL L A.A practical approach to feature 725. selection[C]//Proc Ninth Int'1 Conf Machine Learning. 作者简介: [s.1.],1992:249-256. 王晓明,男,1977年生,博士研究 [7]SUN Y J.Iterative RELIEF for feature weighting:algo- 生,主要研究方向为机器学习,模式识 rithms,theories,and applications[J].IEEE Transactions 别,图像处理。 on Patter Analysis and Machine Intelligence,2007,29 (6):1035-1051 [8]QIU X,WU L.Face Recognition by stepwise nonparametric margin maximum criterion C]//Proc ICCV.2005:1567- 王士同,男,1964年生,教授,博导, 1572. 主要研究方向为模式识别,模糊系统, [9]WANG F,ZHANG C S.Feature extraction by maximizing 生物信息学,先后十多次留学英国、日 the average neighborhood margin[C]/Proe ICCV.Beijing, 本和香港地区,在国内外重要杂志上发 2007:1-8. 表学术论文数十篇, [10]SUN Y J,WU Dapeng:A RELIEF based feature extraction algorithm[C]/sDM.[s.1.],2008:188-195