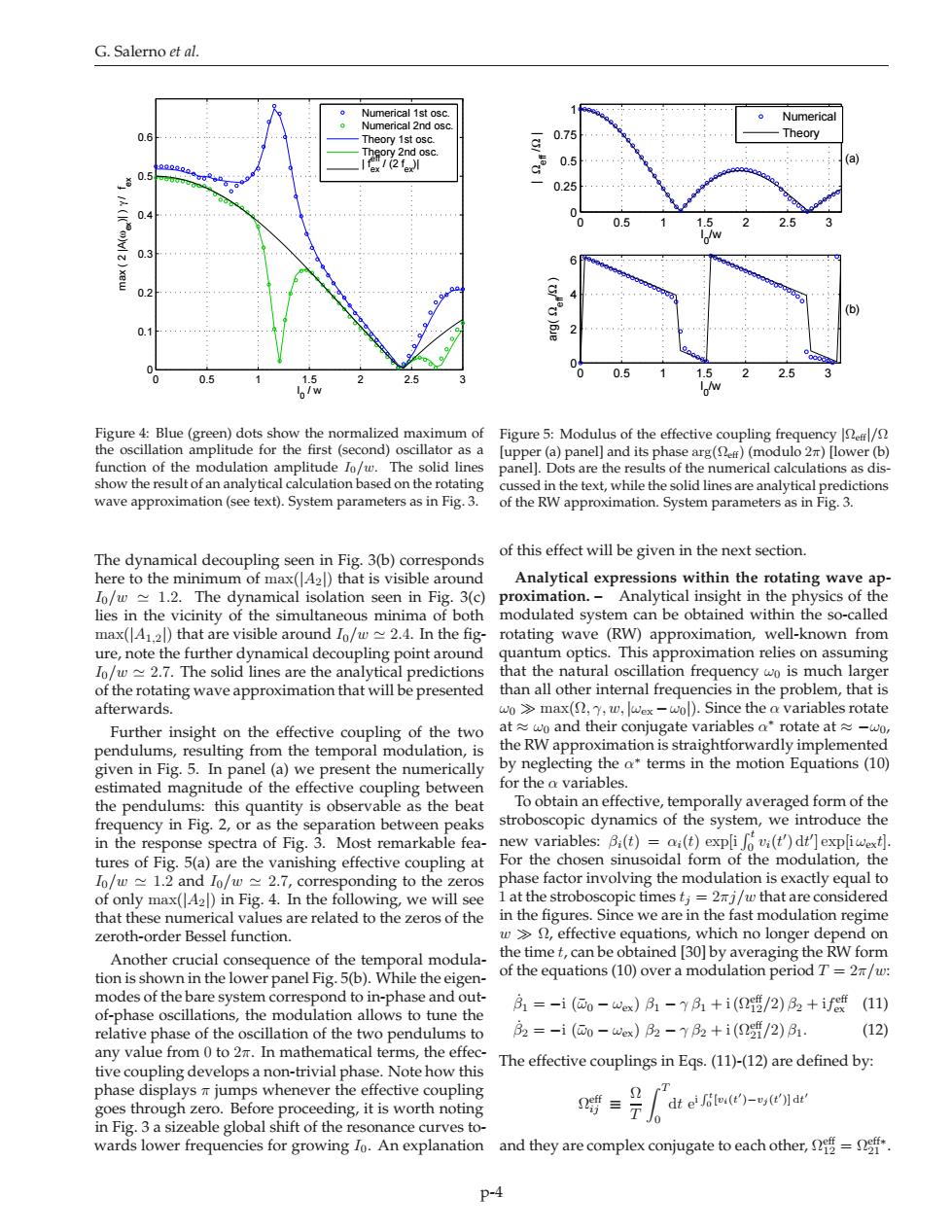
G.Salerno et al. 0.7 0.5 0.25 0.5 22.5 0.2 0。 05 6 25 0.5 225 Figure 5 e sold lines numerical calculations as dis wave approximation (see text).System parameters as in Fig3 of this effect will be given in the next section /w1.2.The dynamical isolation seen in Fig.3(c) modulated system can be obtained within the so-called max(A)that 2.4.In the fig rotating wave solid yamical (RW)approximation,well-known from e point aroun is much larg of the rotating wave approximation that will be presented than all other internal frequencies in the problem,that is afterwards. Further insight on the effective coupling of the two rdtaeat pendulums,resulting from the temporal modulation,is given in Fig.5.In panel (a)we present the num by neglecting the aterms in the motion Equations (10) for the a variables the pendulums:this quantity is observable as the beat espectra of eh福 ing efre to at )e phase factor involving the modulation is exactly equal to Iat the stroboscopic that are considered we are in th function no od tion er panel Fig.5 of the equations(10)over a modulation period T=2/w: of-phase oscillations,the modulation allows to tune the =-i(@0-)品1-+i2港/2)32+if(11) relative phase of the oscillation of the two 2=-i(-we)-1+i(/2) (12 any valu 2T. In math ical t the The effective couplings in Eqs.(11)-(12)are defined by nlin and they are complex conjugate to each other,= p-4G. Salerno et al. 0 0.5 1 1.5 2 2.5 3 0 0.1 0.2 0.3 0.4 0.5 0.6 I 0 / w max ( 2 |A(ωex)| ) γ / fex Numerical 1st osc. Numerical 2nd osc. Theory 1st osc. Theory 2nd osc. | f ex eff / (2 f ex )| Figure 4: Blue (green) dots show the normalized maximum of the oscillation amplitude for the first (second) oscillator as a function of the modulation amplitude I0/w. The solid lines show the result of an analytical calculation based on the rotating wave approximation (see text). System parameters as in Fig. 3. The dynamical decoupling seen in Fig. 3(b) corresponds here to the minimum of max(|A2|) that is visible around I0/w ≃ 1.2. The dynamical isolation seen in Fig. 3(c) lies in the vicinity of the simultaneous minima of both max(|A1,2|) that are visible around I0/w ≃ 2.4. In the fig￾ure, note the further dynamical decoupling point around I0/w ≃ 2.7. The solid lines are the analytical predictions of the rotating wave approximation that will be presented afterwards. Further insight on the effective coupling of the two pendulums, resulting from the temporal modulation, is given in Fig. 5. In panel (a) we present the numerically estimated magnitude of the effective coupling between the pendulums: this quantity is observable as the beat frequency in Fig. 2, or as the separation between peaks in the response spectra of Fig. 3. Most remarkable fea￾tures of Fig. 5(a) are the vanishing effective coupling at I0/w ≃ 1.2 and I0/w ≃ 2.7, corresponding to the zeros of only max(|A2|) in Fig. 4. In the following, we will see that these numerical values are related to the zeros of the zeroth-order Bessel function. Another crucial consequence of the temporal modula￾tion is shown in the lower panel Fig. 5(b). While the eigen￾modes of the bare system correspond to in-phase and out￾of-phase oscillations, the modulation allows to tune the relative phase of the oscillation of the two pendulums to any value from 0 to 2π. In mathematical terms, the effec￾tive coupling develops a non-trivial phase. Note how this phase displays π jumps whenever the effective coupling goes through zero. Before proceeding, it is worth noting in Fig. 3 a sizeable global shift of the resonance curves to￾wards lower frequencies for growing I0. An explanation 0 0.5 1 1.5 2 2.5 3 0 0.25 0.5 0.75 1 I 0 /w | Ωeff /Ω | 0 0.5 1 1.5 2 2.5 3 0 2 4 6 I 0 /w arg( Ωeff /Ω ) Numerical Theory (a) (b) Figure 5: Modulus of the effective coupling frequency |Ωeff|/Ω [upper (a) panel] and its phase arg(Ωeff) (modulo 2π) [lower (b) panel]. Dots are the results of the numerical calculations as dis￾cussed in the text, while the solid lines are analytical predictions of the RW approximation. System parameters as in Fig. 3. of this effect will be given in the next section. Analytical expressions within the rotating wave ap￾proximation. – Analytical insight in the physics of the modulated system can be obtained within the so-called rotating wave (RW) approximation, well-known from quantum optics. This approximation relies on assuming that the natural oscillation frequency ω0 is much larger than all other internal frequencies in the problem, that is ω0 ≫ max(Ω, γ, w, |ωex −ω0|). Since the α variables rotate at ≈ ω0 and their conjugate variables α ∗ rotate at ≈ −ω0, the RW approximation is straightforwardly implemented by neglecting the α ∗ terms in the motion Equations (10) for the α variables. To obtain an effective, temporally averaged form of the stroboscopic dynamics of the system, we introduce the new variables: βi(t) = αi(t) exp[i R t 0 vi(t ′ ) dt ′ ] exp[i ωext]. For the chosen sinusoidal form of the modulation, the phase factor involving the modulation is exactly equal to 1 at the stroboscopic times tj = 2πj/w that are considered in the figures. Since we are in the fast modulation regime w ≫ Ω, effective equations, which no longer depend on the time t, can be obtained [30] by averaging the RW form of the equations (10) over a modulation period T = 2π/w: β˙ 1 = −i (¯ω0 − ωex) β1 − γ β1 + i (Ωeff 12/2) β2 + if eff ex (11) β˙ 2 = −i (¯ω0 − ωex) β2 − γ β2 + i (Ωeff 21/2) β1. (12) The effective couplings in Eqs. (11)-(12) are defined by: Ω eff ij ≡ Ω T Z T 0 dt e i R t 0 [vi(t ′ )−vj (t ′ )] dt ′ and they are complex conjugate to each other, Ω eff 12 = Ωeff∗ 21 . p-4