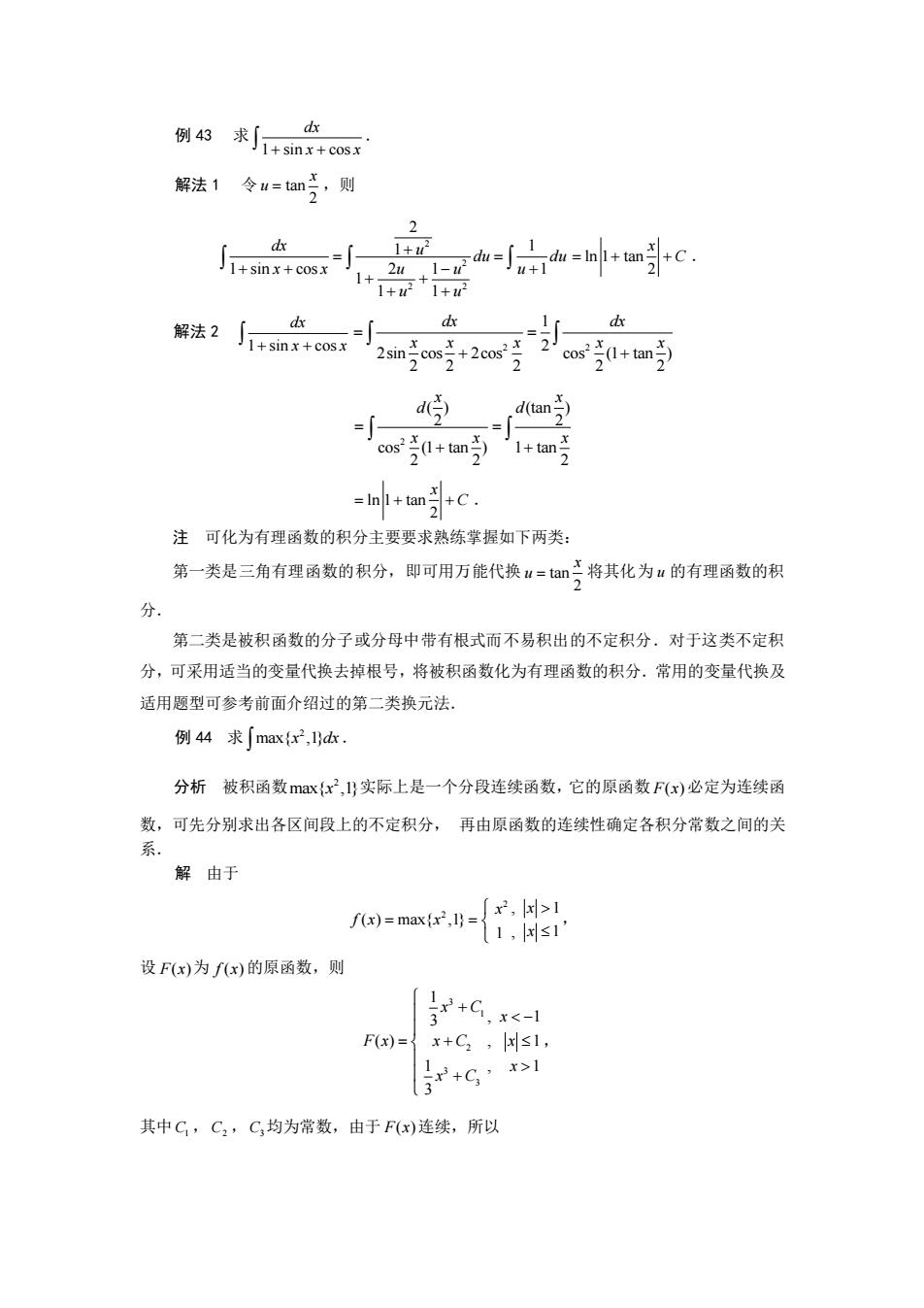
例相利产 解法1令u=tan芳，则 1++7+1+0 解法2+m+es d ow d2 d(tan) = cos(l+tan)1+tan =In1+tan+C. 注可化为有理函数的积分主要要求熟练掌握如下两类： 第一类是三角有理函数的积分，即可用万能代换u=tan将其化为的有理函数的积 分 第二类是被积函数的分子或分母中带有根式而不易积出的不定积分，对于这类不定积 分，可采用适当的变量代换去掉根号，将被积函数化为有理函数的积分。常用的变量代换及 适用题型可参考前面介绍过的第二类换元法. 例44求[max{x2,1d 分析被积函数maxx2,1)实际上是一个分段连续函数，它的原函数F(x)必定为连续函 数，可先分别求出各区间段上的不定积分，再由原函数的连续性确定各积分常数之间的关 解由于 )-mate 设F(x)为fx)的原函数，则 F(x)={x+C:,s1 +G 其中G,C2,C均为常数，由于F(x)连续，所以例 43 求 1 sin cos dx + +x x  ． 解法 1 令 tan 2 x u = ，则 2 2 2 2 2 1 1 1 sin cos 1 2 1 1 1 1 dx u du du x x u u u u u + = = + + + − + + + +    ln 1 tan 2 x = + + C ． 解法 2 1 sin cos dx + +x x  2 2 1 2 2sin cos 2cos cos (1 tan ) 2 2 2 2 2 dx dx x x x x x = = + +   2 ( ) (tan ) 2 2 cos (1 tan ) 1 tan 2 2 2 x x d d x x x = = + +   ln 1 tan 2 x = + + C ． 注 可化为有理函数的积分主要要求熟练掌握如下两类： 第一类是三角有理函数的积分，即可用万能代换 tan 2 x u = 将其化为 u 的有理函数的积 分． 第二类是被积函数的分子或分母中带有根式而不易积出的不定积分．对于这类不定积 分，可采用适当的变量代换去掉根号，将被积函数化为有理函数的积分．常用的变量代换及 适用题型可参考前面介绍过的第二类换元法． 例 44 求 2 max{ ,1} x dx  ． 分析 被积函数 2 max{ ,1} x 实际上是一个分段连续函数，它的原函数 F x( ) 必定为连续函 数，可先分别求出各区间段上的不定积分， 再由原函数的连续性确定各积分常数之间的关 系． 解 由于 2 2 , 1 ( ) max{ ,1} 1 , 1 x x f x x x   = =    ， 设 F x( ) 为 f x( ) 的原函数，则 3 1 2 3 3 1 3 , 1 ( ) , 1 1 , 1 3 x C x F x x C x x x C  +   −  = +      +  ， 其中 C1 ， C2 ，C3 均为常数，由于 F x( ) 连续，所以