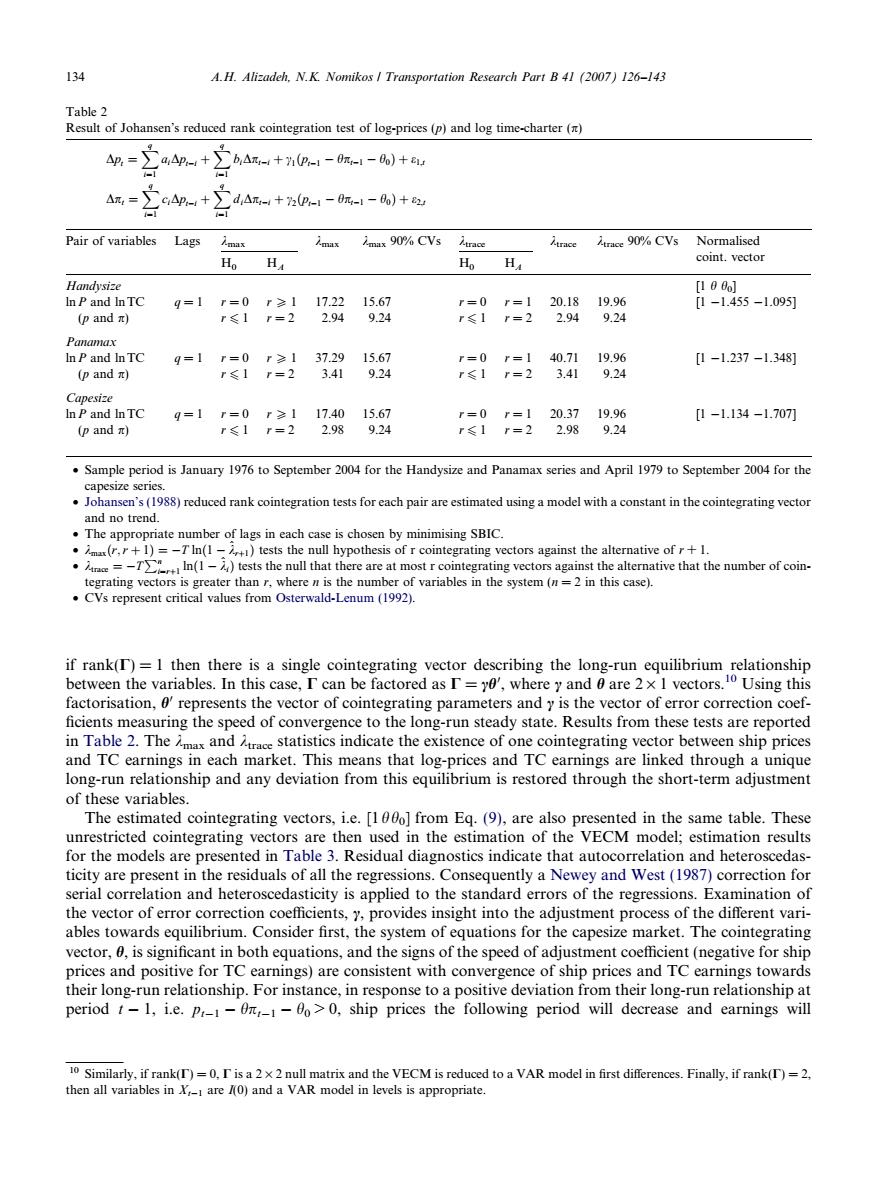
134 A.H.Alizadeh.N.K.Nomikos Transportation Research Part B 41 (2007)126-143 Table 2 Result of Johansen's reduced rank cointegration test of log-prices (p)and log time-charter ( △p= b△r-+P-1-0π-l-o)+r △= dA-+2p-1-m-l-0）+ Pair of variables Lags Amax imax 90%CVs Atrace Atrace Atrace 90%CVs Normalised Ho H Ho H coint.vector Handysize [100o] In P and InTC 9=1 r=0r≥1 17.22 15.67 r=0r=1 20.1819.96 [1-1.455-1.09) (pandπ) r≤1r=2 2.94 9.24 r<I r=2 2.94 9.24 Panamax In P and InTC 9=1r=0r≥137.29 15.67 r=0r=140.71 19.96 [1-1.237-1.348] (pandπ) P≤I r=2 3.41 9.24 r≤1 r=2 3.41 9.24 Capesize In P and InTC 9=1 r=0r≥117.4015.67 r=0 r=120.37 19.96 [1-1.134-1.707刀 (pandπ) r≤1r=2 2.98 9.24 r≤1r=2 2.98 9.24 Sample period is January 1976 to September 2004 for the Handysize and Panamax series and April 1979 to September 2004 for the capesize series. .Johansen's(1988)reduced rank cointegration tests for each pair are estimated using a model with a constant in the cointegrating vector and no trend. .The appropriate number of lags in each case is chosen by minimising SBIC. .m(r,r+1)=-TIn(1-)tests the null hypothesis of r cointegrating vectors against the alternative of r+1. TIn(1)tests the null that there are at most r cointegrating vectors against the alternative that the number of coin- tegrating vectors is greater than r,where n is the number of variables in the system(n=2 in this case). CVs represent critical values from Osterwald-Lenum (1992). if rank(T)=1 then there is a single cointegrating vector describing the long-run equilibrium relationship between the variables.In this case,I can be factored as I=y0,where y and 0 are 2x 1 vectors.10 Using this factorisation,0'represents the vector of cointegrating parameters and y is the vector of error correction coef- ficients measuring the speed of convergence to the long-run steady state.Results from these tests are reported in Table 2.Themax and race statistics indicate the existence of one cointegrating vector between ship prices and TC earnings in each market.This means that log-prices and TC earnings are linked through a unique long-run relationship and any deviation from this equilibrium is restored through the short-term adjustment of these variables. The estimated cointegrating vectors,i.e.[100o]from Eq.(9),are also presented in the same table.These unrestricted cointegrating vectors are then used in the estimation of the VECM model;estimation results for the models are presented in Table 3.Residual diagnostics indicate that autocorrelation and heteroscedas- ticity are present in the residuals of all the regressions.Consequently a Newey and West(1987)correction for serial correlation and heteroscedasticity is applied to the standard errors of the regressions.Examination of the vector of error correction coefficients,y,provides insight into the adjustment process of the different vari- ables towards equilibrium.Consider first,the system of equations for the capesize market.The cointegrating vector,0,is significant in both equations,and the signs of the speed of adjustment coefficient(negative for ship prices and positive for TC earnings)are consistent with convergence of ship prices and TC earnings towards their long-run relationship.For instance,in response to a positive deviation from their long-run relationship at period t-1,i.e.P-1-0,-1-00>0,ship prices the following period will decrease and earnings will 10 Similarly,if rank(T)=0.r is a 2x2 null matrix and the VECM is reduced to a VAR model in first differences.Finally,if rank(T)=2. then all variables in X-1 are /(0)and a VAR model in levels is appropriate.if rank(C) = 1 then there is a single cointegrating vector describing the long-run equilibrium relationship between the variables. In this case, C can be factored as C = ch0 , where c and h are 2 · 1 vectors.10 Using this factorisation, h0 represents the vector of cointegrating parameters and c is the vector of error correction coef- ficients measuring the speed of convergence to the long-run steady state. Results from these tests are reported in Table 2. The kmax and ktrace statistics indicate the existence of one cointegrating vector between ship prices and TC earnings in each market. This means that log-prices and TC earnings are linked through a unique long-run relationship and any deviation from this equilibrium is restored through the short-term adjustment of these variables. The estimated cointegrating vectors, i.e. [1h h0] from Eq. (9), are also presented in the same table. These unrestricted cointegrating vectors are then used in the estimation of the VECM model; estimation results for the models are presented in Table 3. Residual diagnostics indicate that autocorrelation and heteroscedas￾ticity are present in the residuals of all the regressions. Consequently a Newey and West (1987) correction for serial correlation and heteroscedasticity is applied to the standard errors of the regressions. Examination of the vector of error correction coefficients, c, provides insight into the adjustment process of the different vari￾ables towards equilibrium. Consider first, the system of equations for the capesize market. The cointegrating vector, h, is significant in both equations, and the signs of the speed of adjustment coefficient (negative for ship prices and positive for TC earnings) are consistent with convergence of ship prices and TC earnings towards their long-run relationship. For instance, in response to a positive deviation from their long-run relationship at period t 1, i.e. pt1 hpt1 h0 > 0, ship prices the following period will decrease and earnings will Table 2 Result of Johansen’s reduced rank cointegration test of log-prices (p) and log time-charter (p) Dpt ¼ Xq i¼1 aiDpti þXq i¼1 biDpti þ c1ðpt1 hpt1 h0Þ þ e1;t Dpt ¼ Xq i¼1 ciDpti þXq i¼1 diDpti þ c2ðpt1 hpt1 h0Þ þ e2;t Pair of variables Lags kmax kmax kmax 90% CVs ktrace ktrace ktrace 90% CVs Normalised coint. vector H0 HA H0 HA Handysize [1 h h0] lnP and lnTC q = 1 r = 0 r P 1 17.22 15.67 r = 0 r = 1 20.18 19.96 [1 1.455 1.095] (p and p) r 6 1 r = 2 2.94 9.24 r 6 1 r = 2 2.94 9.24 Panamax lnP and lnTC q = 1 r = 0 r P 1 37.29 15.67 r = 0 r = 1 40.71 19.96 [1 1.237 1.348] (p and p) r 6 1 r = 2 3.41 9.24 r 6 1 r = 2 3.41 9.24 Capesize lnP and lnTC q = 1 r = 0 r P 1 17.40 15.67 r = 0 r = 1 20.37 19.96 [1 1.134 1.707] (p and p) r 6 1 r = 2 2.98 9.24 r 6 1 r = 2 2.98 9.24 • Sample period is January 1976 to September 2004 for the Handysize and Panamax series and April 1979 to September 2004 for the capesize series. • Johansen’s (1988) reduced rank cointegration tests for each pair are estimated using a model with a constant in the cointegrating vector and no trend. • The appropriate number of lags in each case is chosen by minimising SBIC. • kmaxðr;r þ 1Þ¼T lnð1 ^krþ1Þ tests the null hypothesis of r cointegrating vectors against the alternative of r + 1. • ktrace ¼ T Pn i¼rþ1 lnð1 ^kiÞ tests the null that there are at most r cointegrating vectors against the alternative that the number of coin￾tegrating vectors is greater than r, where n is the number of variables in the system (n = 2 in this case). • CVs represent critical values from Osterwald-Lenum (1992). 10 Similarly, if rank(C) = 0, C is a 2 · 2 null matrix and the VECM is reduced to a VAR model in first differences. Finally, if rank(C) = 2, then all variables in Xt1 are I(0) and a VAR model in levels is appropriate. 134 A.H. Alizadeh, N.K. Nomikos / Transportation Research Part B 41 (2007) 126–143