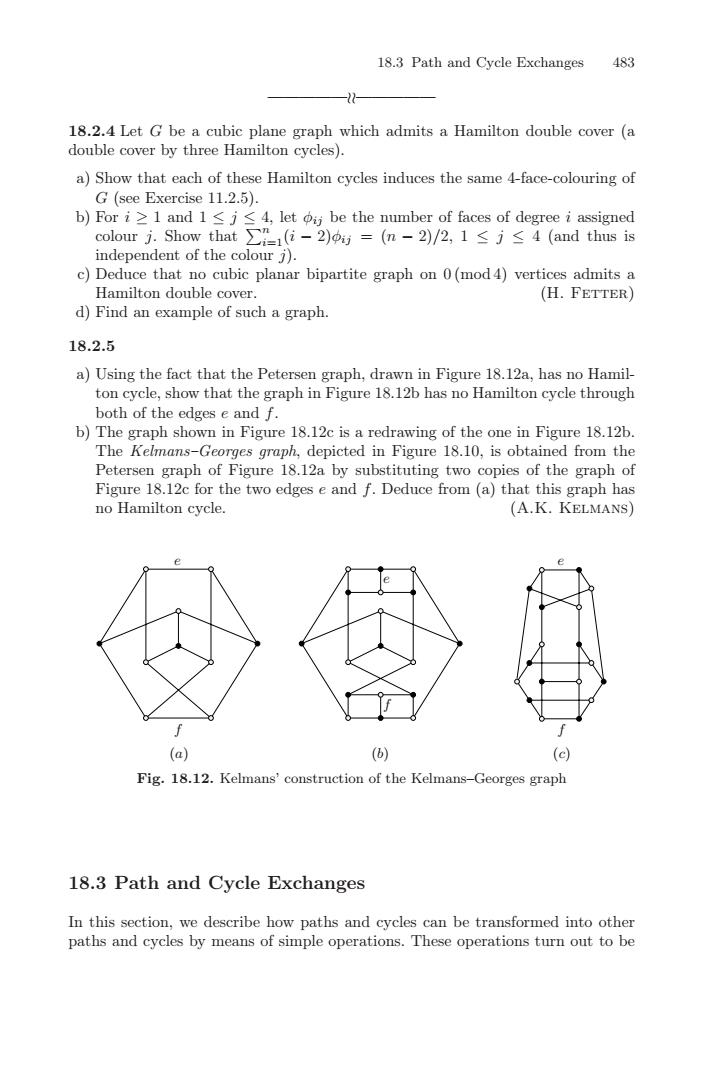
18.3 Path and Cycle Exchanges48318.2.4Let G bibicnlangraphwhichadmitsaHammilton doublecover (adouble cover by three Hamilton cycles).a) Show that each of these Hamilton cycles induces the same 4-face-colouring ofG (see Exercise 11.2.5)b) Fori≥l and 1≤j≤4, let piy be the number of faces of degreeiassignedcolour j. Show that r=1(i - 2)oij = (n -2)/2, 1 ≤ j ≤4 (and thus isindependent of the colour j)c) Deduce that no cubic planar bipartite graph on 0(mod4) vertices admits Hamilton doublecover(H.FETTER)d) Find an example of such a graph18.2.5a) Using the fact that the Petersen graph, drawn in Figure 18.12a, has no Hamil.ton cycle,showthatthlegraphinFigure18.12bhasnoHamiltoncyclethroughboth of the edges eandfb) The graph shown in Figure 18.12c is a redrawing of the one in Figure 18.12b.The Kelmans-Georges graph, depicted in Figure 18.10, is obtained from thePetersen graph of Figure 18.12a by substituting two copies of the graph ofFigure 18.12c for the two edges e and f. Deduce from (a) that this graph hasnoHamiltoncycle(A.K. KELMANS)佳(a) (b)Fig. 18.12. Kelmconstruction of the Kelmans-Georges graph18.3 Path and Cycle ExchangesIn this section, we describe how paths and cycles can be transformed into otherpaths and cycles by means of simple operations.These operations turn out to be18.3 Path and Cycle Exchanges 483 ————— ————— 18.2.4 Let G be a cubic plane graph which admits a Hamilton double cover (a double cover by three Hamilton cycles). a) Show that each of these Hamilton cycles induces the same 4-face-colouring of G (see Exercise 11.2.5). b) For i ≥ 1 and 1 ≤ j ≤ 4, let φij be the number of faces of degree i assigned colour j. Show that
n i=1(i − 2)φij = (n − 2)/2, 1 ≤ j ≤ 4 (and thus is independent of the colour j). c) Deduce that no cubic planar bipartite graph on 0(mod 4) vertices admits a Hamilton double cover. (H. Fetter) d) Find an example of such a graph. 18.2.5 a) Using the fact that the Petersen graph, drawn in Figure 18.12a, has no Hamil￾ton cycle, show that the graph in Figure 18.12b has no Hamilton cycle through both of the edges e and f. b) The graph shown in Figure 18.12c is a redrawing of the one in Figure 18.12b. The Kelmans–Georges graph, depicted in Figure 18.10, is obtained from the Petersen graph of Figure 18.12a by substituting two copies of the graph of Figure 18.12c for the two edges e and f. Deduce from (a) that this graph has no Hamilton cycle. (A.K. Kelmans) (a) (b) (c) e e e f f f Fig. 18.12. Kelmans’ construction of the Kelmans–Georges graph 18.3 Path and Cycle Exchanges In this section, we describe how paths and cycles can be transformed into other paths and cycles by means of simple operations. These operations turn out to be