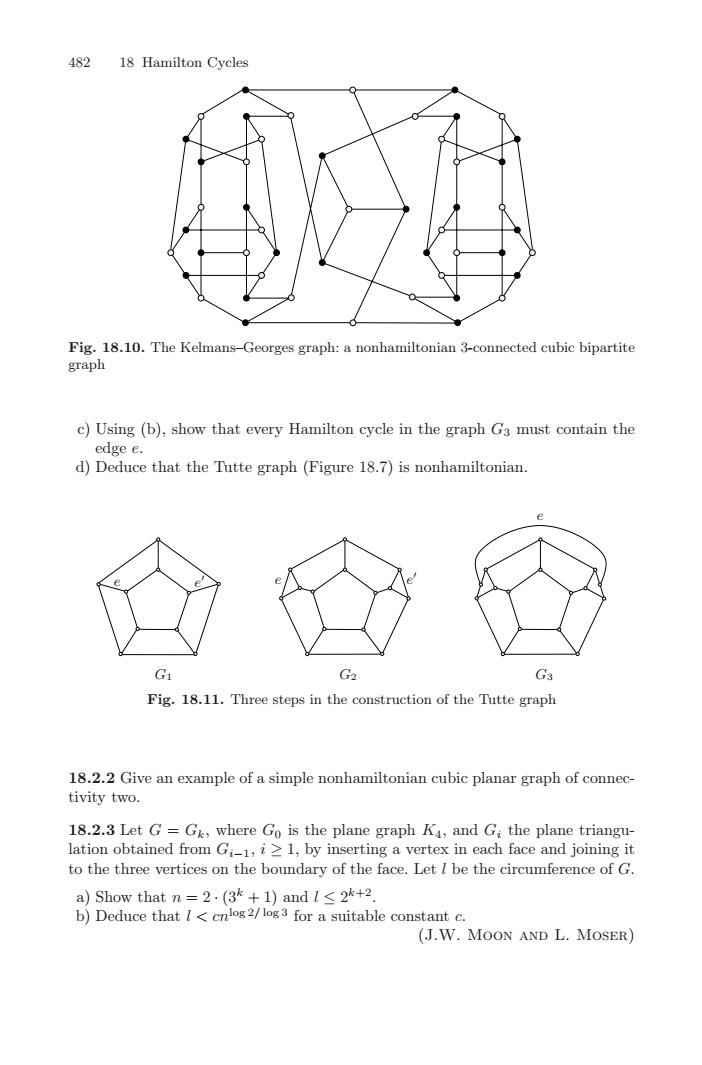
482181Fig. 18.10. The Kelectedcubicbipartiteesgraph:aneerapc) Using (b), show that every Hamilton cycle in the graph G3 must contain theedgeed) Deduce that the Tutte graph (Figure 18.7) is nonhamiltonian.G1G2GFig. 18.11. Threof the Tutte graphteosThecons18.2.2 Give pleofasimplenonacubicgraphofcoltoniativity two.18.2.3Let G =G, where Go is the plane graph Ka,and G, the plane triangulation obtained from Gi-1, i ≥ 1, by inserting a vertex in each face and joining ittothe three vertices on theboumdaryoftheface.LetIbe the circumference ofG.a) Show that n =2. (3*+ 1) and 1≤2k+2.b) Deduce that l < cnlog2/ log 3 for a suitable constant(J.W. MOON AND L. MOSER)482 18 Hamilton Cycles Fig. 18.10. The Kelmans–Georges graph: a nonhamiltonian 3-connected cubic bipartite graph c) Using (b), show that every Hamilton cycle in the graph G3 must contain the edge e. d) Deduce that the Tutte graph (Figure 18.7) is nonhamiltonian. e e e e
e
G1 G2 G3 Fig. 18.11. Three steps in the construction of the Tutte graph 18.2.2 Give an example of a simple nonhamiltonian cubic planar graph of connec￾tivity two. 18.2.3 Let G = Gk, where G0 is the plane graph K4, and Gi the plane triangu￾lation obtained from Gi−1, i ≥ 1, by inserting a vertex in each face and joining it to the three vertices on the boundary of the face. Let l be the circumference of G. a) Show that n = 2 · (3k + 1) and l ≤ 2k+2. b) Deduce that l < cnlog 2/ log 3 for a suitable constant c. (J.W. Moon and L. Moser)