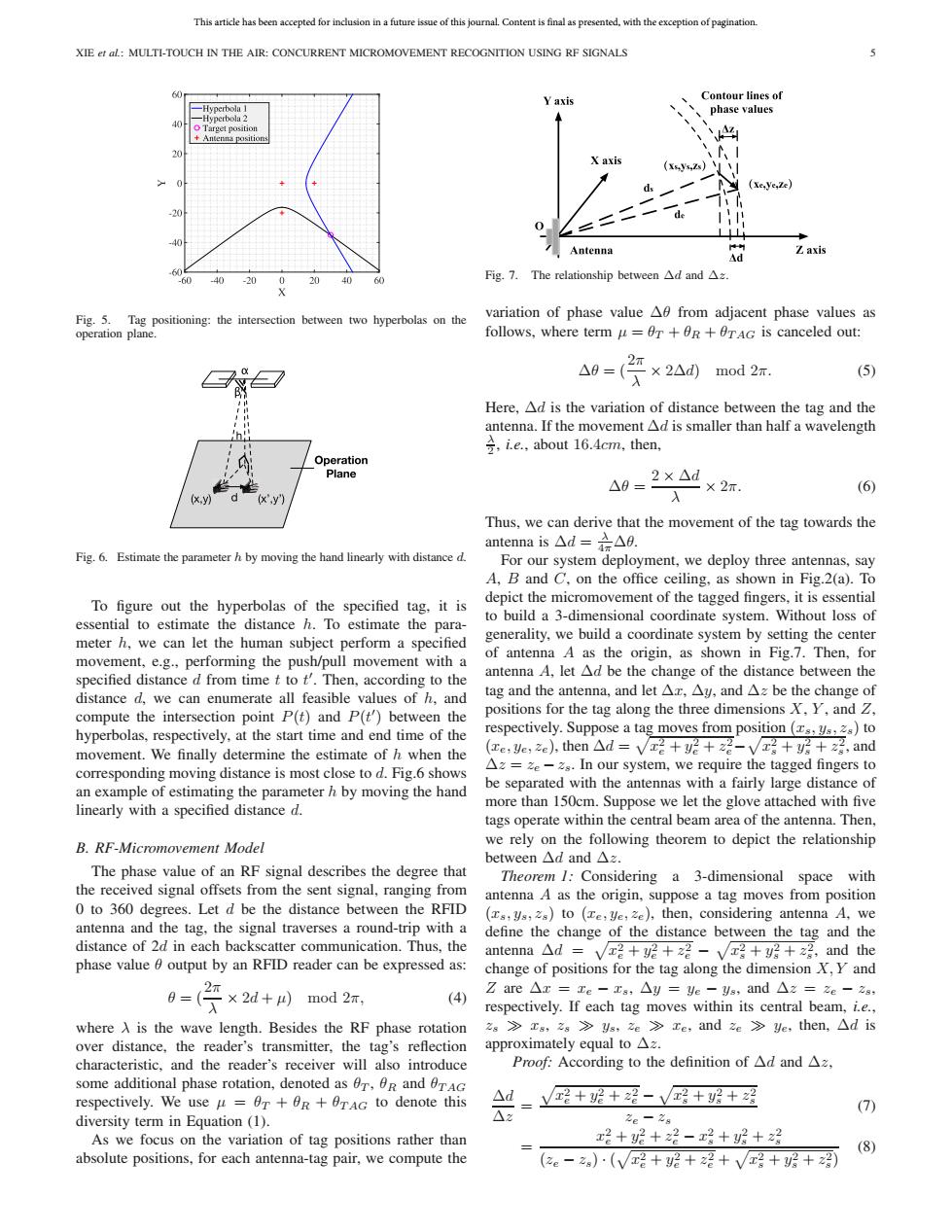
This article has been accepted for inclusion in a future issue of this journal.Content is final as presented,with the exception of pagination. XIE et al:MULTI-TOUCH IN THE AIR:CONCURRENT MICROMOVEMENT RECOGNITION USING RF SIGNALS 60 Yaxis Contour lines of 一Hyperbola 1 `、phase values -Hyperbola 2 Target position Antenna position 、、 X axis (xsys,zs)\ ds Ny(xeye,Ze） de 0 1 /Antenna 例 △d Z axis 20 Fig.7.The relationship between△dand△z. Fig.5.Tag positioning:the intersection between two hyperbolas on the variation of phase value A from adjacent phase values as operation plane. follows,where term u=0r+0R+TAc is canceled out: △0= ·×2△d)mod2π (5) Here,Ad is the variation of distance between the tag and the antenna.If the movement Ad is smaller than half a wavelength ≥，ie,about 16.4cm,then, Operation Plane △8= 2×△d ×2π」 (6) X V 入 Thus,we can derive that the movement of the tag towards the antenna is△d=六△， Fig.6.Estimate the parameter h by moving the hand linearly with distance d. For our system deployment,we deploy three antennas,say A,B and C.on the office ceiling,as shown in Fig.2(a).To To figure out the hyperbolas of the specified tag,it is depict the micromovement of the tagged fingers,it is essential essential to estimate the distance h.To estimate the para- to build a 3-dimensional coordinate system.Without loss of meter h,we can let the human subject perform a specified generality,we build a coordinate system by setting the center movement,e.g.,performing the push/pull movement with a of antenna A as the origin,as shown in Fig.7.Then,for specified distance d from time t to t'.Then,according to the antenna A,let Ad be the change of the distance between the distance d,we can enumerate all feasible values of h,and tag and the antenna,.and let△x,△y,and△e be the change of compute the intersection point P(t)and P(t')between the positions for the tag along the three dimensions X.Y,and Z, hyperbolas,respectively,at the start time and end time of the respectively.Suppose a tag moves from position (s,4s,2)to movement.We finally determine the estimate of h when the (re:e,ze),then△d=V√径+y+z径-√g+y+z径，and corresponding moving distance is most close to d.Fig.6 shows Az=ze-2s.In our system,we require the tagged fingers to an example of estimating the parameter h by moving the hand be separated with the antennas with a fairly large distance of linearly with a specified distance d. more than 150cm.Suppose we let the glove attached with five tags operate within the central beam area of the antenna.Then, B.RF-Micromovement Model we rely on the following theorem to depict the relationship between△dand△z. The phase value of an RF signal describes the degree that Theorem 1:Considering a 3-dimensional space with the received signal offsets from the sent signal,ranging from antenna A as the origin,suppose a tag moves from position 0 to 360 degrees.Let d be the distance between the RFID (s,ys,2s)to (e,ye,ze),then,considering antenna A,we antenna and the tag,the signal traverses a round-trip with a define the change of the distance between the tag and the distance of 2d in each backscatter communication.Thus,the antenna△d=vc+y+2径-√rg+y好+2径，and the phase value 0 output by an RFID reader can be expressed as: change of positions for the tag along the dimension X,Y and ×2d+4）mod2π (4) Zare△x=re-ra,△y=ye-ys,and△z=ze-zs: respectively.If each tag moves within its central beam,i.e., where A is the wave length.Besides the RF phase rotation 2s s,2s>ys.ze e,and ze ye,then.Ad is over distance,the reader's transmitter,the tag's reflection approximately equal to Az. characteristic,and the reader's receiver will also introduce Proof:According to the definition of△dand△z, some additional phase rotation,denoted as er,OR and rAc respectively.We use u=0T+0R+rAc to denote this △d 哈+呢+2是-+班+图 (7) diversity term in Equation(1). △z 2e-2s As we focus on the variation of tag positions rather than x2+呢+是-x?++2 (8) absolute positions,for each antenna-tag pair,we compute the (2e-)·(√哈+经+径+√号+好+)This article has been accepted for inclusion in a future issue of this journal. Content is final as presented, with the exception of pagination. XIE et al.: MULTI-TOUCH IN THE AIR: CONCURRENT MICROMOVEMENT RECOGNITION USING RF SIGNALS 5 Fig. 5. Tag positioning: the intersection between two hyperbolas on the operation plane. Fig. 6. Estimate the parameter h by moving the hand linearly with distance d. To figure out the hyperbolas of the specified tag, it is essential to estimate the distance h. To estimate the para￾meter h, we can let the human subject perform a specified movement, e.g., performing the push/pull movement with a specified distance d from time t to t . Then, according to the distance d, we can enumerate all feasible values of h, and compute the intersection point P(t) and P(t ) between the hyperbolas, respectively, at the start time and end time of the movement. We finally determine the estimate of h when the corresponding moving distance is most close to d. Fig.6 shows an example of estimating the parameter h by moving the hand linearly with a specified distance d. B. RF-Micromovement Model The phase value of an RF signal describes the degree that the received signal offsets from the sent signal, ranging from 0 to 360 degrees. Let d be the distance between the RFID antenna and the tag, the signal traverses a round-trip with a distance of 2d in each backscatter communication. Thus, the phase value θ output by an RFID reader can be expressed as: θ = (2π λ × 2d + μ) mod 2π, (4) where λ is the wave length. Besides the RF phase rotation over distance, the reader’s transmitter, the tag’s reflection characteristic, and the reader’s receiver will also introduce some additional phase rotation, denoted as θT , θR and θT AG respectively. We use μ = θT + θR + θT AG to denote this diversity term in Equation (1). As we focus on the variation of tag positions rather than absolute positions, for each antenna-tag pair, we compute the Fig. 7. The relationship between Δd and Δz. variation of phase value Δθ from adjacent phase values as follows, where term μ = θT + θR + θT AG is canceled out: Δθ = (2π λ × 2Δd) mod 2π. (5) Here, Δd is the variation of distance between the tag and the antenna. If the movement Δd is smaller than half a wavelength λ 2 , i.e., about 16.4cm, then, Δθ = 2 × Δd λ × 2π. (6) Thus, we can derive that the movement of the tag towards the antenna is Δd = λ 4πΔθ. For our system deployment, we deploy three antennas, say A, B and C, on the office ceiling, as shown in Fig.2(a). To depict the micromovement of the tagged fingers, it is essential to build a 3-dimensional coordinate system. Without loss of generality, we build a coordinate system by setting the center of antenna A as the origin, as shown in Fig.7. Then, for antenna A, let Δd be the change of the distance between the tag and the antenna, and let Δx, Δy, and Δz be the change of positions for the tag along the three dimensions X, Y , and Z, respectively. Suppose a tag moves from position (xs, ys, zs) to (xe, ye, ze), then Δd = x2 e + y2 e + z2 e− x2 s + y2 s + z2 s , and Δz = ze − zs. In our system, we require the tagged fingers to be separated with the antennas with a fairly large distance of more than 150cm. Suppose we let the glove attached with five tags operate within the central beam area of the antenna. Then, we rely on the following theorem to depict the relationship between Δd and Δz. Theorem 1: Considering a 3-dimensional space with antenna A as the origin, suppose a tag moves from position (xs, ys, zs) to (xe, ye, ze), then, considering antenna A, we define the change of the distance between the tag and the antenna Δd = x2 e + y2 e + z2 e − x2 s + y2 s + z2 s , and the change of positions for the tag along the dimension X, Y and Z are Δx = xe − xs, Δy = ye − ys, and Δz = ze − zs, respectively. If each tag moves within its central beam, i.e., zs  xs, zs  ys, ze  xe, and ze  ye, then, Δd is approximately equal to Δz. Proof: According to the definition of Δd and Δz, Δd Δz = x2 e + y2 e + z2 e − x2 s + y2 s + z2 s ze − zs (7) = x2 e + y2 e + z2 e − x2 s + y2 s + z2 s (ze − zs) · ( x2 e + y2 e + z2 e + x2 s + y2 s + z2 s ) (8)