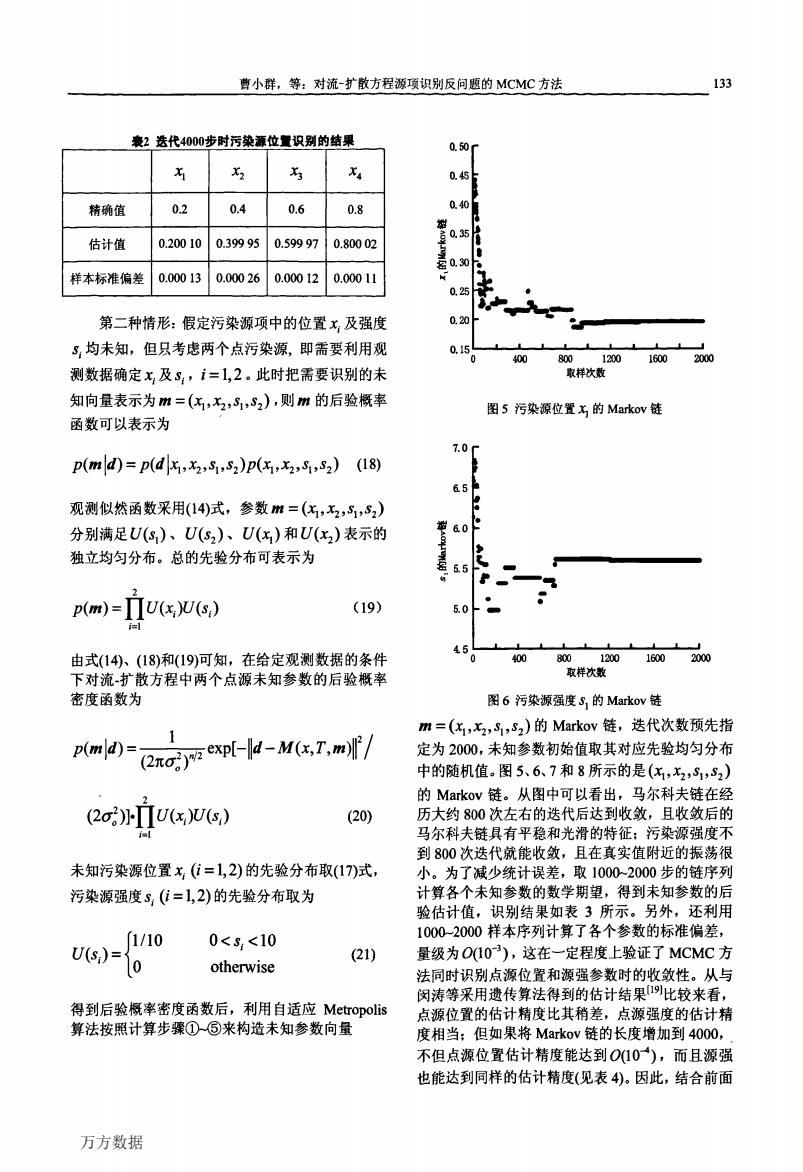
曹小群，等：对流-扩散方程源项识别反问题的MCMC方法 133 表2选代4000步时污染源位置识别的结果 3 0.45 精确值 0.2 0.4 0.6 0.8 0.40 035 估计值 0.20010 0.39995 0.59997 0.80002 030 样本标准偏差 0.00013 0.00026 0.00012 0.00011 0.25 第二种情形：假定污染源项中的位置x,及强度 020 3,均未知，但只考虑两个点污染源，即需要利用观 0.1 400 800120016002000 测数据确定x及，i=1,2。此时把需要识别的未 取样次数 知向量表示为m=(:,x2,1,S2),则m的后验概率 图5污染源位置方的Markov链 函数可以表示为 7.0 p(md)=p(d,x2,1,S2)p(x1,x2,,S2)(18) 65 观测似然函数采用(14)式，参数m=(:,x2,S,S2) 分别满足U(s)、U(s2)、U(:)和U(x)表示的 ao 独立均匀分布。总的先验分布可表示为 p(m)=IIU(X(s) (19) 5.0 由式(14)、(18)和(19)可知，在给定观测数据的条件 00 8001200 16002000 下对流-扩散方程中两个点源未知参数的后验概率 取样次数 密度函数为 图6污染源强度S,的Markov链 m=(1,x2,S,S2)的Markov链，迭代次数预先指 p(mld)-2yexpt--M(.T.m)/ 定为2000，未知参数初始值取其对应先验均匀分布 中的随机值。图5、6、7和8所示的是(：1，x2,S1,S2) 的Markov链。从图中可以看出，马尔科夫链在经 (2U(U(s) (20) 历大约800次左右的迭代后达到收敛，且收敛后的 马尔科夫链具有平稳和光滑的特征：污染源强度不 到800次迭代就能收敛，且在真实值附近的振荡很 未知污染源位置x(i=1,2)的先验分布取(17)式， 小。为了减少统计误差，取1000-2000步的链序列 污染源强度5，(i=1,2)的先验分布取为 计算各个未知参数的数学期望，得到未知参数的后 验估计值，识别结果如表3所示。另外，还利用 1/10 Us)=0 0<3,<10 1000-2000样本序列计算了各个参数的标准偏差， (21) 量级为O103),这在一定程度上验证了MCMC方 otherwise 法同时识别点源位置和源强参数时的收敛性。从与 闵涛等采用遗传算法得到的估计结果比较来看， 得到后验概率密度函数后，利用自适应Metropolis 点源位置的估计精度比其稍差，点源强度的估计精 算法按照计算步骤①⑤来构造未知参数向量 度相当：但如果将Markov链的长度增加到4000， 不但点源位置估计精度能达到O10),而且源强 也能达到同样的估计精度（见表4）。因此，结合前面 万方数据曹小群，等：对流一扩散方程源项识别反问题的McMc方法 五 恐 屯 矗 精确值 O．2 0．4 0．6 0．8 估计值 0．200 10 O．399 95 O．59997 0．80002 样本标准偏差 0．000 13 O．00026 O．000 12 0．ooOll 第二种情形：假定污染源项中的位置五及强度 量均未知，但只考虑两个点污染源，即需要利用观 测数据确定五及墨，f=1，2。此时把需要识别的未 知向量表示为朋=(五，屯，Jl，s2)，则朋的后验概率 函数可以表示为 。 p(肌ld)=p(dljcl，恐，sl，s2)p(_，jc2，sl，s2) (18) 观测似然函数采用(14)式，参数朋=(五，恐，■，s2) 分别满足【，(量)、U(s2)、U(五)和U(而)表示的 独立均匀分布。总的先验分布可表示为 (19) 由式(14)、(18)和(19)可知，在给定观测数据的条件 下对流．扩散方程中两个点源未知参数的后验概率 密度函数为 咖护面知eXp[一卜M(妒圳2／ 一 2 (2《)】．兀u(五)u(墨) (20) f=I 未知污染源位置薯(f=l，2)的先验分布取(17)式， 污染源强度s，(f=l，2)的先验分布取为 fl／10 叭墨户佰 0<s：<10 oth未ise (21) 得到后验概率密度函数后，利用自适应Me仃opolis 算法按照计算步骤∞来构造未知参数向量 0．的 o．45 o．20 o．15 7．0 矗5 掣＆o 墨 皇 g 5．5 5．0 生5 O 400 8∞ 1200 1600 2咖 取样次数 图5污染源位置五的Markov链 0 400 800 1200 1600 2000 取样次数 图6污染源强度sl的MarkoV链 133 朋=(五，五，s，岛)的Markov链，迭代次数预先指 定为2000，未知参数初始值取其对应先验均匀分布 中的随机值。图5、6、7和8所示的是(五，％，量，s，) 的Markov链。从图中可以看出，马尔科夫链在经 历大约800次左右的迭代后达到收敛，且收敛后的 马尔科夫链具有平稳和光滑的特征；污染源强度不 到800次迭代就能收敛，且在真实值附近的振荡很 小。为了减少统计误差，取1000~2000步的链序列 计算各个未知参数的数学期望，得到未知参数的后 验估计值，识别结果如表3所示。另外，还利用 1000乏000样本序列计算了各个参数的标准偏差， 量级为D(10一3)，这在一定程度上验证了McMC方 法同时识别点源位置和源强参数时的收敛性。从与 闵涛等采用遗传算法得到的估计结剁19J比较来看， 点源位置的估计精度比其稍差，点源强度的估计精 度相当；但如果将Markov链的长度增加到4000， 不但点源位置估计精度能达到D(10一)，而且源强 也能达到同样的估计精度(见表4)。因此，结合前面 ∞ ：穹 ∞ 龉 n n n n 端，卫皇‘宅．k U 薯 、， U0 、， ：n阿 lI p，L 肼 、， 万方数据