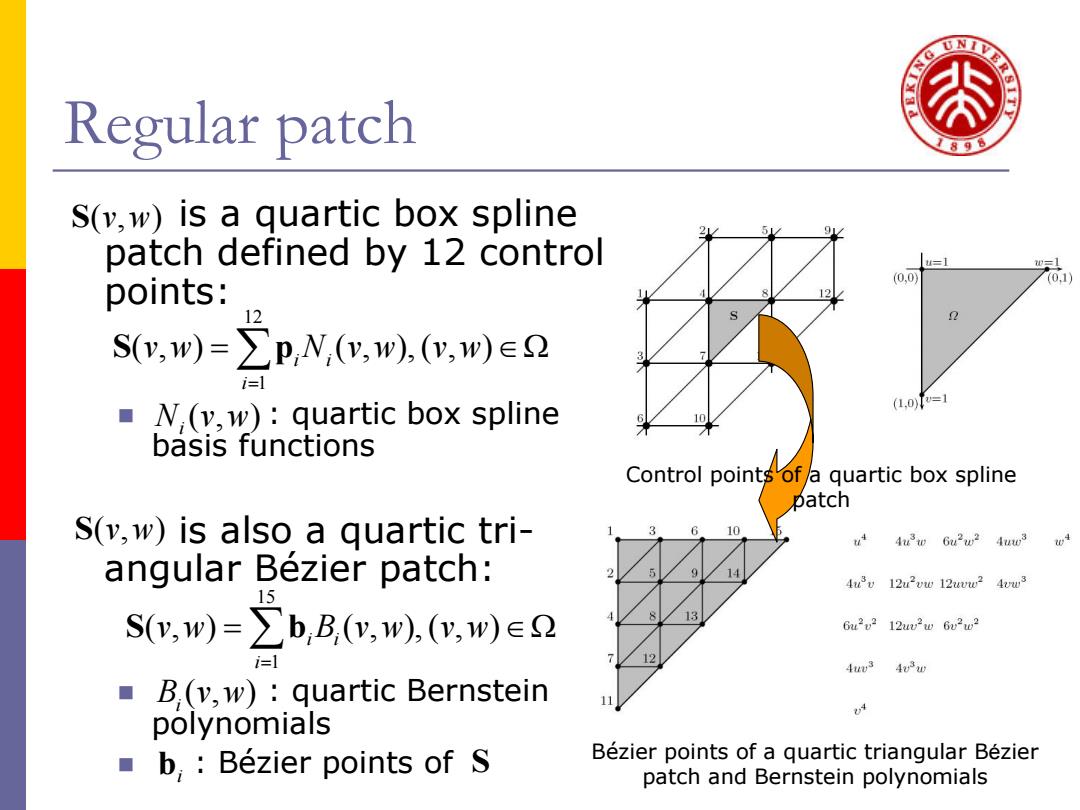
Regular patch S(v,w)is a quartic box spline patch defined by 12 control points: S(y,w)=∑P,N,(,w),(,w)）∈2 i=1 N,(v,w):quartic box spline basis functions Control points of a quartic box spline patch S(v,w)is also a quartic tri- u Aue Guu?Auw angular Bezier patch: 4v 12uww 12wu?Avw 15 S(y,w)=∑b,B(y,w),(y,w)∈2 6e2v212a2p62w2 Au 4w B(v,w):quartic Bernstein polynomials ■b,:Bezier points of S Bezier points of a quartic triangular Bezier patch and Bernstein polynomials Regular patch is a quartic box spline patch defined by 12 control points: „ : quartic box spline basis functions is also a quartic tri￾angular Bézier patch: „ : quartic Bernstein polynomials „ : Bézier points of S(, ) v w 12 1 ( , ) ( , ), ( , ) i i i vw N vw vw = S p = ∈ ∑ Ω S(, ) v w 15 1 ( , ) ( , ), ( , ) i i i vw B vw vw = S b = ∈ ∑ Ω Bézier points of a quartic triangular B ézier patch and Bernstein polynomials Control points of a quartic box spline patch (, ) N vw i (, ) Bi v w bi S