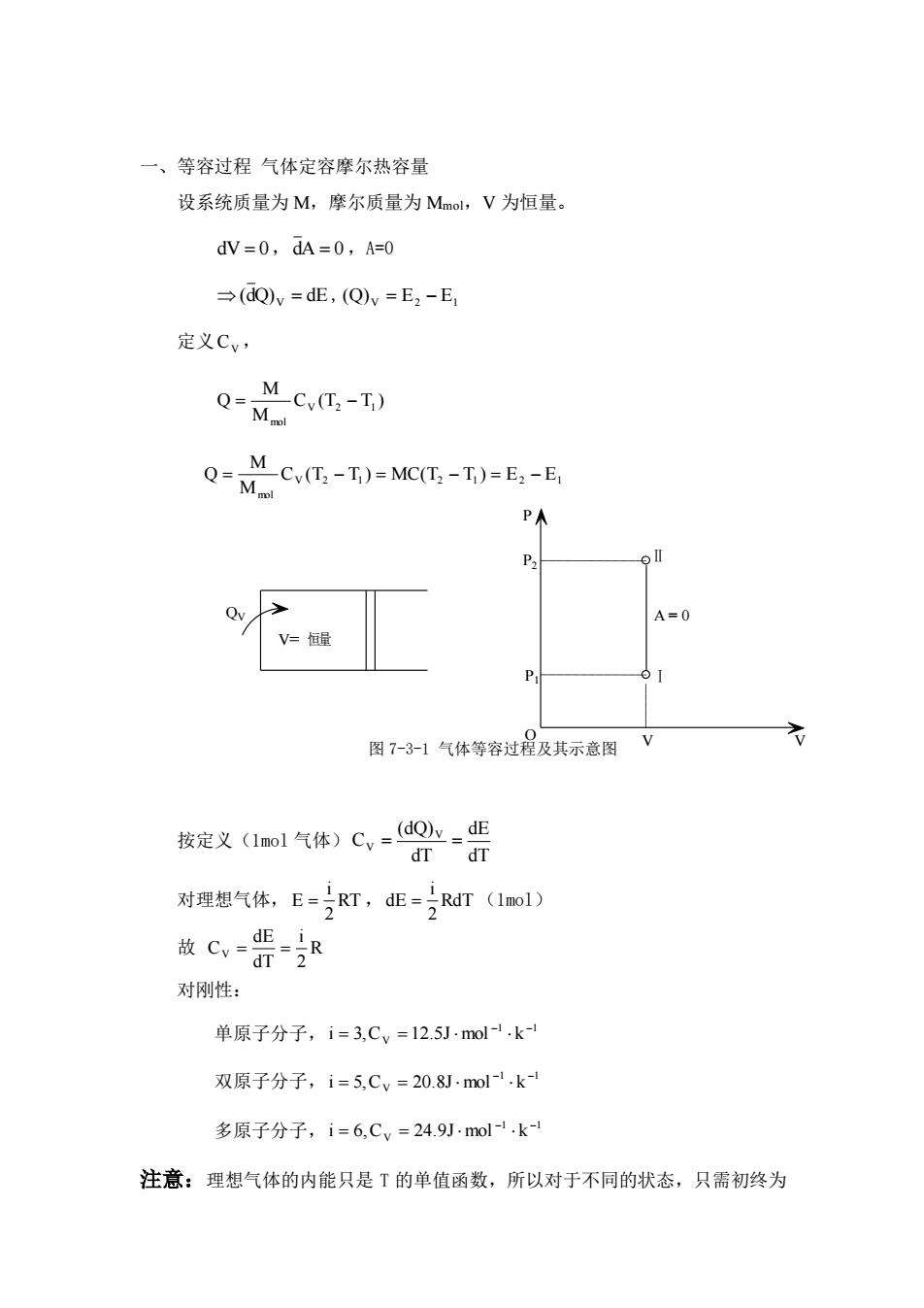
一、等容过程气体定容摩尔热容量 设系统质量为M,摩尔质量为Mml,V为恒量。 dV=0,dA=0,A=0 →(dQv=dE,(Q)v=E2-E, 定义Cv, -c.t,-T) Qc-0=c-0=-E PA 图7-3-1气体等容过程及其示意图V 按定义(1no1气体)Cv=do=dE dr dT 对理想气体，E=RT,d正=号RdT(1mol) 放c,普 对刚性： 单原子分子，i=3,Cv=12.5mol-.k- 双原子分子，i=5,Cv=20.8Jmol1.k 多原子分子，i=6,Cy=24.9mol-1.k 注意：理想气体的内能只是T的单值函数，所以对于不同的状态，只需初终为 一、等容过程 气体定容摩尔热容量 设系统质量为 M，摩尔质量为 Mmol，V 为恒量。 dV = 0，dA = 0，A=0  (dQ)V = dE , V E2 E1 (Q) = − 定义 CV ， C (T T ) M M Q V 2 1 mol = − V 2 1 2 1 2 1 mol C (T T ) MC(T T ) E E M M Q = − = − = − 图 7-3-1 气体等容过程及其示意图 按定义（1mol 气体） dT dE dT (dQ) C V V = = 对理想气体， RT 2 i E = ， RdT 2 i dE = （1mol） 故 R 2 i dT dE CV = = 对刚性： 单原子分子， 1 1 i 3,CV 12.5J mol k − − = =   双原子分子， 1 1 i 5,CV 20.8J mol k − − = =   多原子分子， 1 1 i 6,CV 24.9J mol k − − = =   注意：理想气体的内能只是 T 的单值函数，所以对于不同的状态，只需初终为 V＝ 恒量 QV P2 P1 P O V V A = 0 Ⅱ Ⅰ