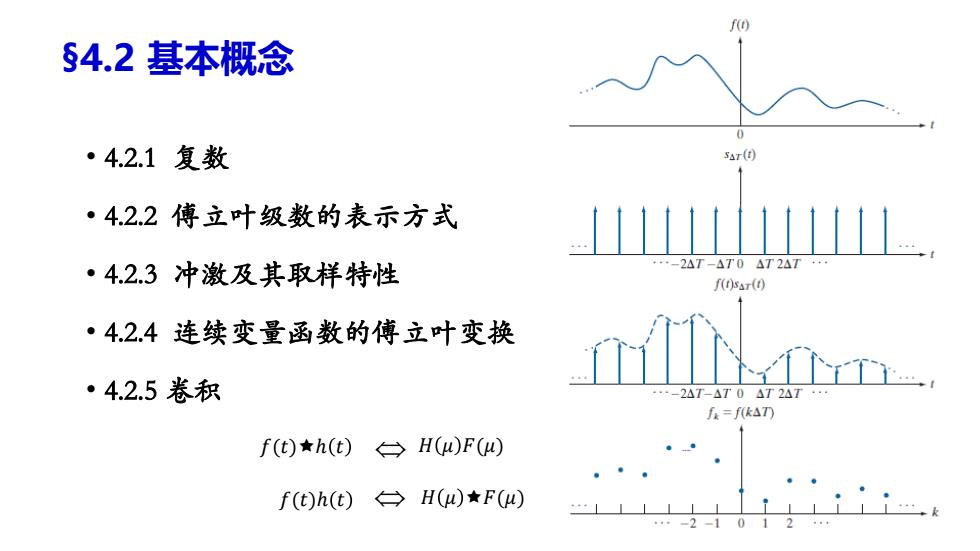
f() §4.2基本概念 ·4.2.1复数 SAr(t) ·4.2.2傅立叶级数的表示方式 ·4.2.3冲激及其取样特性 ·-2△T-△T0AT2AT·· f()ssr(t) ·4.2.4连续变量函数的傅立叶变换 ·4.2.5卷积 ·-2△T-△T0AT2AT f=fk△T刀 f(t)★h(t)台H(u)F() f(t)h(t)→H(a)★F(o) ···-2-1012 • 4.2.1 复数 • 4.2.2 傅立叶级数的表示方式 • 4.2.3 冲激及其取样特性 • 4.2.4 连续变量函数的傅立叶变换 • 4.2.5 卷积 ( , ) R I Real Imag(j) R I 傅立叶级数复数形式: 𝑓(𝑥) = ෍ 𝑛=−∞ ∞ 𝑐𝑛𝑒 𝑖 𝑛𝜋𝑥 𝑙 𝑓 𝑡 = න −∞ ∞ 𝐹 𝜇 𝑒 𝑗2𝜋𝜇𝑡𝑑𝜇 𝐹 𝜇 = න −∞ ∞ 𝑓(𝑡)𝑒 −𝑗2𝜋𝜇𝑡𝑑𝑡 傅里叶变换形式: 𝑓(𝑡)ℎ 𝑡  𝐻 𝜇 𝐹(𝜇) 𝑓(𝑡)ℎ 𝑡  𝐻 𝜇 𝐹(𝜇) §4.2 基本概念