《数字图像处理》课程教学课件（Digital Image Processing）频率域滤波 4.2 基本概念

频率域滤波 ·4.1背景 ·4.2基本概念 ·4.3取样和取样函数的傅立叶变换 ·4.4单变量的离散傅立叶变换 ·4.5两个变量的扩展 ·4.6二维离散傅立叶变换的一些性质 ·4.7频率域滤波基础 ·4.8频率域滤波器平滑图像 ·4.9频率域滤波器锐化图像 ·4.10选择性滤波

• 4.1 背景 • 4.2 基本概念 • 4.3 取样和取样函数的傅立叶变换 • 4.4 单变量的离散傅立叶变换 • 4.5 两个变量的扩展 • 4.6 二维离散傅立叶变换的一些性质 • 4.7 频率域滤波基础 • 4.8 频率域滤波器平滑图像 • 4.9 频率域滤波器锐化图像 • 4.10 选择性滤波 频率域滤波

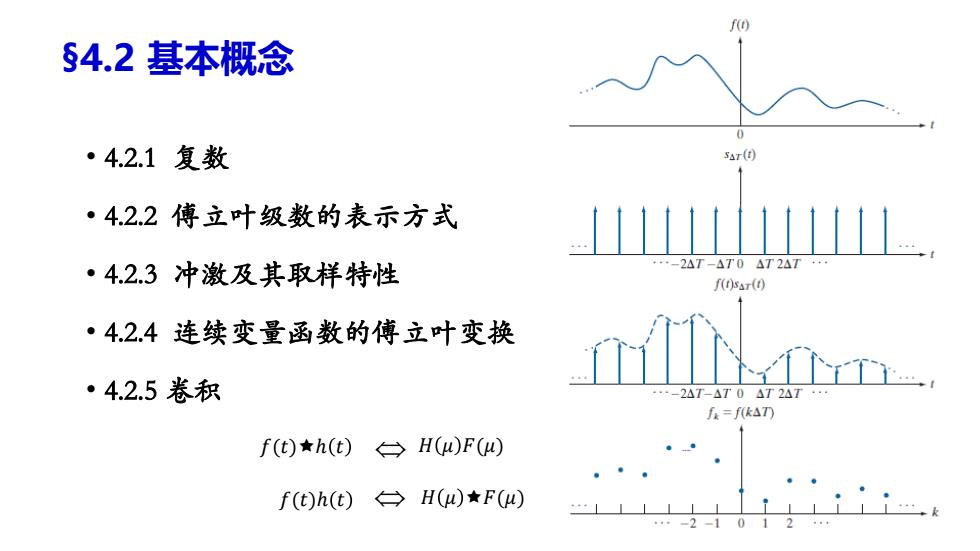
f() §4.2基本概念 ·4.2.1复数 SAr(t) ·4.2.2傅立叶级数的表示方式 ·4.2.3冲激及其取样特性 ·-2△T-△T0AT2AT·· f()ssr(t) ·4.2.4连续变量函数的傅立叶变换 ·4.2.5卷积 ·-2△T-△T0AT2AT f=fk△T刀 f(t)★h(t)台H(u)F() f(t)h(t)→H(a)★F(o) ···-2-1012

• 4.2.1 复数 • 4.2.2 傅立叶级数的表示方式 • 4.2.3 冲激及其取样特性 • 4.2.4 连续变量函数的傅立叶变换 • 4.2.5 卷积 ( , ) R I Real Imag(j) R I 傅立叶级数复数形式: 𝑓(𝑥) = ෍ 𝑛=−∞ ∞ 𝑐𝑛𝑒 𝑖 𝑛𝜋𝑥 𝑙 𝑓 𝑡 = න −∞ ∞ 𝐹 𝜇 𝑒 𝑗2𝜋𝜇𝑡𝑑𝜇 𝐹 𝜇 = න −∞ ∞ 𝑓(𝑡)𝑒 −𝑗2𝜋𝜇𝑡𝑑𝑡 傅里叶变换形式: 𝑓(𝑡)ℎ 𝑡  𝐻 𝜇 𝐹(𝜇) 𝑓(𝑡)ℎ 𝑡  𝐻 𝜇 𝐹(𝜇) §4.2 基本概念

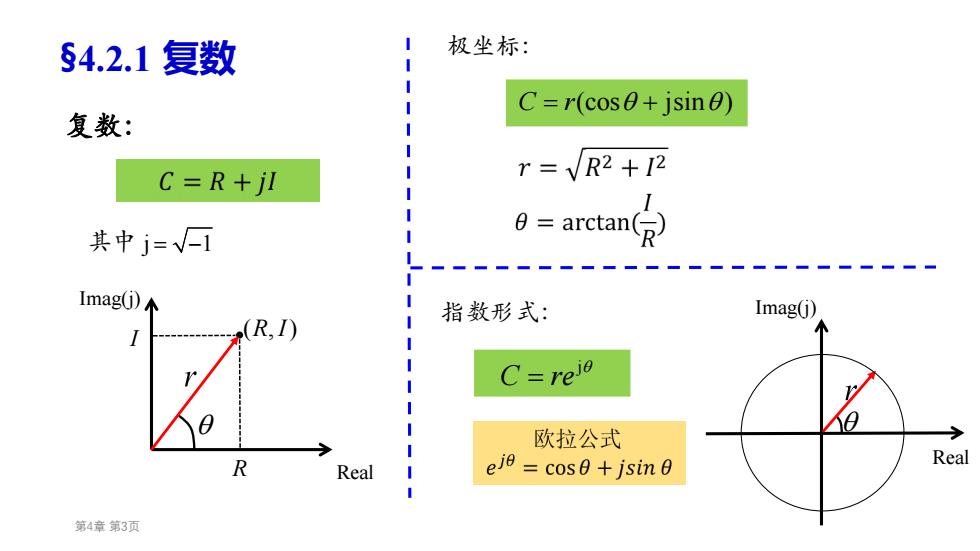
§4.2.1复数 极坐标： C=r(cosθ+jsinθ) 复数： C=R+jl r=R2+12 其中j=√ g=arctan((月 Imag( 指数形式： Imag(j) (R,) C=reio 欧拉公式 R Real Real eje=cos0+jsin 第4章第3页

第4章 第3页 复数： 极坐标： 指数形式： §4.2.1 复数 ( , ) R I Real Imag(j) R I 其中 j 1   C r   (cos jsin )   j C re   Real Imag(j) 

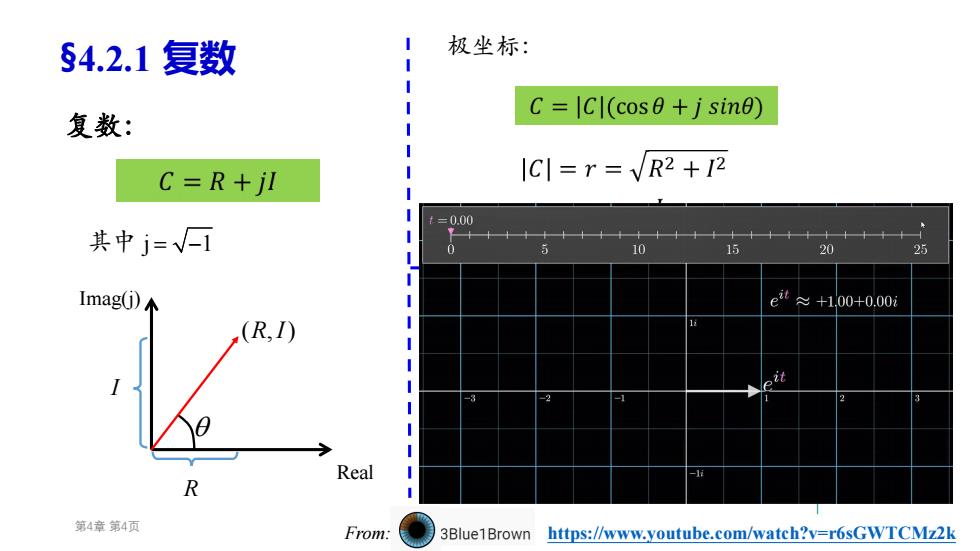
§4.2.1复数 极坐标： C=lCl(cosθ+jsin0) 复数： C=R+jl |C|=r=VR2+12 =0.00 其中j=石 0 10 公 20 25 Imag(j)个 et≈+1.00+0.00i (R,) 2 Real R 第4章第4页 From: 3Blue1Brown https://www.youtube.com/watch?v=r6sGWTCMz2k

第4章 第4页 复数： 极坐标： 指数形式： §4.2.1 复数 ( , ) R I Real Imag(j) R I 其中 j 1   From: https://www.youtube.com/watch?v=r6sGWTCMz2k

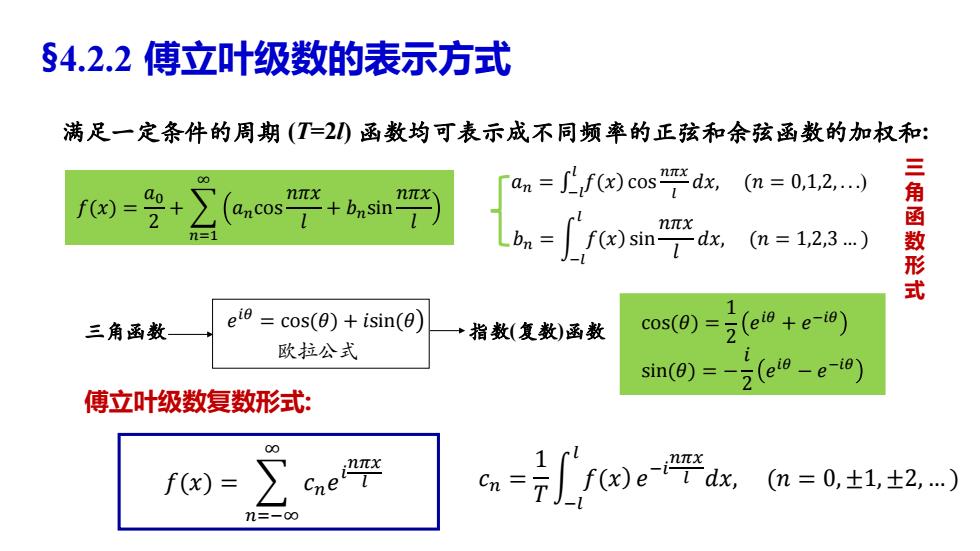
§4.2.2傅立叶级数的表示方式 满足一定条件的周期(T=2)函数均可表示成不同频率的正弦和余弦函数的加权和： an=ff(x)cos dx,(n=0.1.2...) 三 00 ao πx nπX f(x)= ancos-1 bnsin 函 77 ，(m=1,2,3.…) 数 三角函数 ei8=cos(0)+isin(0） 指数（复数）函数 欧拉公式 cos(0) sin(o)=-(ea-e0） L 傅立叶级数复数形式： 00 fa=∑cne 6n-x)dx.(n=0,士1士2) n=-o

§4.2.2 傅立叶级数的表示方式 𝑓(𝑥) = 𝑎0 2 + ෍ 𝑛=1 ∞ 𝑎𝑛cos 𝑛𝜋𝑥 𝑙 + 𝑏𝑛sin 𝑛𝜋𝑥 𝑙 ��−׬ = �𝑎� 𝑙 𝑓(𝑥) cos 𝑛𝜋𝑥 𝑙 𝑑𝑥, (𝑛 = 0,1,2, . . .) 𝑏𝑛 = න −𝑙 𝑙 𝑓(𝑥) sin 𝑛𝜋𝑥 𝑙 𝑑𝑥, (𝑛 = 1,2,3 … ) 满足一定条件的周期 (T=2l) 函数均可表示成不同频率的正弦和余弦函数的加权和: 三 角 函 数 形 式 傅立叶级数复数形式: 𝑓(𝑥) = ෍ 𝑛=−∞ ∞ 𝑐𝑛𝑒 𝑖 𝑛𝜋𝑥 𝑙 𝑐𝑛 = 1 𝑇 න −𝑙 𝑙 𝑓(𝑥) 𝑒 −𝑖 𝑛𝜋𝑥 𝑙 𝑑𝑥, (𝑛 = 0, ±1, ±2, … ) 三角函数 欧拉公式 指数(复数)函数 𝑒 ൯ 𝑖𝜃 = cos(𝜃) + 𝑖sin(𝜃 cos(𝜃) = 1 2 𝑒 𝑖𝜃 + 𝑒 −𝑖𝜃 sin(𝜃) = − 𝑖 2 𝑒 𝑖𝜃 − 𝑒 −𝑖𝜃

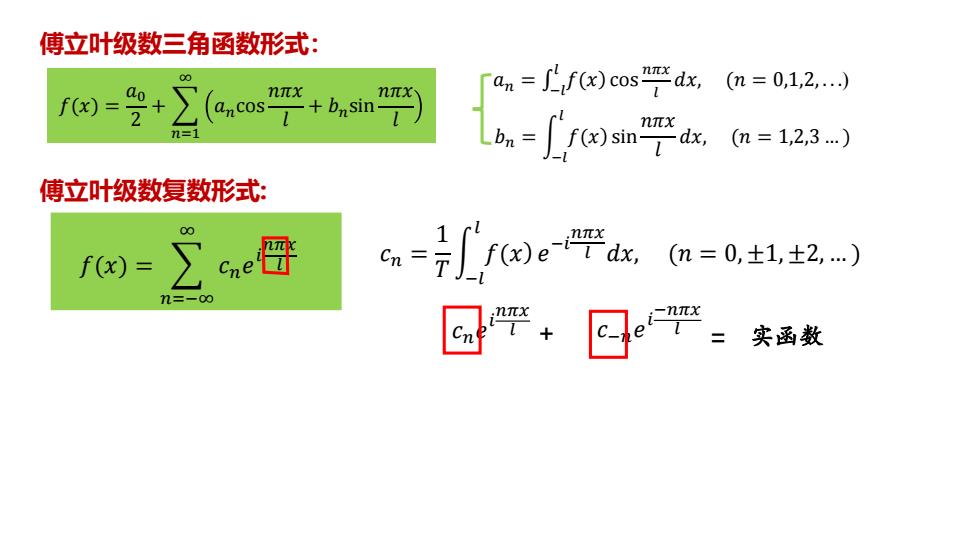
傅立叶级数三角函数形式： aeos吧+b,n (n=0,1,2,.) nπX ran=∫fx)cos"吧dk, n= (m=1,2,3…) 傅立叶级数复数形式： f)=∑ce晋 ● a=f)e学a( m=0,±1，±2，…) n=-00 回学+日学： 实函数

𝑓(𝑥) = 𝑎0 2 + ෍ 𝑛=1 ∞ 𝑎𝑛cos 𝑛𝜋𝑥 𝑙 + 𝑏𝑛sin 𝑛𝜋𝑥 𝑙 ��−׬ = �𝑎� 𝑙 𝑓(𝑥) cos 𝑛𝜋𝑥 𝑙 𝑑𝑥, (𝑛 = 0,1,2, . . .) 𝑏𝑛 = න −𝑙 𝑙 𝑓(𝑥) sin 𝑛𝜋𝑥 𝑙 𝑑𝑥, (𝑛 = 1,2,3 … ) 傅立叶级数三角函数形式： 傅立叶级数复数形式: 𝑓(𝑥) = ෍ 𝑛=−∞ ∞ 𝑐𝑛𝑒 𝑖 𝑛𝜋𝑥 𝑙 𝑐𝑛 = 1 𝑇 න −𝑙 𝑙 𝑓(𝑥) 𝑒 −𝑖 𝑛𝜋𝑥 𝑙 𝑑𝑥, (𝑛 = 0, ±1, ±2, … ) 𝑐𝑛𝑒 𝑖 𝑛𝜋𝑥 𝑙 𝑐−𝑛𝑒 𝑖 −𝑛𝜋𝑥 + 𝑙 = 实函数

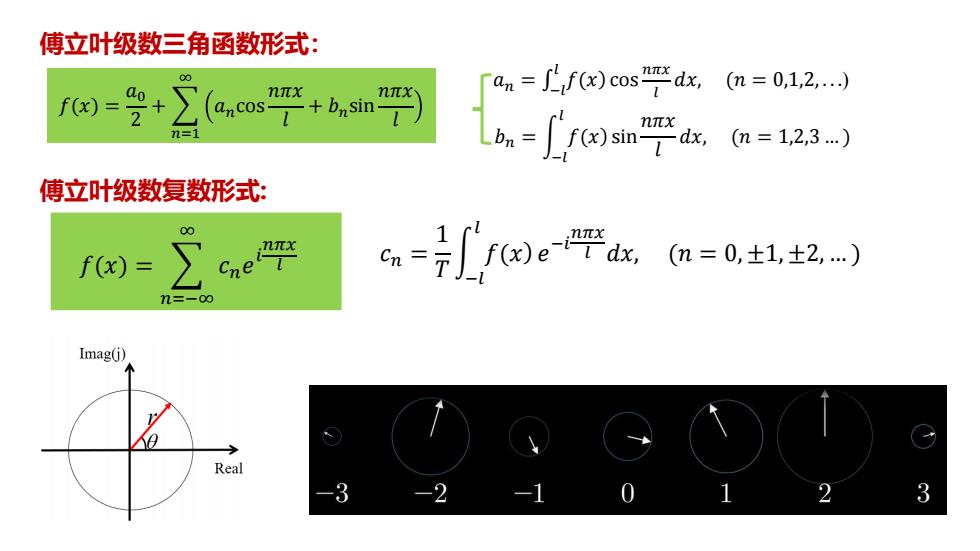
傅立叶级数三角函数形式： 00 an=∫f)cos"吧dx,m=01,2） f(x)= πx ancos-I +bnsin-I n= 6=fsn'ka=123-） 傅立叶级数复数形式： 00 f(x)= c=r网e学xa=0士，t2-） =-00 Imag(j) Real -3 -2 3

𝑓(𝑥) = 𝑎0 2 + ෍ 𝑛=1 ∞ 𝑎𝑛cos 𝑛𝜋𝑥 𝑙 + 𝑏𝑛sin 𝑛𝜋𝑥 𝑙 ��−׬ = �𝑎� 𝑙 𝑓(𝑥) cos 𝑛𝜋𝑥 𝑙 𝑑𝑥, (𝑛 = 0,1,2, . . .) 𝑏𝑛 = න −𝑙 𝑙 𝑓(𝑥) sin 𝑛𝜋𝑥 𝑙 𝑑𝑥, (𝑛 = 1,2,3 … ) 傅立叶级数三角函数形式： 傅立叶级数复数形式: 𝑓(𝑥) = ෍ 𝑛=−∞ ∞ 𝑐𝑛𝑒 𝑖 𝑛𝜋𝑥 𝑙 𝑐𝑛 = 1 𝑇 න −𝑙 𝑙 𝑓(𝑥) 𝑒 −𝑖 𝑛𝜋𝑥 𝑙 𝑑𝑥, (𝑛 = 0, ±1, ±2, … )

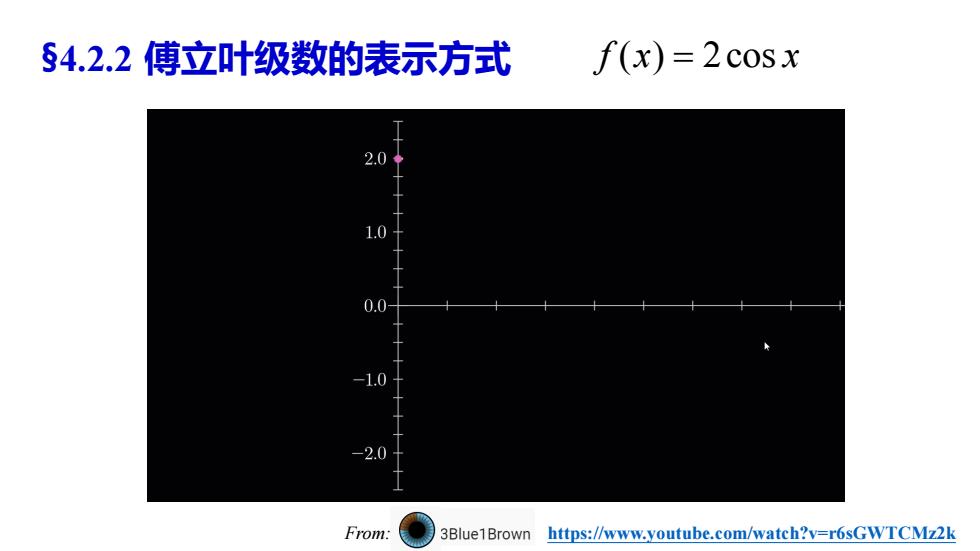
§4.2.2傅立叶级数的表示方式 f(x)=2cosx 2.0 1.0 0.0 -1.0 -2.0 From: 3Blue1Brown https://www.youtube.com/watch?v=r6sGWTCMz2k

§4.2.2 傅立叶级数的表示方式 From: https://www.youtube.com/watch?v=r6sGWTCMz2k f x x ( ) 2cos 

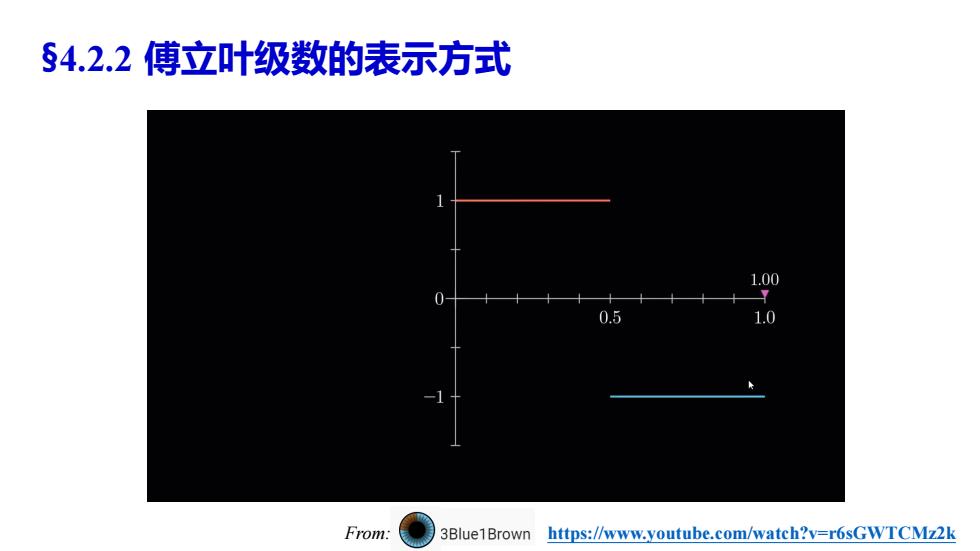
§4.2.2傅立叶级数的表示方式 1.00 0.5 From: 3Blue1Brown https://www.youtube.com/watch?v=r6sGWTCMz2k

§4.2.2 傅立叶级数的表示方式 From: https://www.youtube.com/watch?v=r6sGWTCMz2k

§4.2.2傅立叶级数的表示方式 Frequencies:-2 3 Formulas:c,e-22xit Ce-12mit -1 From: 3Blue1Brown https://www.youtube.com/watch?v=r6sGWTCMz2k

§4.2.2 傅立叶级数的表示方式 From: https://www.youtube.com/watch?v=r6sGWTCMz2k