
频率域滤波 ·4.1背景 ·4.2基本概念 ·4.3取样和取样函数的傅立叶变换 ·4.4单变量的离散傅立叶变换 ·4.5两个变量的扩展 ·4.6二维离散傅立叶变换的一些性质 ·4.7频率域滤波基础 ·4.8频率域滤波器平滑图像 ·4.9频率域滤波器锐化图像 ·4.10选择性滤波
• 4.1 背景 • 4.2 基本概念 • 4.3 取样和取样函数的傅立叶变换 • 4.4 单变量的离散傅立叶变换 • 4.5 两个变量的扩展 • 4.6 二维离散傅立叶变换的一些性质 • 4.7 频率域滤波基础 • 4.8 频率域滤波器平滑图像 • 4.9 频率域滤波器锐化图像 • 4.10 选择性滤波 频率域滤波

§4.9频域锐化滤波器 基本思想 衰减图像的傅里叶变换的高频部分可以平滑图像 ■图像中的边缘及急剧变化部分与高频分量有关,当衰减图像中的低频分量时会相对地强调其高 频分量,从而加强图像中边缘及急刷变化部分,达到图像锐化目的。 基本方法 高通滤波器=1-低通滤波器 Hhp(u,v)=1-Hip(u,v)
衰减图像的傅里叶变换的高频部分可以平滑图像 基本方法 高 通 滤 波 器 = 1 − 低 通 滤 波 器 §4.9 频域锐化滤波器 基本思想 图像中的边缘及急剧变化部分与高频分量有关,当衰减图像中的低频分量时会相对地强调其高 频分量,从而加强图像中边缘及急剧变化部分,达到图像锐化目的。 𝐻ℎ𝑝(𝑢, 𝑣) = 1 − 𝐻𝑙𝑝(𝑢, 𝑣൯
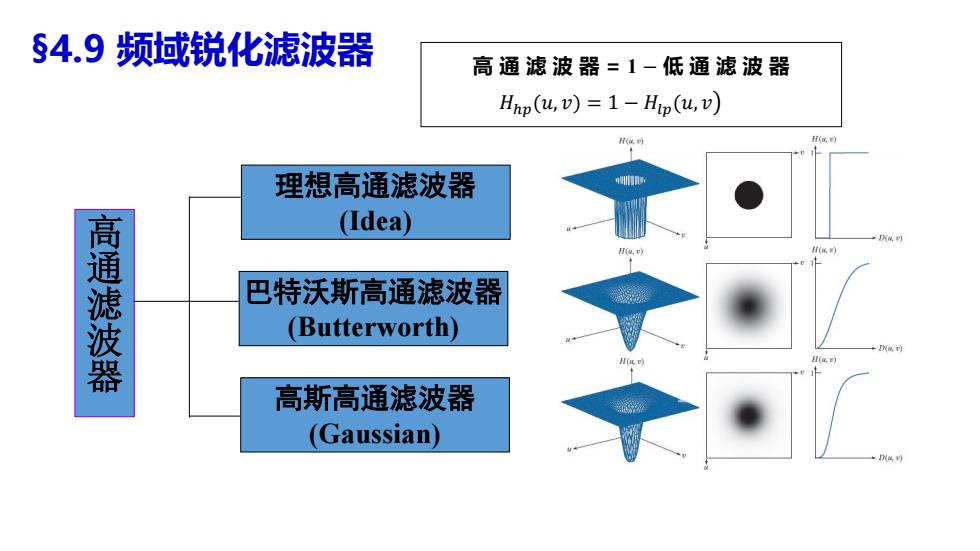
§4.9频域锐化滤波器 高通滤波器=1一低通滤波器 Hnp(u,v)=1-Hip(u,v) H低着 理想高通滤波器 (Idea) 高通滤波器 、 H(属 巴特沃斯高通滤波器 (Butterworth) 高斯高通滤波器 (Gaussian)
§4.9 频域锐化滤波器 理想高通滤波器 (Idea) 巴特沃斯高通滤波器 (Butterworth) 高斯高通滤波器 (Gaussian) 高 通 滤 波 器 高 通 滤 波 器 = 1 − 低 通 滤 波 器 𝐻ℎ𝑝(𝑢, 𝑣) = 1 − 𝐻𝑙𝑝(𝑢, 𝑣൯

§4.9频域锐化滤波器 理想高通滤波器 巴特沃斯高通滤波器 高斯高通滤波器 空域表示形式
理想高通滤波器 巴特沃斯高通滤波器 高斯高通滤波器 §4.9 频域锐化滤波器 空 域 表 示 形 式
§4.9.1理想高通滤波器HPF 理想高通滤波器 理想高通滤波器H(,)可给出如下形式: Hnp(u,v) ifD(u,v)≤Do if D(u,v)>Do D(u,) e-6- 低通lowpass Hn(u,D))= 10 ifD(u,)≤Do if D(u,v)>Do IHPF同LPF是相对的, Hhp(u,v)=1-Hp(u,v) IHPF通过将半径为Do的圆 息 内的所有频率置零,而毫无 衰减地通过圆外的所有频率。 高通highpass ifD(,)≤Do if D(u,v)>Do
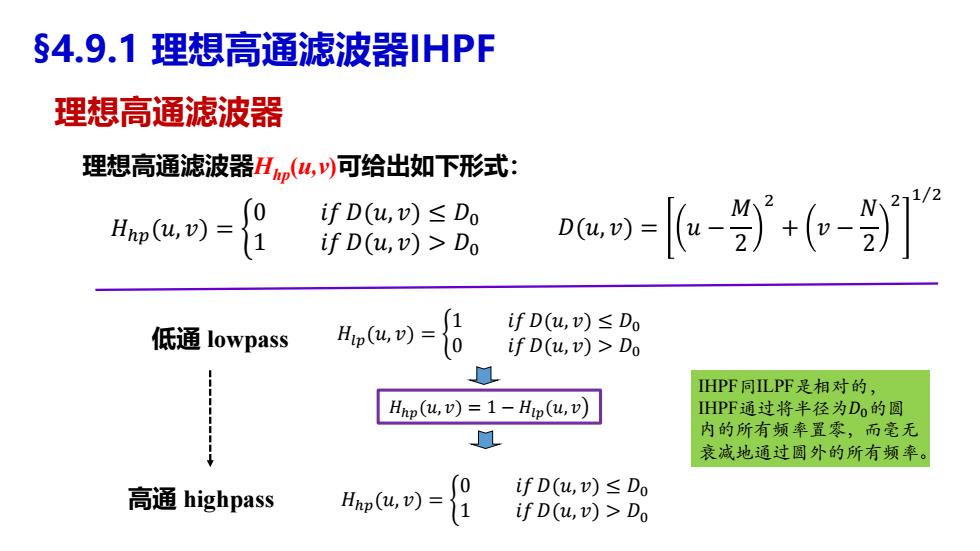
理想高通滤波器Hhp(u,v)可给出如下形式: 低通 lowpass 高通 highpass IHPF同ILPF是相对的, IHPF通过将半径为𝐷0的圆 内的所有频率置零,而毫无 衰减地通过圆外的所有频率。 §4.9.1 理想高通滤波器IHPF 理想高通滤波器 𝐻ℎ𝑝(𝑢, 𝑣) = ቊ 0 𝑖𝑓𝐷(𝑢, 𝑣) ≤ 𝐷0 1 𝑖𝑓𝐷(𝑢, 𝑣) > 𝐷0 𝐷(𝑢, 𝑣) = 𝑢 − 𝑀 2 2 + 𝑣 − 𝑁 2 2 1Τ2 𝐻𝑙𝑝(𝑢, 𝑣) = ቊ 1 𝑖𝑓𝐷(𝑢, 𝑣) ≤ 𝐷0 0 𝑖𝑓𝐷(𝑢, 𝑣) > 𝐷0 𝐻ℎ𝑝(𝑢, 𝑣) = 1 − 𝐻𝑙𝑝(𝑢, 𝑣൯ 𝐻ℎ𝑝(𝑢, 𝑣) = ቊ 0 𝑖𝑓𝐷(𝑢, 𝑣) ≤ 𝐷0 1 𝑖𝑓𝐷(𝑢, 𝑣) > 𝐷0
§4.9.1理想高通滤波器HPF Hnp(u,v)= 0 ifD(u,)≤Do if D(u,v)>Do 理想高通滤波器的不同表征形式 Hnp(,v)=1-Hp(u,v) Frequency domain Spatial domain H(,) H(4 振铃效应 ILPF D( Frequency domain Spatial domain H(u.v) H(u,v) 10 锐化作用 IHPF 振 -D(M.v 理想高通有振铃效应吗?
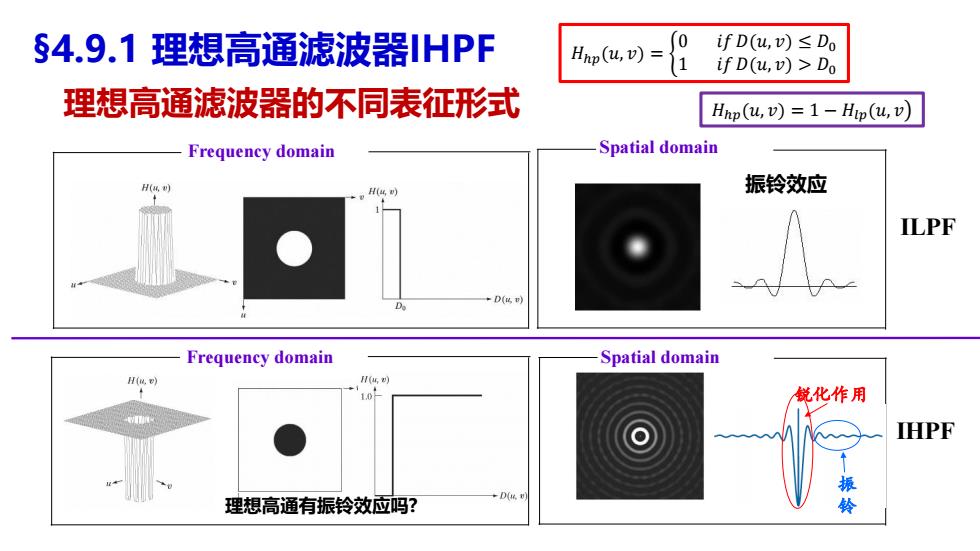
振铃效应 Frequency domain Spatial domain §4.9.1 理想高通滤波器IHPF 理想高通滤波器的不同表征形式 𝐻ℎ𝑝(𝑢, 𝑣) = ቊ 0 𝑖𝑓𝐷(𝑢, 𝑣) ≤ 𝐷0 1 𝑖𝑓𝐷(𝑢, 𝑣) > 𝐷0 ILPF Frequency domain 理想高通有振铃效应吗? Spatial domain IHPF 𝐻ℎ𝑝(𝑢, 𝑣) = 1 − 𝐻𝑙𝑝(𝑢, 𝑣൯ 锐化作用 振 铃
§4.9.1理想高通滤波器HPF Example of ideal highpass filters 锐化作用 Da越小,振铃 效果越明显 理想目标是:平坦区域全部变 振 为黑色,变化部分变为白色 g回回回 a ⊙⊙⊙ aaaaaaaa aaa aaaa 8@@@恩 高盟丝么瓶烈圈 Input image D。=30 D,=60 D=160
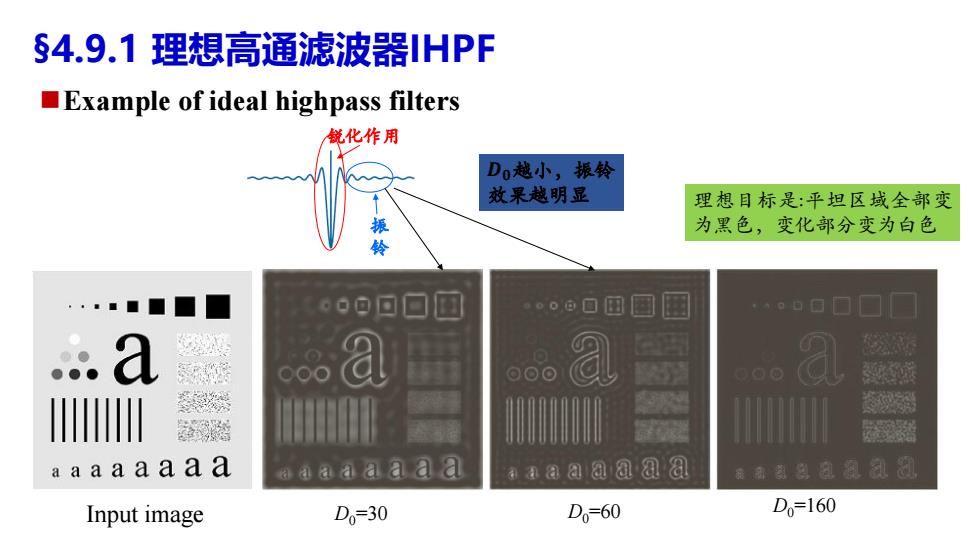
Input image D0=30 D0=60 D0=160 理想目标是:平坦区域全部变 为黑色,变化部分变为白色 𝑫𝟎越小,振铃 效果越明显 §4.9.1 理想高通滤波器IHPF Example of ideal highpass filters 锐化作用 振 铃

§4.9.2巴特沃斯高通滤波器BHPF Transfer function of Butterworth lowpass filters: 1 Hu,)=1+D(u,v)/Do2n Hnp(u,v)=1-Hip(u,v) Transfer function of Butterworth highpass 截止频率为D的n阶巴特沃斯高通滤波器(BHPF),其传递函数H(,v)为 H(u,)= 1+[Do/D(u,)]2m u0=e-7+e-T
Transfer function of Butterworth lowpass filters: §4.9.2 巴特沃斯高通滤波器BHPF Transfer function of Butterworth highpass 截止频率为D0的n阶巴特沃斯高通滤波器(BHPF),其传递函数H(u,v)为 𝐻(𝑢, 𝑣) = 1 1 + 𝐷 Τ ) 0 𝐷 (𝑢, 𝑣 2𝑛 𝐷(𝑢, 𝑣) = 𝑢 − 𝑀 2 2 + 𝑣 − 𝑁 2 2 1Τ2 𝐻ℎ𝑝(𝑢, 𝑣) = 1 − 𝐻𝑙𝑝(𝑢, 𝑣൯ 𝐻(𝑢, 𝑣) = 1 1 + 𝐷(𝑢, 𝑣 )Τ𝐷0 2𝑛
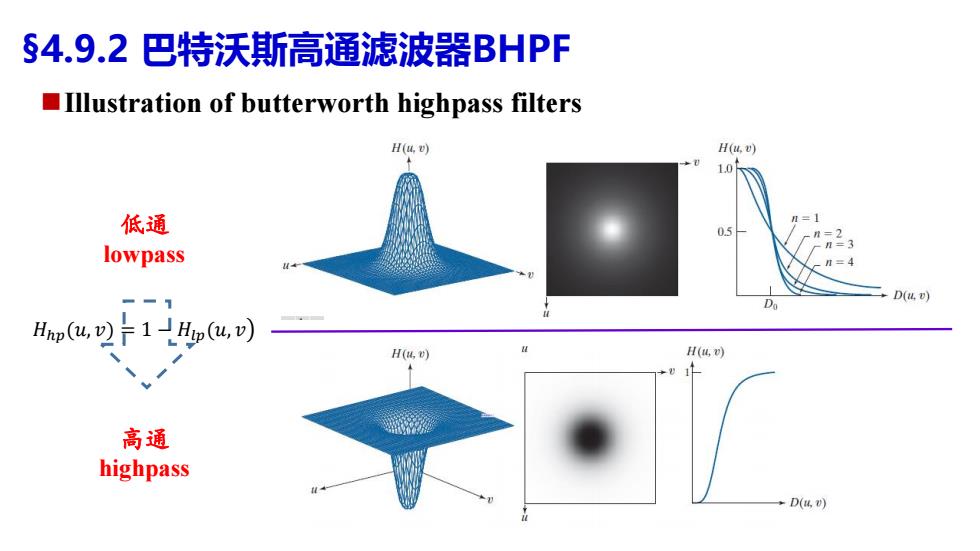
§4.9.2巴特沃斯高通滤波器BHPF Illustration of butterworth highpass filters H() H(u.v) 1.0 低通 lowpass -D(u. Do Hnp(u,v)1Hip(u,v) H(,) H(0) 高通 highpass +D(4)
Illustration of butterworth highpass filters 高通 highpass 低通 lowpass §4.9.2 巴特沃斯高通滤波器BHPF 𝐻ℎ𝑝(𝑢, 𝑣) = 1 − 𝐻𝑙𝑝(𝑢, 𝑣൯
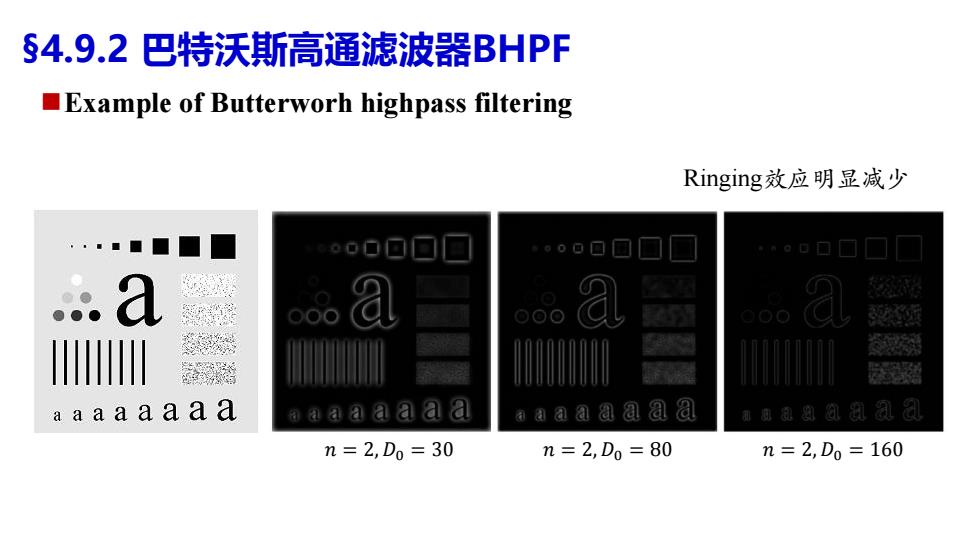
§4.9.2巴特沃斯高通滤波器BHPF Example of Butterworh highpass filtering Ringing效应明显减少 a aaaaaaa aaaa aaa a 用团a图团周周 和息数红凯风剑 n=2,Do=30 n=2,D0=80 n=2,D0=160
Ringing效应明显减少 𝑛 = 2,𝐷0 = 30 𝑛 = 2,𝐷0 = 80 𝑛 = 2,𝐷0 = 160 §4.9.2 巴特沃斯高通滤波器BHPF Example of Butterworh highpass filtering