
频率域滤波 ·4.1背景 ·4.2基本概念 ·4.3取样和取样函数的傅立叶变换 ·4.4单变量的离散傅立叶变换 ·4.5两个变量的扩展 ·4.6二维离散傅立叶变换的一些性质 ·4.7频率域滤波基础 ·4.8频率域滤波器平滑图像 ·4.9频率域滤波器锐化图像 ·4.10选择性滤波
• 4.1 背景 • 4.2 基本概念 • 4.3 取样和取样函数的傅立叶变换 • 4.4 单变量的离散傅立叶变换 • 4.5 两个变量的扩展 • 4.6 二维离散傅立叶变换的一些性质 • 4.7 频率域滤波基础 • 4.8 频率域滤波器平滑图像 • 4.9 频率域滤波器锐化图像 • 4.10 选择性滤波 频率域滤波

§4.6二维离散傅立叶变换的性质 。空间和频率间隔的关系 假定对连续函数f(t,z)取样生成了一幅数字图像f(x,y),它由分别在t和z方 向所取的M*N个样点组成。令△T和△Z表示样本间的间隔,则相应离散频率 域变量间的间隔分别由 1 1 △u= M△T 频 2u=M△u= △T 整个 1 分 1 △v= N△Z 率 2v=N△v= △Z 频率范围 频率域样本间的间隔与空间样本间的间距和样本数成反比
频率域样本间的间隔与空间样本间的间距和样本数成反比。 §4.6 二维离散傅立叶变换的性质 空间和频率间隔的关系 假定对连续函数𝑓(𝑡, 𝑧)取样生成了一幅数字图像𝑓(𝑥, 𝑦),它由分别在𝑡和𝑧方 向所取的𝑀 ∗ 𝑁个样点组成。令∆𝑇和∆𝑍表示样本间的间隔,则相应离散频率 域变量间的间隔分别由 ∆𝑢 = 1 𝑀∆𝑇 ∆𝑣 = 1 𝑁∆𝑍 Ω𝑢 = 𝑀 △ 𝑢 = 1 △ 𝑇 Ω𝑣 = 𝑁 △ 𝑣 = 1 △ 𝑍 整 个 频 率 范 围 频 率 分 辨 率
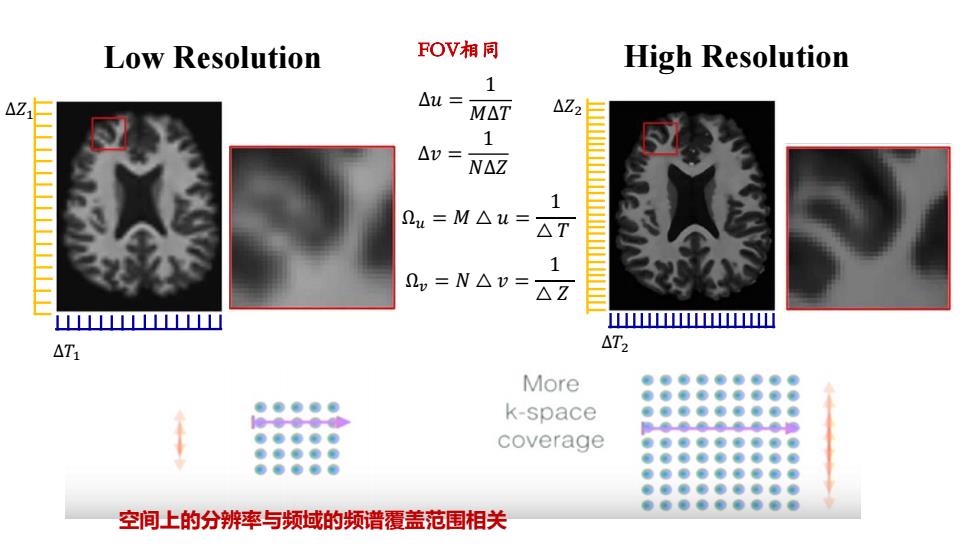
Low Resolution FOV相同 High Resolution 1 △Z1 △u= M△T △Z2 1 △0= N△Z 1 2u=M△u= △T 1 2v=N△v= △Z LLLLLLLLLLLLLLL ATi △T2 More k-space coverage 空间上的分辨率与频域的频谱覆盖范围相关
Low Resolution High Resolution FOV相同 ∆𝑢 = 1 𝑀∆𝑇 ∆𝑣 = 1 𝑁∆𝑍 Ω𝑢 = 𝑀 △ 𝑢 = 1 △ 𝑇 Ω𝑣 = 𝑁 △ 𝑣 = 1 △ 𝑍 ∆𝑇1 ∆𝑍1 ∆𝑇2 ∆𝑍2 空间上的分辨率与频域的频谱覆盖范围相关
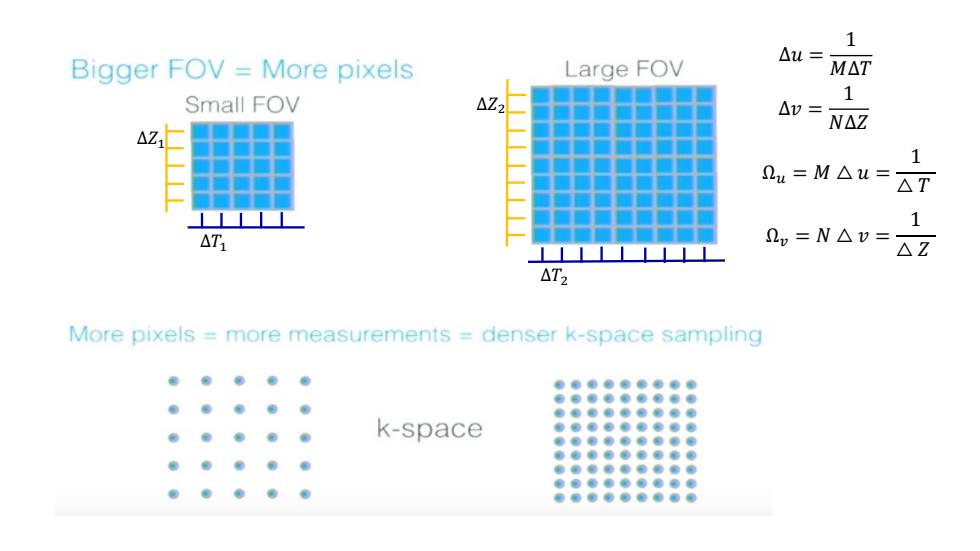
1 △u= Bigger FOV More pixels Large FOV M△T Small FOV △Z2 1 △V= N△Z △Z 1 2u=M△u= △T 1 △T1 2m=N△v= △Z △T2 More pixels more measurements denser k-space sampling k-space
∆ 𝑢 = 1 𝑀 ∆ 𝑇 ∆ 𝑣 = 1 𝑁 ∆ 𝑍 Ω 𝑢 = 𝑀 △ 𝑢 = 1△ 𝑇 Ω 𝑣 = 𝑁 △ 𝑣 = 1△ 𝑍 ∆ 𝑇1 ∆ 𝑍 1 ∆ 𝑇2 ∆ 𝑍 2

§4.6二维离散傅立叶变换的性质 。平移和旋转 fx,y)e7+)→Fu-o,v-o) f(x-xo.y-yo)F(u,v)e-j2n() f(r,日+B0)台F(p,p+o)若f(x,y)旋转0o角度,则F(u,v)也旋转相同的角度。 ● 平均值 M-1N-1 M-1N-1 MN·f(x,y) X=0y=0 |F(0,0)川是谱的最大分量
若𝑓(𝑥, 𝑦)旋转𝜃0角度,则𝐹 𝑢, 𝑣 也旋转相同的角度。 𝑭(𝟎, 𝟎) 是谱的最大分量 §4.6 二维离散傅立叶变换的性质 平移和旋转 𝑓 𝑥, 𝑦 𝑒 𝑗2𝜋 𝑢0𝑥 𝑀 + 𝑣0𝑦 𝑁 ⟺ 𝐹(𝑢 − 𝑢0, 𝑣 − 𝑣0) 𝑓(𝑥 − 𝑥0, 𝑦 − 𝑦0) ⟺ 𝐹(𝑢, 𝑣)𝑒 −𝑗2𝜋 𝑥0𝑢 𝑀 + 𝑦0𝑣 𝑁 𝑓 𝑟, 𝜃 + 𝜃0 ⟺ 𝐹(𝜌,𝜑 + 𝜃0) 平均值 𝐹 0,0 = 𝑀𝑁 ∙ 1 𝑀𝑁 𝑥=0 𝑀−1 𝑦=0 𝑁−1 𝑓 𝑥, 𝑦 𝑒 −𝑗2𝜋 0∗𝑢 𝑀 + 0∗𝑣 𝑁 = 𝑀𝑁 ∙ 1 𝑀𝑁 𝑥=0 𝑀−1 𝑦=0 𝑁−1 𝑓 𝑥, 𝑦 = 𝑀𝑁 ∙ 𝑓ҧ(𝑥, 𝑦)

§4.6二维离散傅立叶变换的性质 ,周期性 离散的二维傅里叶变换及其反变换在u方向和)方向是无限周期的 F(u,v)=F(u+kM,v+k2N) f(x,y)=f(x+kiM,y+k2N) 其中k1,k2是整数 周期性在基于DFT算法的实现上有着重要作用
§4.6 二维离散傅立叶变换的性质 周期性 离散的二维傅里叶变换及其反变换在𝑢方向和𝑣方向是无限周期的 𝐹 𝑢, 𝑣 = 𝐹 𝑢 + 𝑘1𝑀, 𝑣 + 𝑘2𝑁 𝑓 𝑥, 𝑦 = 𝑓(𝑥 + 𝑘1𝑀, 𝑦 + 𝑘2𝑁) 其中 𝑘1, 𝑘2是整数 周期性在基于DFT算法的实现上有着重要作用
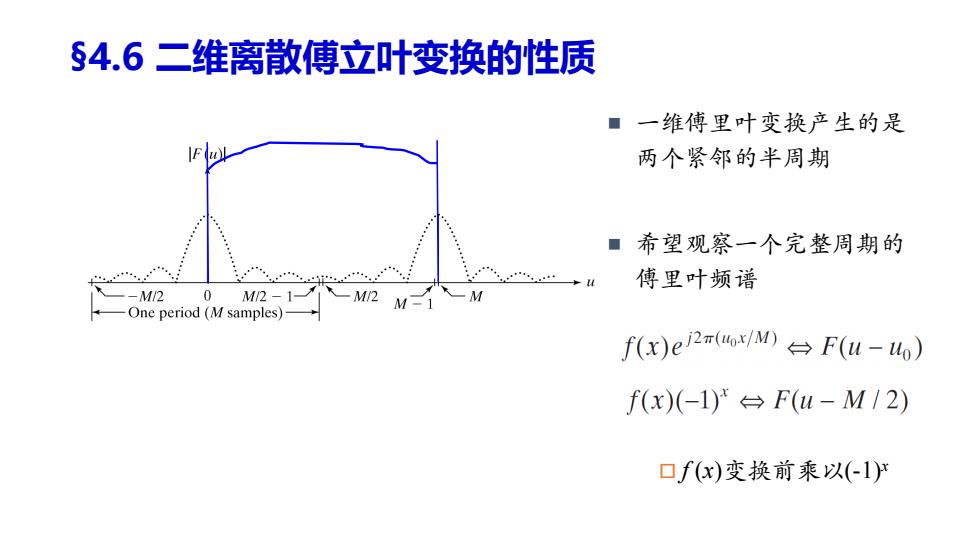
§4.6二维离散傅立叶变换的性质 ■一维傅里叶变换产生的是 u 两个紧邻的半周期 ■希望观察一个完整周期的 傅里叶频谱 --M2 0 M/2-1- -M2 One period(M samples)- f(x)e2mM)台F(u-o) f(x)(-1)'台F(u-M/2) 口f(x)变换前乘以(1)H
希望观察一个完整周期的 傅里叶频谱 §4.6 二维离散傅立叶变换的性质 一维傅里叶变换产生的是 两个紧邻的半周期 f (x)变换前乘以(-1)x
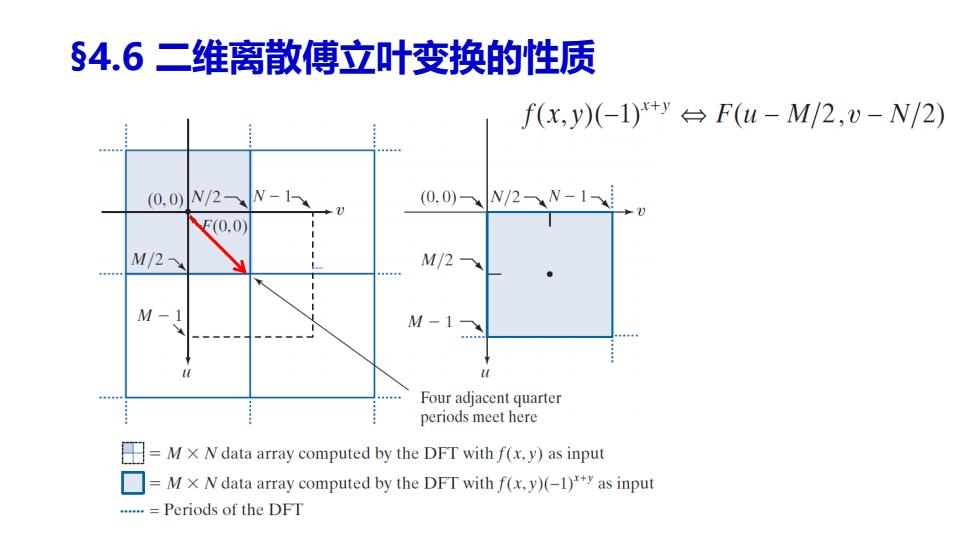
§4.6二维离散傅立叶变换的性质 f(x,y)(-1)+y台F(u-M/2,v-N/2) (0,0)N/2N-1 (0.0)N/2N-1 E(0.0) M/2¥ M/2 M M-1 Four adjacent quarter periods meet here =MX N data array computed by the DFT with f(x.y)as input =MX N data array computed by the DFT with f(x.y)(-1)y as input …=Periods of the DFT
§4.6 二维离散傅立叶变换的性质

§4.6二维离散傅立叶变换的性质 ·傅里叶谱和相角 极坐标下,二维DFT可表示为 F(u,v)=F(u,v)leip(uv) 幅度,也称为傅里叶谱或频谱 IF(u,v)l=[R2(u,v)+I2(u,v)]1/2 频谱,信息大小 相角 p(u,v)arctan I(u,) R(u,】 相角,定位信息
极坐标下,二维DFT可表示为 𝐹 𝑢, 𝑣 = 𝐹(𝑢, 𝑣) 𝑒 𝑗𝜑(𝑢,𝑣) 幅度,也称为傅里叶谱或频谱 𝐹(𝑢, 𝑣) = 𝑅 2 𝑢, 𝑣 + 𝐼 2 (𝑢, 𝑣) 1/2 𝜑 𝑢, 𝑣 = 𝑎𝑟𝑐𝑡𝑎𝑛 𝐼(𝑢, 𝑣) 𝑅(𝑢, 𝑣) 相角 §4.6 二维离散傅立叶变换的性质 傅里叶谱和相角 频谱,信息大小 相角,定位信息

§4.6二维离散傅立叶变换的性质 原点在左上角,所 以变换的原点区域 包含了最高值 周期性中心化该 D(u,v)= 谱,变换前原图 像乘以(-1)x+y ■og(1+lF(u,v)D
原点在左上角,所 以变换的原点区域 包含了最高值 周期性中心化该 谱,变换前原图 像乘以(−1) 𝑥+𝑦 §4.6 二维离散傅立叶变换的性质 𝐷 𝑢, 𝑣 = 𝑙𝑜𝑔(1 + 𝐹 𝑢, 𝑣 )