
频率域滤波 ·4.1背景 ·4.2基本概念 ·4.3取样和取样函数的傅立叶变换 ·4.4单变量的离散傅立叶变换 ·4.5两个变量的扩展 ·4.6二维离散傅立叶变换的一些性质 ·4.7频率域滤波基础 ·4.8频率域滤波器平滑图像 ·4.9频率域滤波器锐化图像 ·4.10选择性滤波
• 4.1 背景 • 4.2 基本概念 • 4.3 取样和取样函数的傅立叶变换 • 4.4 单变量的离散傅立叶变换 • 4.5 两个变量的扩展 • 4.6 二维离散傅立叶变换的一些性质 • 4.7 频率域滤波基础 • 4.8 频率域滤波器平滑图像 • 4.9 频率域滤波器锐化图像 • 4.10 选择性滤波 频率域滤波
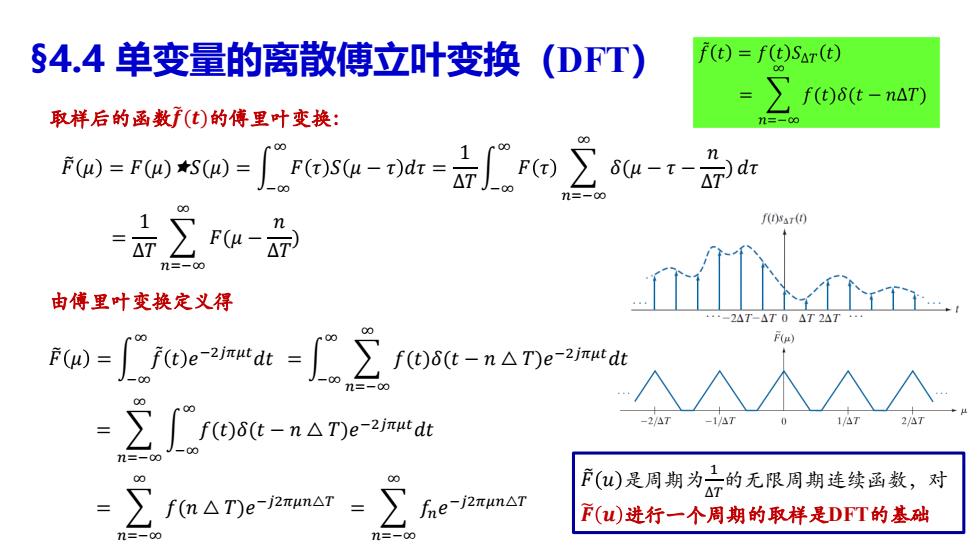
§4.4单变量的离散傅立叶变换(DFT) f(t)=f(t)SAT(t) =∑fost-nan) 取样后的函数f(t)的傅里叶变换: FW=r*s0W=resu-odr=Cro∑80u-i-沿dr f(ssr() 由傅里叶变换定义得 0△T2△ POD()e-md-T -2/△7 -17 2/A7 ∑a T)e-ptr- F()是周期为行的无限周期连续函数,对 fne-fj2un△T F()进行一个周期的取样是DFT的基础
§4.4 单变量的离散傅立叶变换(DFT) 取样后的函数𝒇෨(𝒕)的傅里叶变换: 由傅里叶变换定义得 𝐹෨ 𝜇 = න −∞ ∞ 𝑓ሚ 𝑡 𝑒 −2𝑗𝜋𝜇𝑡𝑑𝑡 𝐹෨ 𝑢 是周期为 1 ∆𝑇 的无限周期连续函数,对 𝑭෩ 𝒖 进行一个周期的取样是DFT的基础 𝐹෨ 𝜇 = 𝐹(𝜇)𝑆(𝜇) = න −∞ ∞ 𝐹 𝜏 𝑆 𝜇 − 𝜏 𝑑𝜏 = 1 ∆𝑇 න −∞ ∞ 𝐹 𝜏 𝑛=−∞ ∞ 𝛿(𝜇 − 𝜏 − 𝑛 ∆𝑇 ) 𝑑𝜏 = 1 ∆𝑇 𝑛=−∞ ∞ 𝐹(𝜇 − 𝑛 ∆𝑇 ) = න −∞ ∞ 𝑛=−∞ ∞ 𝑓(𝑡)𝛿(𝑡 − 𝑛 △ 𝑇)𝑒 −2𝑗𝜋𝜇𝑡𝑑𝑡 = 𝑛=−∞ ∞ 𝑓(𝑛 △ 𝑇)𝑒 −𝑗2𝜋𝜇𝑛△𝑇 = 𝑛=−∞ ∞ න −∞ ∞ 𝑓(𝑡)𝛿(𝑡 − 𝑛 △ 𝑇)𝑒 −2𝑗𝜋𝜇𝑡𝑑𝑡 = 𝑛=−∞ ∞ 𝑓𝑛𝑒 −𝑗2𝜋𝜇𝑛△𝑇
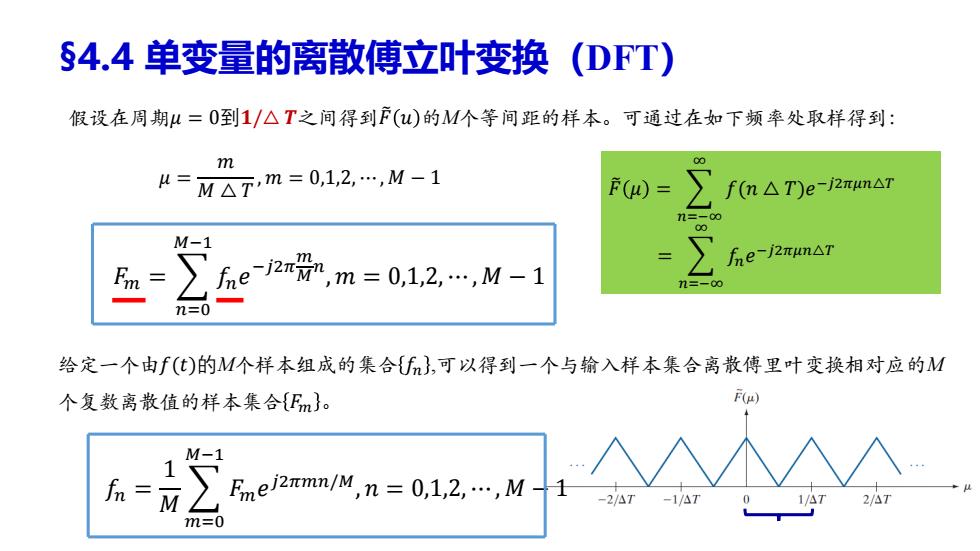
S4.4单变量的离散傅立叶变换(DFT) 假设在周期u=0到1/△T之间得到F()的M个等间距的样本。可通过在如下频率处取样得到: m k=M△T,m=0,12,,M-1 ()= f(n△T)e-j2mm△T n=-00 00 M-1 e27,m=0,12,,M-1 fne-j2run△T n=-00 n=0 给定一个由f(t)的M个样本组成的集合Uf},可以得到一个与输入样本集合离散傅里叶变换相对应的M 个复数离散值的样本集合{Em}。 F(4) M-1 fn=M Fme jznmn/M,n=0,1,2....M- -2/A7 -1/△1 2/△7 m=0
假设在周期𝜇 = 0到𝟏/△ 𝑻之间得到𝐹෨ 𝑢 的M个等间距的样本。可通过在如下频率处取样得到: 𝜇 = 𝑚 𝑀 △ 𝑇 , 𝑚 = 0,1,2, ⋯ , 𝑀 − 1 𝐹𝑚 = 𝑛=0 𝑀−1 𝑓𝑛𝑒 −𝑗2𝜋 𝑚 𝑀 𝑛 , 𝑚 = 0,1,2, ⋯ , 𝑀 − 1 给定一个由𝑓(𝑡)的M个样本组成的集合 𝑓𝑛 ,可以得到一个与输入样本集合离散傅里叶变换相对应的M 个复数离散值的样本集合 𝐹𝑚 。 𝐹෨ 𝜇 = 𝑛=−∞ ∞ 𝑓(𝑛 △ 𝑇)𝑒 −𝑗2𝜋𝜇𝑛△𝑇 = 𝑛=−∞ ∞ 𝑓𝑛𝑒 −𝑗2𝜋𝜇𝑛△𝑇 §4.4 单变量的离散傅立叶变换(DFT) 𝑓𝑛 = 1 𝑀 𝑚=0 𝑀−1 𝐹𝑚𝑒 𝑗2𝜋𝑚𝑛/𝑀 , 𝑛 = 0,1,2, ⋯ , 𝑀 − 1

§4.4单变量的离散傅立叶变换(DFT) 离散傅里叶变换(DFT)适用于任何均匀取样的有限离散样本集。 离散傅里叶变换(DFT) M-1 Fm= he7,m=0,12,,M-1 Eo-ag=a42-M- x=0 离散傅里叶变换(DFT,inverse discrete fourier transform) M-1 A 1 fn二M Fnej2nmn/M,n =0,1,2,..M-1 F(0e2mux/W,x=0,12,…,M-1 m=0 2u=0 具有周期性 F(u)=F(u+kM) f(x)=f(x+kM)
离散傅里叶变换(DFT)适用于任何均匀取样的有限离散样本集。 𝐹 𝑢 = 𝑥=0 𝑀−1 𝑓(𝑥)𝑒 −𝑗2𝜋𝑢𝑥/𝑀 , 𝑢 = 0,1,2, ⋯ , 𝑀 − 1 𝑓 𝑥 = 1 𝑀 𝑢=0 𝑀−1 𝐹(𝑢)𝑒 𝑗2𝜋𝑢𝑥/𝑀 , 𝑥 = 0,1,2, ⋯ , 𝑀 − 1 §4.4 单变量的离散傅立叶变换(DFT) 𝐹𝑚 = 𝑛=0 𝑀−1 𝑓𝑛𝑒 −𝑗2𝜋 𝑚 𝑀 𝑛 , 𝑚 = 0,1,2, ⋯ , 𝑀 − 1 𝑓𝑛 = 1 𝑀 𝑚=0 𝑀−1 𝐹𝑚𝑒 𝑗2𝜋𝑚𝑛/𝑀 , 𝑛 = 0,1,2, ⋯ , 𝑀 − 1 离散傅里叶变换 (DFT) 离散傅里叶变换 (IDFT, inverse discrete fourier transform) 具有周期性 𝐹 𝑢 = 𝐹 𝑢 + 𝑘𝑀 𝑓 𝑥 = 𝑓 𝑥 + 𝑘𝑀
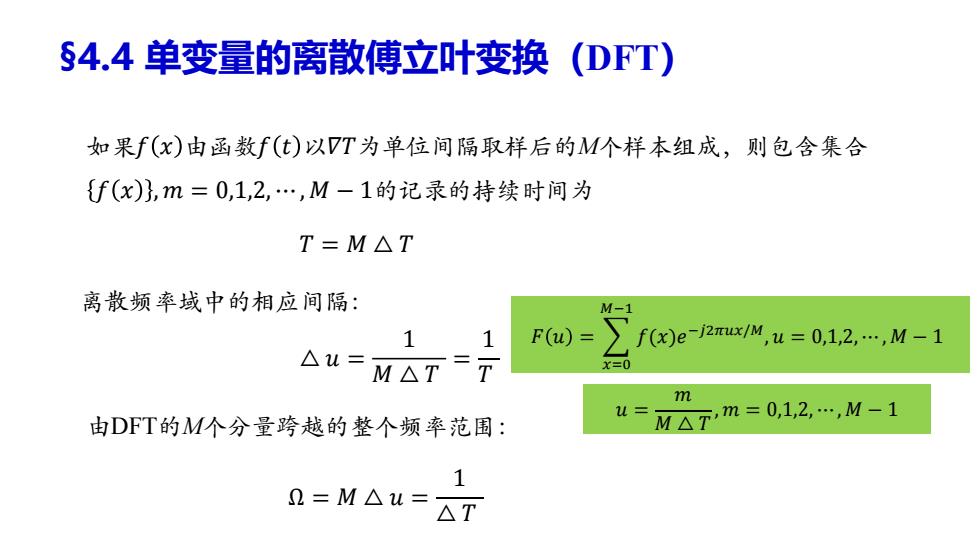
S4.4单变量的离散傅立叶变换(DFT) 如果f(x)由函数f(t)以7T为单位间隔取样后的M个样本组成,则包含集合 {f(x)},m=0,1,2,…,M-1的记录的持续时间为 T=M△T 离散频率域中的相应间隔: M-1 1 1 F(u)= f(x)eJ2mx/M,u=0,1,2,…,M-1 △u=M△T=T X=0 m 由DFT的M个分量跨越的整个频率范围: u=M△Tm=0,12,…,M-1 1 2=M△u= △T
§4.4 单变量的离散傅立叶变换(DFT) 如果𝑓 𝑥 由函数𝑓 𝑡 以𝛻𝑇为单位间隔取样后的M个样本组成,则包含集合 𝑓 𝑥 , 𝑚 = 0,1,2, ⋯ , 𝑀 − 1的记录的持续时间为 𝑇 = 𝑀 △ 𝑇 △ 𝑢 = 1 𝑀 △ 𝑇 = 1 𝑇 Ω = 𝑀 △ 𝑢 = 1 △ 𝑇 离散频率域中的相应间隔: 由DFT的M个分量跨越的整个频率范围: 𝐹 𝑢 = 𝑥=0 𝑀−1 𝑓(𝑥)𝑒 −𝑗2𝜋𝑢𝑥/𝑀 , 𝑢 = 0,1,2, ⋯ , 𝑀 − 1 𝑢 = 𝑚 𝑀 △ 𝑇 , 𝑚 = 0,1,2, ⋯ , 𝑀 − 1

频率域滤波 ·4.1背景 ·4.2基本概念 ·4.3取样和取样函数的傅立叶变换 ·4.4单变量的离散傅立叶变换 ·4.5两个变量的扩展 ·4.6二维离散傅立叶变换的一些性质 ·4.7频率域滤波基础 ·4.8频率域滤波器平滑图像 ·4.9频率域滤波器锐化图像 ·4.10选择性滤波
• 4.1 背景 • 4.2 基本概念 • 4.3 取样和取样函数的傅立叶变换 • 4.4 单变量的离散傅立叶变换 • 4.5 两个变量的扩展 • 4.6 二维离散傅立叶变换的一些性质 • 4.7 频率域滤波基础 • 4.8 频率域滤波器平滑图像 • 4.9 频率域滤波器锐化图像 • 4.10 选择性滤波 频率域滤波

§4.5两个变量的离散傅里叶变换 ,二维冲激及其取样特性一连续变量 两个连续变量1和z的冲激定义为 00 00, t=z=0 6(t,z)= 10, 8(t,z)dtdz =1 other -00 00 二维冲激在积分下也有一维情况下的取样特性 f(t,z)5(t,z)dtdz=f(0,0) 更一般地,位于坐标(to,Zo)处的冲激 CCfea5it-aa-%wdtd虹=fcu
二维冲激在积分下也有一维情况下的取样特性 න −∞ ∞ න −∞ ∞ 𝑓(𝑡, 𝑧)𝛿 𝑡, 𝑧 𝑑𝑡𝑑𝑧 = 𝑓(0,0) 更一般地,位于坐标 𝑡0, 𝑧0 处的冲激 න −∞ ∞ න −∞ ∞ 𝑓(𝑡, 𝑧)𝛿 𝑡 − 𝑡0, 𝑧 − 𝑧0 𝑑𝑡𝑑𝑧 = 𝑓(𝑡0, 𝑧0) 二维冲激及其取样特性—连续变量 𝛿 𝑡, 𝑧 = ቊ ∞, 𝑡 = 𝑧 = 0 0, 𝑜𝑡ℎ𝑒𝑟 න −∞ ∞ න −∞ ∞ 𝛿 𝑡, 𝑧 𝑑𝑡𝑑𝑧 = 1 两个连续变量 t 和 z 的冲激定义为 §4.5 两个变量的离散傅里叶变换

§4.5两个变量的离散傅里叶变换 。二维冲激及其取样特性一离散变量 二维离散冲激定义 6(x-xo,y -yo) 6(x,y)= x=y=0 other 二维离散冲激也有一维情况下的取样特性 00 ∑∑f8=fo0) X=-00y=-00 00 00 更一般地,位于坐标(xo,y0)处的冲激 ∑fw8-oy-w)=foo X=-00y=-0∞
二维离散冲激也有一维情况下的取样特性 𝑥=−∞ ∞ 𝑦=−∞ ∞ 𝑓 𝑥, 𝑦 𝛿 𝑥, 𝑦 = 𝑓(0,0) 更一般地,位于坐标 𝑥0, 𝑦0 处的冲激 𝑥=−∞ ∞ 𝑦=−∞ ∞ 𝑓 𝑥, 𝑦 𝛿 𝑥 − 𝑥0, 𝑦 − 𝑦0 = 𝑓(𝑥0, 𝑦0) §4.5 两个变量的离散傅里叶变换 𝛿 𝑥, 𝑦 = ቊ 1 , 𝑥 = 𝑦 = 0 0, 𝑜𝑡ℎ𝑒𝑟 二维离散冲激定义 二维冲激及其取样特性—离散变量
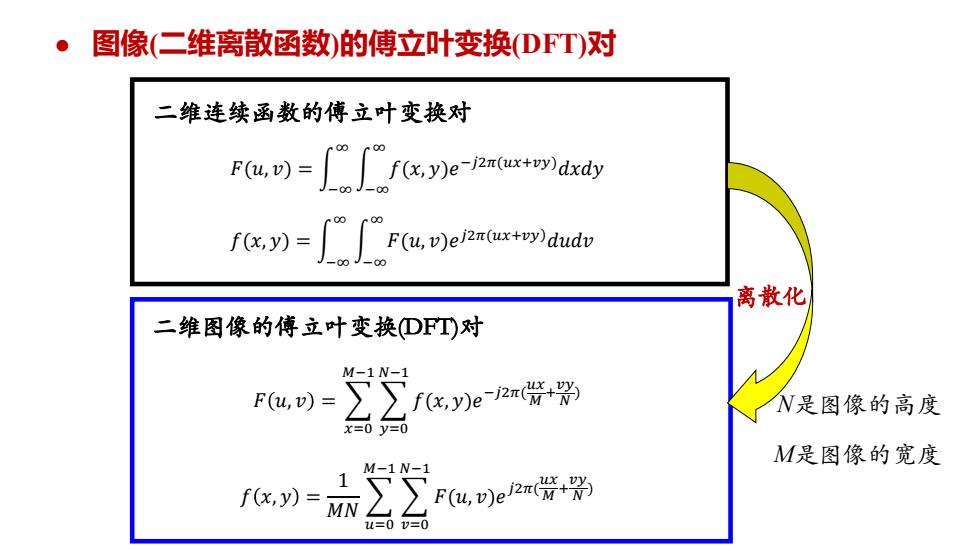
图像(二维离散函数)的傅立叶变换(DFT)对 二维连续函数的傅立叶变换对 Pu=Cf化eauw f,=∫ F(u,v)ejz(uxvy)dudv 离散化 二维图像的傅立叶变换DFT对 M-1N-1 F(u,v)= fx,y)e2π货+为 N是图像的高度 M是图像的宽度 M-1N-1 1 f(x,y)= MN F(u,p)e2r货+ u=00=0
二维连续函数的傅立叶变换对 二维图像的傅立叶变换(DFT)对 离散化 N是图像的高度 M是图像的宽度 𝐹 𝑢, 𝑣 = 𝑥=0 𝑀−1 𝑦=0 𝑁−1 𝑓(𝑥, 𝑦)𝑒 −𝑗2𝜋( 𝑢𝑥 𝑀 + 𝑣𝑦 𝑁 ) 𝑓 𝑥, 𝑦 = 1 𝑀𝑁 𝑢=0 𝑀−1 𝑣=0 𝑁−1 𝐹(𝑢, 𝑣)𝑒 𝑗2𝜋( 𝑢𝑥 𝑀 + 𝑣𝑦 𝑁 ) 图像(二维离散函数)的傅立叶变换(DFT)对 𝑓(𝑥, 𝑦) = න −∞ ∞ න −∞ ∞ 𝐹(𝑢, 𝑣)𝑒 𝑗2𝜋(𝑢𝑥+𝑣𝑦)𝑑𝑢𝑑𝑣 𝐹(𝑢, 𝑣) = න −∞ ∞ න −∞ ∞ 𝑓(𝑥, 𝑦)𝑒 −𝑗2𝜋(𝑢𝑥+𝑣𝑦)𝑑𝑥𝑑𝑦
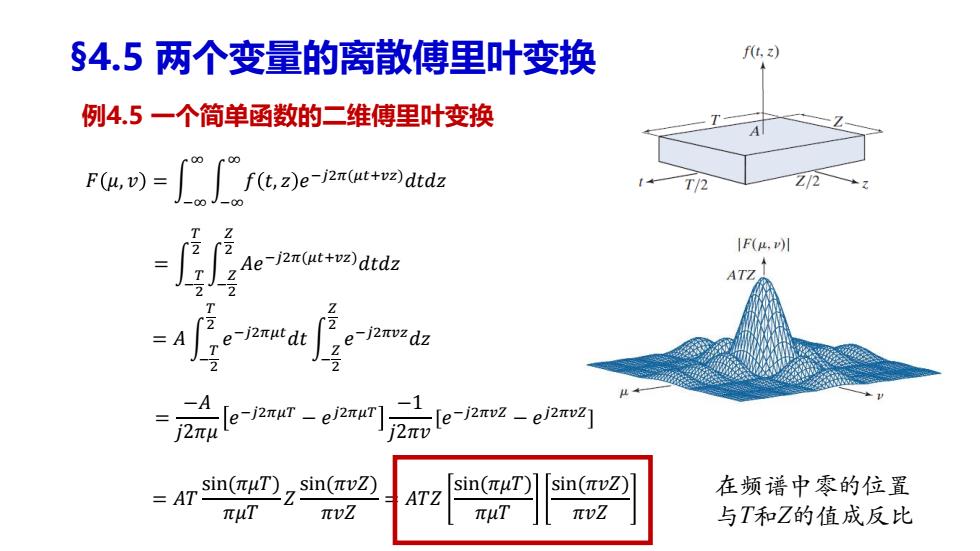
§4.5两个变量的离散傅里叶变换 f(t.z) 例4.5一个简单函数的二维傅里叶变换 P)e-odsds T/2 Z12 -00 |F(μ.川 Ae-j2n(ut+vz)dtdz ATZ =Ae-mtdt 「2 e-j2nvzdz =72er-er品e2-ea叫 -A in(πuT)sin(rv☑ sin(πvZ)l AT ATZ sin(πuT) 在频谱中零的位置 πuT πZ πuT πvZ 与T和Z的值成反比
𝐹 𝜇, 𝑣 = න −∞ ∞ න −∞ ∞ 𝑓 𝑡, 𝑧 𝑒 −𝑗2𝜋(𝜇𝑡+𝑣𝑧)𝑑𝑡𝑑𝑧 = න − 𝑇 2 𝑇 2 න − 𝑍 2 𝑍 2 𝐴𝑒 −𝑗2𝜋(𝜇𝑡+𝑣𝑧)𝑑𝑡𝑑𝑧 = 𝐴 න − 𝑇 2 𝑇 2 𝑒 −𝑗2𝜋𝜇𝑡𝑑𝑡 න − 𝑍 2 𝑍 2 𝑒 −𝑗2𝜋𝑣𝑧𝑑𝑧 = 𝐴𝑇 sin(𝜋𝜇𝑇) 𝜋𝜇𝑇 𝑍 sin(𝜋𝑣𝑍) 𝜋𝑣𝑍 = 𝐴𝑇𝑍 sin(𝜋𝜇𝑇) 𝜋𝜇𝑇 sin(𝜋𝑣𝑍) 𝜋𝑣𝑍 在频谱中零的位置 与T和Z的值成反比 §4.5 两个变量的离散傅里叶变换 例4.5 一个简单函数的二维傅里叶变换 = −𝐴 𝑗2𝜋𝜇 𝑒 −𝑗2𝜋𝜇𝑇 − 𝑒 𝑗2𝜋𝜇𝑇 −1 𝑗2𝜋𝑣 [𝑒 −𝑗2𝜋𝑣𝑍 − 𝑒 𝑗2𝜋𝑣𝑍]