
频率域滤波 ·4.1背景 ·4.2基本概念 ·4.3取样和取样函数的傅立叶变换 ·4.4单变量的离散傅立叶变换 ·4.5两个变量的扩展 ·4.6二维离散傅立叶变换的一些性质 ·4.7频率域滤波基础 ·4.8频率域滤波器平滑图像 ·4.9频率域滤波器锐化图像 ·4.10选择性滤波
• 4.1 背景 • 4.2 基本概念 • 4.3 取样和取样函数的傅立叶变换 • 4.4 单变量的离散傅立叶变换 • 4.5 两个变量的扩展 • 4.6 二维离散傅立叶变换的一些性质 • 4.7 频率域滤波基础 • 4.8 频率域滤波器平滑图像 • 4.9 频率域滤波器锐化图像 • 4.10 选择性滤波 频率域滤波

§4.8频域平滑滤波器 基本思想 图像的边缘和其它灰度变化剧烈的部分对应着频域的高频成分,所以 可以通过减弱高频成分就可以实现图像的平滑(模糊) 基本手段 频域中低通滤波(频域相乘) G(u,v)=H(u,v)F(u,v) 傅里叶变 滤波函数 逆傅里叶 换 H(u,) 变换 F(,) G(u,v)=F(u,v)H(u,v) 平滑的图像 预处理 后处理 f1(x,y)=f(x,y)*(-1)*y =g-1[H(u,v)F(,v)] 关键是H(u,v)设计 f(x,y) 增强后的图像 g(x,y)
频域中低通滤波 (频域相乘) 平滑的图像 §4.8 频域平滑滤波器 基本思想 图像的边缘和其它灰度变化剧烈的部分对应着频域的高频成分,所以 可以通过减弱高频成分就可以实现图像的平滑(模糊) 基本手段 𝑮(𝒖, 𝒗ሻ = 𝑯(𝒖, 𝒗ሻ𝑭(𝒖, 𝒗ሻ = 𝕴 −𝟏 𝑯(𝒖, 𝒗ሻ𝑭(𝒖, 𝒗ሻ 关键是𝑯(𝒖, 𝒗ሻ设计
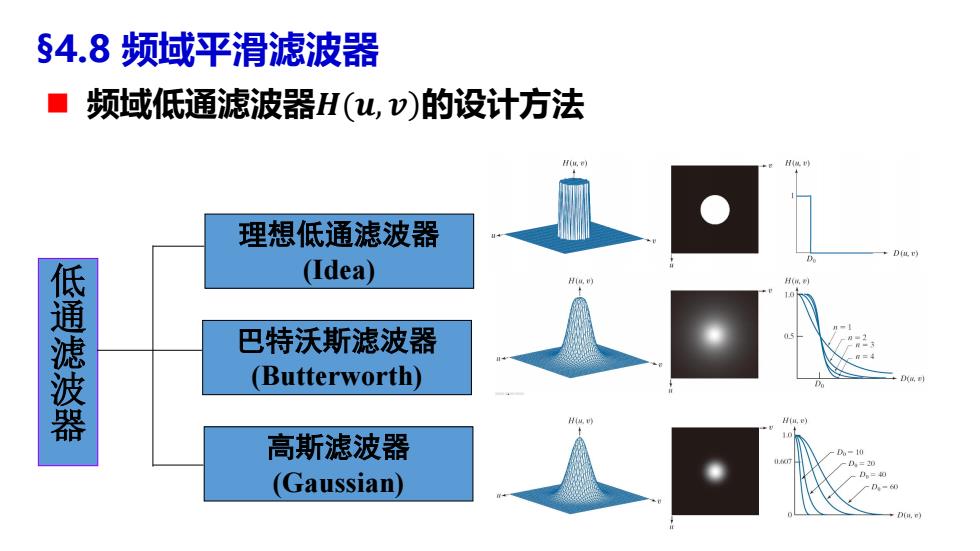
§4.8频域平滑滤波器 ■ 频域低通滤波器H(u,v)的设计方法 H(v) 理想低通滤波器 (Idea) 低通滤波器 巴特沃斯滤波器 (Butterworth) 高斯滤波器 =10 (Gaussian)
频域低通滤波器𝑯(𝒖, 𝒗ሻ的设计方法 理想低通滤波器 (Idea) 巴特沃斯滤波器 (Butterworth) 高斯滤波器 (Gaussian) 低 通 滤 波 器 §4.8 频域平滑滤波器

§4.8.1理想低通滤波器 (Ideal Lowpass Filters) 理想低通滤波器传递函数 方法:从高频处截断,只保留低频部分 H(u,) ifD(u,)≤Do if D(u,v)>Do D(u,) -+6- H(,v) H(u v) 截断频率 (cut-off frequency) Do →D(uv) H(,v)的三维显示 H(4,)的幅频谱图 D(,)是(4,)到原点(0,0)的距离
方法:从高频处截断,只保留低频部分 理想低通滤波器传递函数 截断频率 (cut-off frequency) H(u,v)的三维显示 H(u,v)的幅频谱图 D(u,v)是(u,v)到原点(0,0)的距离 𝐻(𝑢, 𝑣ሻ = ቊ 1 𝑖𝑓𝐷(𝑢, 𝑣ሻ ≤ 𝐷0 0 𝑖𝑓𝐷(𝑢, 𝑣ሻ > 𝐷0 𝐷(𝑢, 𝑣ሻ = 𝑢 − 𝑀 2 2 + 𝑣 − 𝑁 2 2 1Τ2 §4.8.1理想低通滤波器 (Ideal Lowpass Filters)
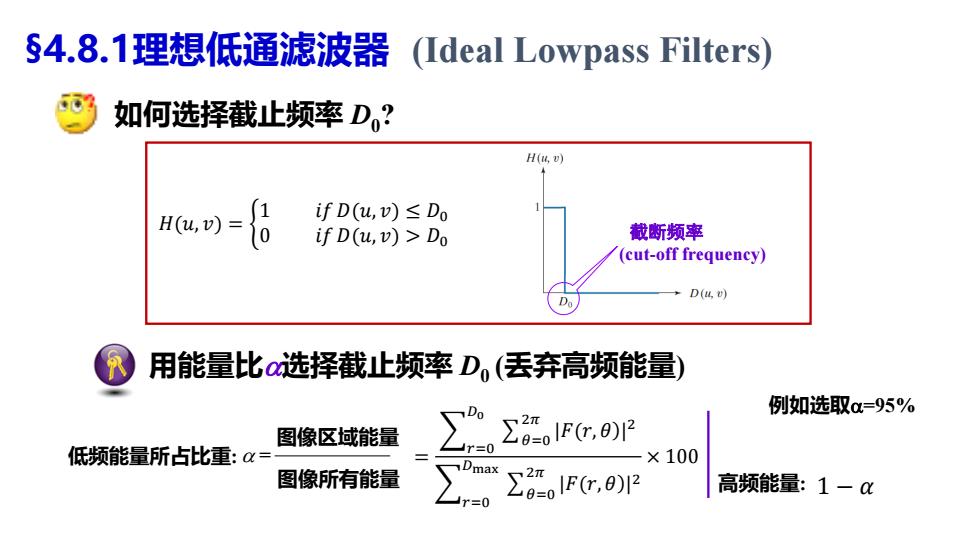
§4.8.1理想低通滤波器 (Ideal Lowpass Filters) 如何选择截止频率D? H(4,D) H(u,)= 1 ifD(u,v)≤Do if D(u,v)>Do 截断频率 (cut-off frequency) →D(4) Da 用能量比a选择截止频率D,(丢弃高频能量) 例如选取α=95% 图像区域能量 低频能量所占比重:α= ×100 图像所有能量 Dmax r=0 ∑ao1Pc,0P 高频能量:1一C
用能量比选择截止频率 D0 (丢弃高频能量) = 图像区域能量 图像所有能量 例如选取=95% 低频能量所占比重: 高频能量: §4.8.1理想低通滤波器 (Ideal Lowpass Filters) 如何选择截止频率 D0? 𝐻(𝑢, 𝑣ሻ = ቊ 1 𝑖𝑓𝐷(𝑢, 𝑣ሻ ≤ 𝐷0 0 𝑖𝑓𝐷(𝑢, 𝑣ሻ > 𝐷0 截断频率 (cut-off frequency) = 𝑟=0 𝐷0 𝜃=0 2𝜋 |𝐹(𝑟, 𝜃ሻ| 2 𝑟=0 𝐷max 𝜃=0 2𝜋 |𝐹(𝑟, 𝜃ሻ| 2 × 100 1 − 𝛼
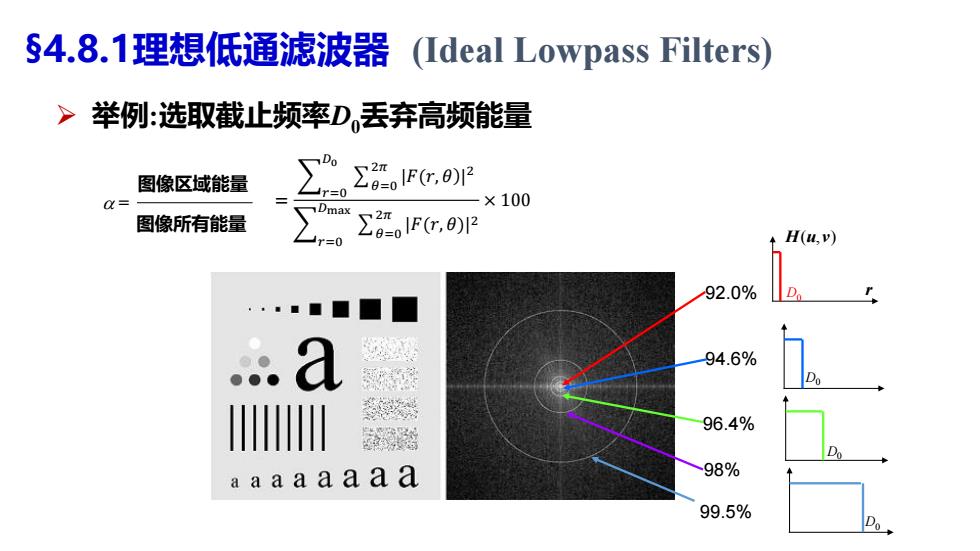
§4.8.1理想低通滤波器 (Ideal Lowpass Filters) >举例:选取截止频率D,丢弃高频能量 图像区域能量 ∑8oIFG,0 X= ×100 Dmax 图像所有能量 》,nΣ6o1F6.8IP H(u,) 92.0% ■ a 94.6% 96.4% aaaaaaaa 98% 99.5%
98% 92.0% r H u v ( , ) D0 94.6% D0 96.4% D0 99.5% D0 §4.8.1理想低通滤波器 (Ideal Lowpass Filters) 举例:选取截止频率D0丢弃高频能量 = 图像区域能量 图像所有能量 = 𝑟=0 𝐷0 𝜃=0 2𝜋 |𝐹(𝑟, 𝜃ሻ| 2 𝑟=0 𝐷max 𝜃=0 2𝜋 |𝐹(𝑟, 𝜃ሻ| 2 × 100
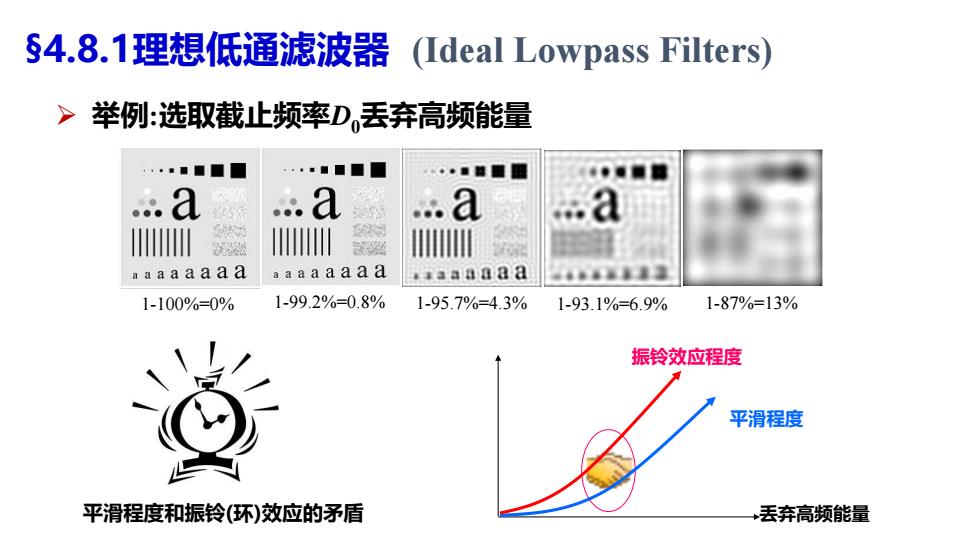
§4.8.1理想低通滤波器(Ideal Lowpass Filters) >举例:选取截止频率D丢弃高频能量 ■■■ ...a ..d aa aaaaaa aa aaaaaa aaaaa 1-100%=0% 1-99.2%=0.8% 1-95.7%=4.3%1-93.1%=6.9% 1-87%=13% 振铃效应程度 平滑程度 平滑程度和振铃(环)效应的矛盾 丢弃高频能量
1-100%=0% 1-93.1%=6.9% 丢弃高频能量 平滑程度 振铃效应程度 1-99.2%=0.8% 1-95.7%=4.3% 1-87%=13% 平滑程度和振铃(环)效应的矛盾 §4.8.1理想低通滤波器 (Ideal Lowpass Filters) 举例:选取截止频率D0丢弃高频能量

§4.8.1理想低通滤波器 (Ideal Lowpass Filters) 理想低通滤波器特点 ·Do半径内的频率分量无损通过 圆外的频率分量被滤除 ·若滤除的高频分量有大量的边缘信息,会导致图像边缘模糊 ·在D,半径包含的范围内包含大部分能量,大部分尖锐细节信 息存在于被去除的能量中 ·被平滑的图像导致一种非常严重的振铃效果
§4.8.1理想低通滤波器 (Ideal Lowpass Filters) • 𝐷0 半径内的频率分量无损通过 • 圆外的频率分量被滤除 • 若滤除的高频分量有大量的边缘信息,会导致图像边缘模糊 • 在𝐷0 半径包含的范围内包含大部分能量,大部分尖锐细节信 息存在于被去除的能量中 • 被平滑的图像导致一种非常严重的振铃效果 理想低通滤波器特点

§4.8.1理想低通滤波器 (Ideal Lowpass Filters) 为什么有振铃效应? a 4#444414a0超0 观察H(4,)的空域形式PSF)可找到直观解释 H( H(u, H(u,v) Frequency Domain +D(4,) h(x) 平滑作用 Spatial Domain h(x.y) Ringing 振铃
H(u,v) Frequency Domain Spatial Domain 平滑作用 Ringing 振铃 h(x) h(x,y) x y x §4.8.1理想低通滤波器 (Ideal Lowpass Filters) 为什么有振铃效应? 观察H(u,v)的空域形式(PSF)可找到直观解释

§4.8.1理想低通滤波器 (Ideal Lowpass Filters) 为什么有振铃效应? .a 44444a0a社 观察H(u,)的空域形式PSF)可找到直观解释 卷积滤波 原始图像(黑色背景上有5个脉冲) 滤波图像
原始图像(黑色背景上有5个脉冲) 滤波图像 卷积滤波 §4.8.1理想低通滤波器 (Ideal Lowpass Filters) 为什么有振铃效应? 观察H(u,v)的空域形式(PSF)可找到直观解释