
第3章灰度变换与空间滤波 它的与众不同之处在于,是透过光线看阴影还是透过阴影看亮度」 一大卫·林赛 引言 术语空间域指图像平面本身,这类图像处理方法直接以图像中的像素操作为基础。这是相对于 变换域中的图像处理而言的,正如2.6.7节所介绍的和第4章将要详细讨论的那样,变换域的图像处 理首先把一幅图像变换到变换域,在变换域中进行处理,然后通过反变换把处理结果返回到空间域。 空间域处理主要分为灰度变换和空间滤波两类。正像本章您将了解到的那样,灰度变换在图像的单个 像素上操作,主要以对比度和阂值处理为目的。空间滤波涉及改善性能的操作,如通过图像中每一个 像素的邻域处理来锐化图像。接下来几节我们将讨论一些经典的灰度变换和空间滤波技术。我们还将 讨论模糊技术的某些细节,以便允许我们在灰度变换和空间滤波算法的公式化表示中并人不太精确的 以知识为基础的信息。 3.1背景知识 3.1.1灰度变换和空间滤波基础 本节讨论的所有图像处理技术都是在空间域进行的。由2.4.2节的讨论,我们知道空间域就是简 单的包含图像像素的平面。如2.6.7节定义的那样,与(第4章的主题)频率域相反,空间域技术直 接在图像像素上操作,例如,对于频率域来说,其操作在图像的傅里叶变换上执行,而不针对图像本 身。正如您将在阅读全书的过程中了解到的那样,某些图像处理任务在空间域中执行更容易或更有意 义,而另一些任务则更适合使用其他方法。通常,空间域技术在计算上更有效,且在执行上需要较少 的处理资源。 本章讨论的空间域处理可由下式表示: g(x,y=TLf(x,y川 (3.1-1) 其中f(x,y)是输入图像,g(x,y)是处理后的图像,T是在点(x,y)的 有时也使用其他形状的邻碱。如 邻域上定义的关于∫的一种算子。算子可应用于单幅图像(本章中我 圆的数 近似。 矩形邻域是到 们的主要关注点)或图像集合,例如,如2.6.3节中讨论的那样,为降 前为止最好的邻域,因为它们在 算机上实现起来更为容易

第3章灰度变换与空间滤波 63 低噪声而对图像序列执行逐像素的求和操作。图3.1显示了式(3.1)在单幅图像上的基本实现。所示 的点(化,)是图像中的一个任意位置,包含该点的小区域是点(xy)的邻,如2.65节解释的那样。 典型地,邻城是中心在(x,y)的矩形.其尺寸比图像小得多 图3.1中给出的处理由以下几北组成:邻域原点从一 原点 个像素向另一个像素移动。对邻域中的像素应用算子T】 并在该位置产生恰出。这样,对于任意指定的位置(x,v) c.y 输出图像g在这些坐标处的值就等于对∫中以(x,)为原 (化)的3×3邻城 点的邻域应用算子T的结果。例如,假设该邻城是大小为 3×3的正方形.算子T定义为“十算该邻域的平均灰度” 图像 考虑图像中的任意位置,譬如000,150)。假设该邻域的 空间域 原点位于其中心处,则在该位置的结果g100,150)是计算 100,150)和它的8个邻点的和,再除以9(即由邻域包 图3】空间域图像中关于点(化,y)的一个 围的像素灰度的平均值)。然后,邻域的原点移动到下 3×3邻域邻域在车图像中从个像个素 个位置,并重复前面的过程,产生下一个输出图像g的值 到另一个像素移动来生成一幅输出图像 典型地,该处理从输入图像的左上角开始以水平扫描的方式逐像素地处理,每次一行。当该邻域的 原点位于图像的边界上时,部分邻域将位于图像的外部。此时,不是在用T做指定的计算时忽略外侧 邻点,就是用0或其他指定的灰度值填充图像的边缘。被填充边界的厚度取决于邻域的大小。在3.4, 节中,我们将再回到这一问题 就像我们在3.4节中羊细计论的那样。则网则描术的时程称为空间滤波,其中,邻域与陌定义的操 作一起称为空间滤波器(也称为空间模核模板或窗口)。在邻域中执行的操作类型决定了滤波处 理的特性。 最小邻域的大小为1×1。在这种情祝下,8仅取决于点(x)处的∫值,而式(3.1)中的T则成 为一个形如下式的灰度(也称为灰度级或映射)变换函数: s=T(r) (3.1-2 其中,为表达方便,令r和s分别表示变量,即g和f在任意点(x,y)处的灰度。例如,如果T)有 如图3.2()所示的形式,对∫中每一个像素施以变换产生相应的8的像素的效果将比原始图像有更高 的对比度,即低于k的灰度级更暗,而高于k的灰度级更亮。这种技术有时称为对比度拉伸(见3.2.4 节),在该技术中,低于k的r值被变换函数压缩在一个较窄的范围s内。接近黑色:而高于k的,值 则与此相反。很明显,灰度值经映射得到了相应的值。。在如图3.26)所示的极限情况下,T) 产生了一幅两级(二饱图像。这种形式的映射称为闲值处理函数。有些相当简单但功能强大的处理方 法,可以使用灰度变换函数用公式加以表达。在这一章中,我们主要使用灰度变换函数来进行图像增 强。在第0章中,我们将使用灰度变换函数来进行图像分割。其结果仅取决于一个点处的灰度的方 法有时称为,点处理技术,与此相反,本节早些时候讨论的方法则称为邻域处理技术。 3.1.2关于本章中的例子 虽然灰度变换和空间滤波覆盖了相当宽的应用范围,但本章中的多数例子是图像增强应用。增 强处理是对图像进行加工,使其结果对于特定的应用比原始图像更合适的一种处理。“特定” 一词在 这里很重要,它一开始就确定增强技术是面向问题的。例如,对于增强X射线图像非常有用的方法, 可能并不是增强由电磁波谱中远红外波段拍摄的图像的最好方法。图像增强没有通用的“理论”。当2可 为视觉解释而处理幅图像时。观察者将是判定一种特定方法好与坏的最终栽判员。在处理机器感知园

64 数字图像处理(第三版) 时,一种给定的技术很易于量化。例如,在自动字符识别系统中,最合适的增强方法就是可得到最好 识别名的方法,这里不考虑一种方法较另一种方法的计算量的要求。 ab s=T() s■7() T()- T(n) 暗人亮 图32灰度变换函数:(对比度拉伸函数:6)闲值处理函数 然而,不管应用或使用过的方法,图像增强是视觉上最具吸引力的图像处理领域之一。理所当 然地,图像处理的初学者通常会寻找重要的且理解起来相对简单的增强应用。因此,使用图像增强的 例子来说明本章中论述的空间处理方法,不仅可以节省本书中处理图像增强的额外的章节,而且更重 要的是对初学者介绍空间域处理技术的细节的更有效方法。正如您将要看到的那样,随着本书的进程 本章叙述的基本内容可用于比图像增强宽得多的范围。 3.2 一些基本的灰度变换函数 灰度变换是所有图像处理技术中最简单的技术。?和5分别代表处理前后的像素值。如前一节指 出的那样,这些值与s=)表达式的形式有关,其中T是把像素值r映射到像素值s的一种变换。由 于我们处理的是数字量,所以变换函数的值通常存储在一个一维阵列中,且从到s的映射是通过查 找表实现的。对于8比特环境,包含T的值的一个查找表将有256条记录。 作为关于灰度变换的介绍,考虑图33,该图显示了图像增强常用的三类基本函数:线性函数(反 转和恒等变换)、对数函数(对数和反对数变换)和幂律函数(n次幂和n次根变换)。恒等函数是最一 般的情况,其输出灰度等于输人灰度的变换,在图3.3中包括它仅仅为了完整性考虑。 3.2.1图像反转 使用图3.3中所示的反转变换,可得到灰度级范围为0,L-的一幅图像的反转图像,该反转图 像由下式给出: s=L-1-r (3.2.1 使用这种方式反转一辐图像的灰度级,可得到等效的照片底片。这种类型的处理特别适用于增强嵌入 在一幅图像的暗区域中的白色或灰色细节,特别是当黑色面积在尺寸上占主导地位时。图3.4显示了 一个例子。原图像是一幅数字乳房X射线照片,其中显示有一小块病变。尽管事实上两幅图在视觉 内容上都一样,但应注意,在这种特殊情况下,分析乳房组织时使用反转图像会容易得多 3.2.2对数变换 图 图3.3中的对数变换的通用形式为 s=clog(+r) (3.2-2)
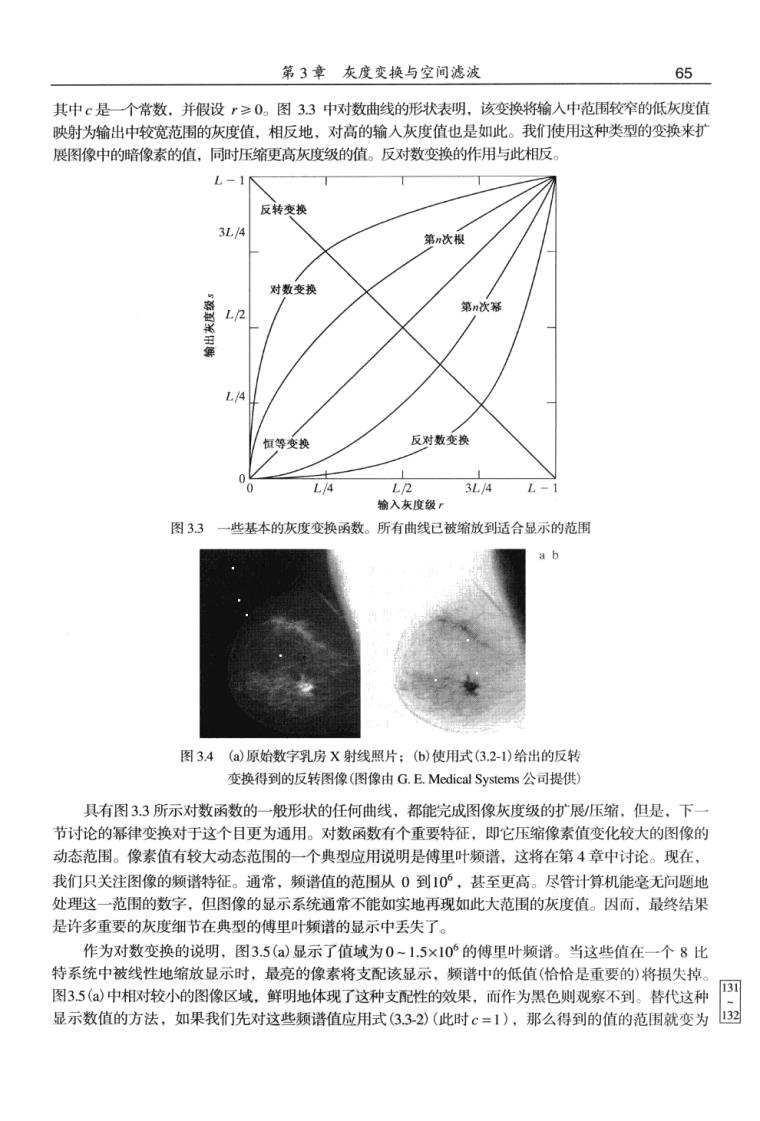
第3章灰度变换与空问滤波 65 其中是一个常数.并假设r≥0。图33中对数曲线的形状表明.该变换将输入中范围较窄的低灰度值 映射为输出中较宽范围的灰度值,相反地,对高的输入灰度值也是如此。我们使用这种类型的变换来剁 展图像中的暗像素的值,同时压缩更高灰度级的值。反对数变换的作用与此相版。 L-10 反转变换 3L/4 第n次根 对数变换 第次 反对数变换 3L4 L- 输入灰度级r 图33一些基本的灰度变换函数。所有曲线已被缩放到适合品示的范围 a b 图34(a原始数字乳房X射线照片:(6)使用式(3.2-1)给出的反转 变换得到的反转图像(图像由G.E.Medical Systems公司提供) 具有图3.3所示对数函数的一般形状的任何曲线,都能完成图像灰度级的扩展压缩,但是,下一 节讨论的幂律变换对于这个目更为通用。对数函数有个承要特征,即它压缩像素值变化较大的图像的 动态范围。像素值有较大动态范围的一个典型应用说明是傅里叶频谱,这将在第4章中讨论。现在。 我们只关注图像的矩礼特征。通常.额滤情的节围从0到10其至申高。尽管十值机能宴无问颗地 处理这一范围的数字,但图像的显示系统通常不能如实地再现如此大范围的灰度值。因而,最终结 是许多重要的灰度细节在典型的傅里叶频谱的显示中丢失了。 作为对数变换的说明,图3.5(a)显示了值域为0-1.5×10°的傅里叶频谱。当这些值在一个8比 特系统中被线性地缩放显示时,最亮的像素将支配该显示,频谱中的低值(恰恰是重要的)将损失掉。 图35(a)中相对较小的图像区域,鲜明地体现了这种支配性的效果,而作为黑色则观察不到。替代这种 显示数值的方法,如果我们先对这些频谱值应用式(3.32》(此时=1),那么得到的值的范围就变为 图
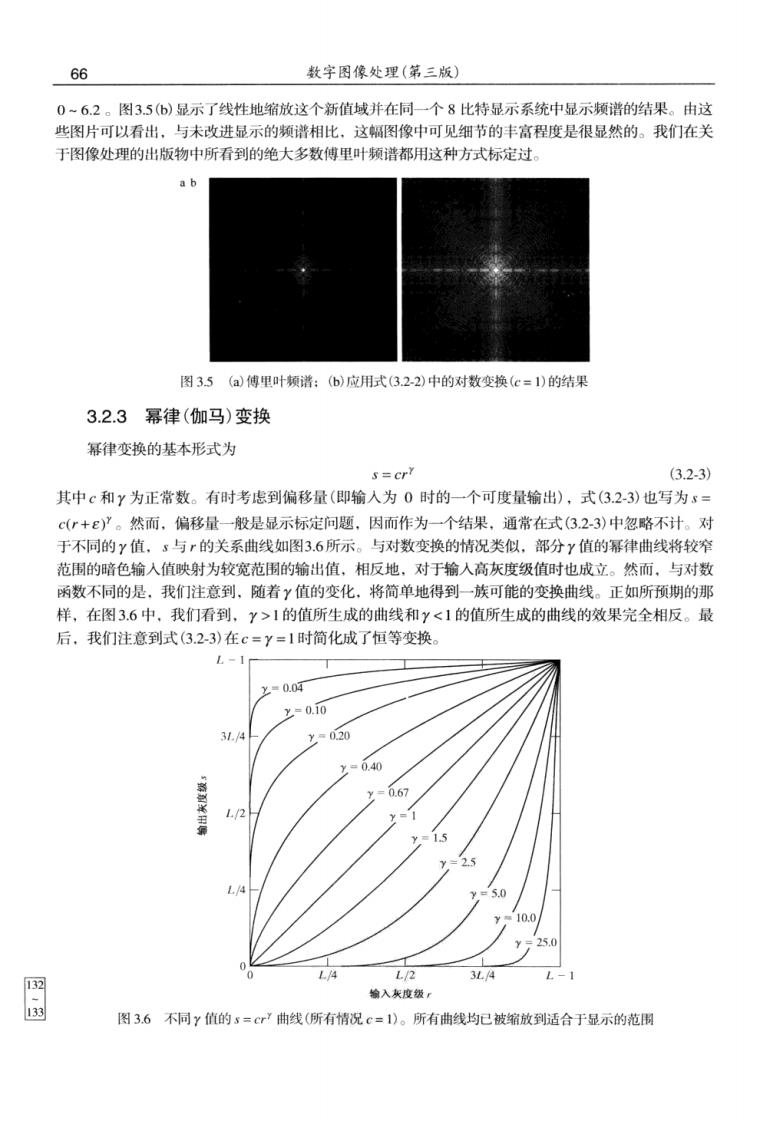
66 数字图像处理(第三版) 0一6.2。图35(6)显示了线性地缩放这个新值域并在同一个8比特显示系统中显示频谱的结果。由这 些图片可以看出,与未改进显示的频谱相比.这幅图像中可见细节的丰富程度是很显然的。我们在关 于图像处理的出版物中所看到的绝大多数傅里叶颜谱都用这种方式标定过。 ab 图35(a)傅里叶频谱:(b)应用式(3.2-2)中的对数变换(c=1)的结果 3.2.3幂律(加马)变换 幂律变换的基本形式为 s=cr (323) 其中c和y为正常数。有时考虑到偏移量(即输入为0时的一个可度量输出),式(3.23)也写为s c(r+ε了。然而,偏移量一般是显示标定问题,因而作为一个结果.通常在式3.2-3)中忽略不计。对 于不同的y值,s与r的关系曲线如图3.6所示 与对数变换的情祝类似,部分Y值的幂律曲线将较 范围的暗色输入值映射为较宽范围的输出值,相反地,对于输人高灰度级值时也成立。然而,与对数 函数不同的是,我们注意到.随着Y值的变化,将简单地得到一族可能的变换曲线。正如所预期的那 样,在图3.6中,我们看到,Y>1的值所生成的曲线和y<1的值所生成的曲线的效果完全相反。最 后,我们注意到式(3.23)在c=Y=1时简化成了恒等变换。 L-1 y=0.10 31. 040 667 15 2 入灰度级 图36不同y值的s='曲线(所有情况c=)。所有曲线均已被缩放到适合于显示的范围

第3章灰度变换与空间滤波 67 用于图像获取、打印和显示的各种设备根据幂律来产生响应。习惯上,幂律方程中的指数称为 伽马[故在式(3,2-3)中使用这一符号。用于校正这些幂律响应现象的处理称为伽马校正。例如,阴 极射线管(CRT)设备有一个灰度-电压响应,该响应是一一个指数变化范围约为1.8~2.5的幂函数。在 图3.6中,用y=25时的参考曲线,我们看到,这种显示系统产生的图像往往要比期望的图像暗。这 个结果在图3.7加以说明。图3.7()显示了喻人到监视器的简单灰度斜坡(渐变)图像。如期塑的那 样,监视器表现了输出比输入暗,如图3.76)所示。在这种情况下,伽马校正很简单。我们需要做的只 是将图像输人到监视器前进行预处理,即进行s=2=+变换。结果如图3.7(©)所示。当输入到相同 的监视器时,这一伽马校正过的输入产生外观上接近于原图像的输出.如图3.7(@)所示。类似的分析也 适用于其他图像设备,如扫描仪和打印机。唯一的不同是随设备而定的伽马值(Poyntonl1996。 8 原像 在监视器上观黎到的原图像 经马校正后的图像 药供号批是士型 图3.7(a亮度斜坡图像:(b)具有伽马值为25的模拟监视器上观察到的图像:()经伽马校 正后的图像:(d在同一监挽器上观察到的经伽马校正后的图像。比较图(和图(a 如果所关注的是在计算机屏幕上精确显示图像,则伽马校正是很重要的。不恰当校正的图像看 起不是太亮,就是太暗。试图精确再现彩色也需要伽马校正的一些知识,因为改变伽马值不仅会改变 亮度,而且会改变彩色图像中红、绿、蓝的比率。随着数字图像在互联网上商业应用的增多,在过去几 年里,伽马校正逐渐变得越来越重要。为流行网站创建被几百万人浏览的图像是很平常的事。因为大多 数浏览者会有不同的监视器和/或监视器设置。有些计算机系统甚至会内置部分伽马校正。此外.目前 的图像标准并不包含创建图像的伽马值,因此,问题进一步复杂化了。由于这些限制.当在网站中存 储图像时 种合理的方法是用伽马值对图像进行预处理,此伽马值代表了在开放的市场中,在任意 给定时间点,各种型号的监视器和计算机系统所期望的“平均值” 除伽马校正 和脊髓受到影响的一幅核磁共振MR)图像。在胸椎垂直中心附近,即图中从上往下约14处,骨折显而 易见。由于所给图像整体偏暗,因而需要扩展灰度级。这可以使用指数为分数的幂律变换来完成。使用 式(3,2-3)给出的幂律变换来处理图3.8(a),得到示于图中的其他几幅图像。对应于图b)到图(的伽马值 135
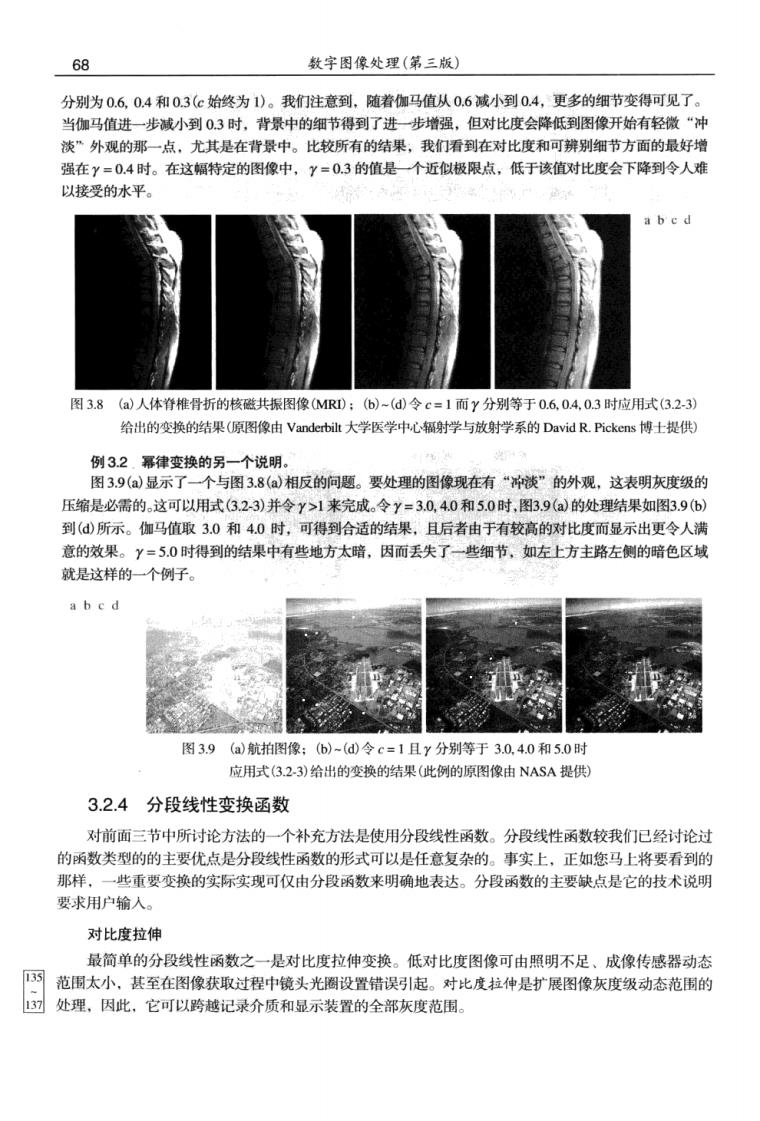
68 数字图像处理(第三版) 分别为0.60,4和0.3(c始终为1)。我们注意到,随着伽马值从0.6减小到0.4,更多的细节变得可见了。 当伽马值进一步诚小到0.3时,背景中的细节得到了进一步增强,但对比度会降低到图像开始有轻微“冲 淡”外观的那一点,尤其是在背景中。比较所有的结果,我们看到在对比度和可辨别细节方面的最好增 强在y=0.4时。在这幅特定的图像中,Y=0.3的值是一个近似极限点,低于该值对比度会下降到令人难 以接受的水平。 a b e d 图3.8(a)人体脊椎骨折的核磁共振图像MRD:(6)-(@令c=1而y分别等于0.60.4,0.3时应用式(3.2-3) 给出的换的结果(原图像由vanderb大学医学中心,辐学与放射学系的David R.Pickens博十提供) 例32.冪律变换的另一个说明。 图3.9()显示了一个与图3.8()相反的向题。要处理的图像现在有“淡”的外观,这表明灰度级的 压缩是必需的。这可以用式3.23)并令y>1来完成。令y=30,40和5.0时,图3,9(a)的处理结果如图3.9(6) 到(所示。伽马值取3.0和4.0时,可得到合适的结果,且后者由于有较高的对比度而显示出更令人满 意的效果。y=5.0时得到的结果中有些地方太暗。.因而丢失了一些细节,如左上方主路左测的暗色区域 就是这样的一个例子 a b e d 图3.9(a)航拍图像:(b)-()令c=1且y分别等于3.0.4.0和5.0时 应用式(3.2.3)给出的变换的结果(此例的原图像由NASA提供 3.2.4分段线性变换函数 对前面三节中所讨论方法的一个补充方法是使用分段线性函数。分段线性函数较我们已经讨论过 的函数类型的的主要优点是分段线性函数的形式可以是任意复杂的。事实上,正如您马上将要看到的 那样。 些重要变换的实际实现可仅由分段函数来明确地表达。分段函数的主要缺点是它的技术说明 要求用户输入。 对比度拉伸 最简单的分段线性函数之一是对比度拉伸变换。低对比度图像可由照明不足、成像传感器动态 网范围太小,甚至在图像获取过程中镜头光圈设置错误马引起。对比度拉仲是扩展图像灰度级动态范围的 园处理,因此。它可以跨越记录介质和显示装置的全部灰度范围
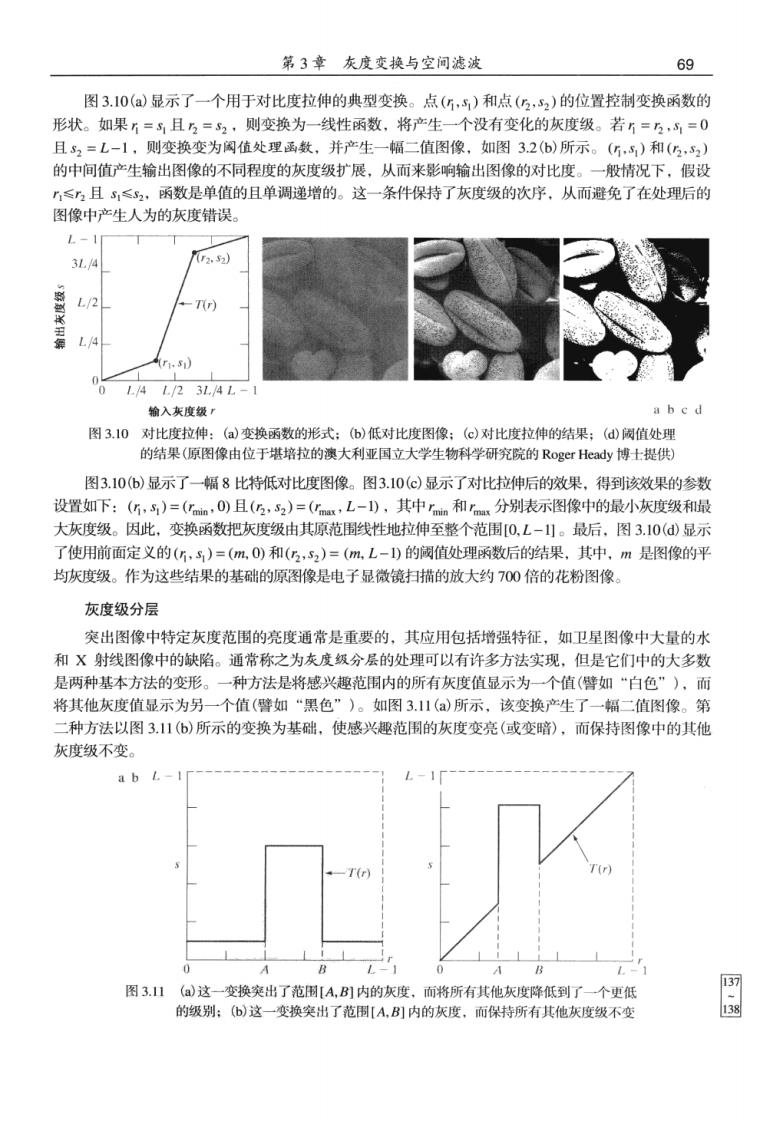
第3章灰度变换与空间滤波 69 图3.10(a)显示了一个用于对比度拉伸的典型变换。点(G,)和点(,52)的位置控制变换函数的 形状。如果万=5且与=52,则变换为一线性函数,将产生一个没有变化的灰度级。若万=2,=0 且马2=L-1,则变换变为阀值处理函数,并产生一幅二值图像,如图326)所示。(G,)和(2,一 的中间值产生输出图像的不同程度的灰度级扩展,从而来影响输出图像的对比度。一般情况下,假设 ”≤且5,≤,函数是单值的且单调递增的。这一条件保持了灰度级的次序,从而避免了在处理后的 图像中产生人为的灰度错误。 L-1 3L4 r.s) L/2 -T) 1/4L./23L./4L. 输入灰度级r a b c d 图3.10对比度拉伸:(a)变换函数的形式;(b)低对比度图像:(C)对比度拉伸的结果;(d阀值处理 的结果(原图像由位于堪培拉的澳大利亚国立大学生物科学研究院的Roger Heady博士提供) 图3.10()显示了一幅8比特低对比度图像。图3.10()显示了对比拉伸后的效果得到该效果的参 设置如下:(G,)=(m,0)且(,2)=(心,L-1),其中r和r分别表示图像中的最小灰度级和最 大灰度级。因此,变换函数把灰度级由其原范围线性地拉伸至整个范围0.L-】。最后,图3.10()显示 了使用前面定义的(,s)=(m0)和(,52)=(m,L-1)的阔值处理函数后的结果,其中,m是图像的平 均灰度级。作为这些结果的基础的原图像是电子显微镜扫描的放大约700倍的花粉图像 灰度级分层 突出图像中特定灰度范围的亮度通常是重要的,其应用包括增强特征,如卫星图像中大量的水 和X射线图像中的缺陷。通常称之为灰度级分层的处理可以有许多方法实现,但是它们中的大多数 是两种基本方法的变形。 一种方法是将感兴趣范围内的所有灰度值显示为一个值(譬如“白色”),而 将其他灰度值显示为另一个值(譬如“黑色”)。如图3.11(a)所示,该变换产生了一幅二值图像。第 二种方法以图3.11(6)所示的变换为基础,使感兴趣范围的灰度变亮(或变暗),而保持图像中的其他 灰度级不变。 a b L-I -1P 图3.山(a这一变换突出了范围[A,B刷内的灰度,而将所有其他灰度降低到了一个更低 的级别:(6)这一变换突出了范周[A,B)内的灰度,而保持所有其他灰度级不变
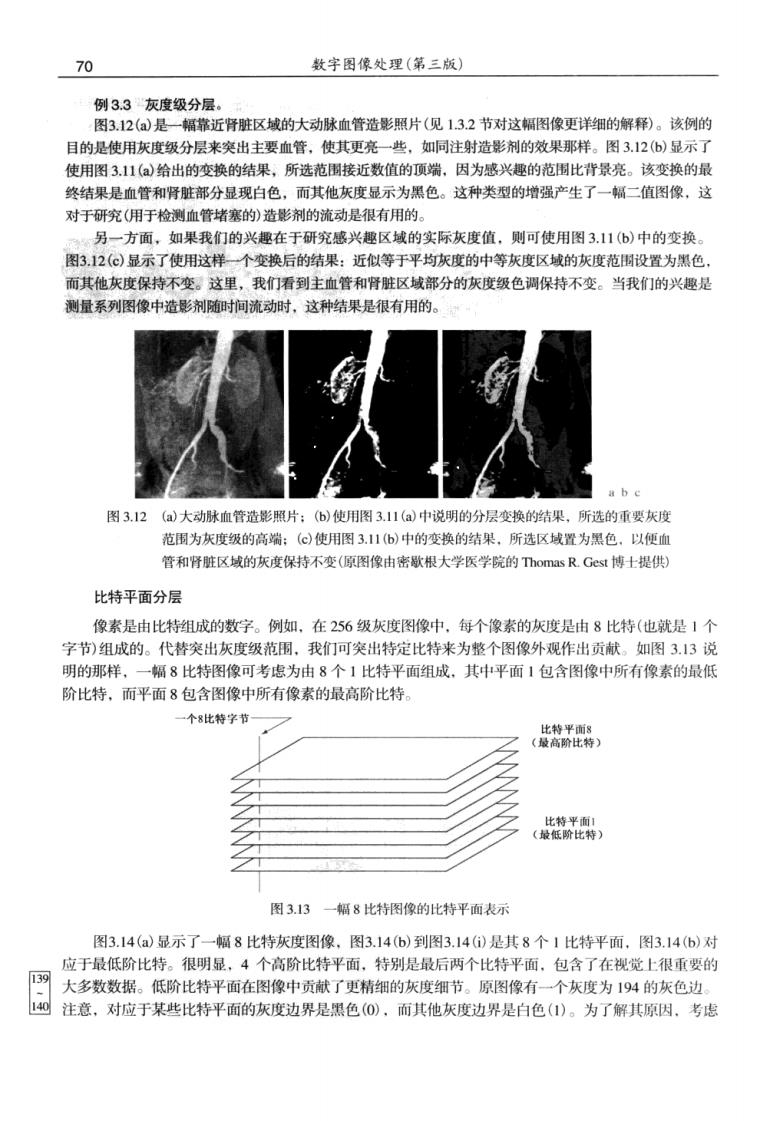
70 数字图像处理(第三版) 制33灰度级分层 图3.12(是一幅靠近肾脏区域的大动脉血管造影照片(见13,2节对这幅图像更详细的解释)。该例的 目的是使用灰度级分层来突出主要血管,使其更亮一些,如同注射造影剂的效果那样。图3.126)显示了 使用图3.11(给出的变换的结果,所选范围接近数值的顶端.因为感兴趣的范围比背最亮。该变换的最 终结果是血管和肾脏部分显现白色,而其他灰度显示为黑色。这种类型的增强产生了一辐二值图像,这 对于研究(用于检测血管堵塞的)造影剂的流动是很有用的。 另一方面,如果我们的兴趣在于研究感兴趣区域的实际灰度值,则可使用图3.11(6)中的变换 图3.12(⊙)显示了使用这样个变换后的结果:近似等于平均灰度的中等灰度区城的灰度范围设置为黑色, 而其他灰度保持不变。这里,我们看到主血管和肾脏区域部分的灰度级色调保持不变。当我们的兴趣是 测量系列图像中造影剂随时间流动时。这种结果是很有用的 b 图3.12()大动脉血管造影照片:(6)使用图3,11(a)中说明的分层变换的结果所选的重要灰度 范围为灰度级的高端:(©)使用图3.11(6)中的变换的结果,所选区城置为黑色.以便血 管和肾脏区城的灰度保持不变(原图像由密数根大学医学院的Thomas R.Gest博十提供) 比特平面分层 像素是由比特组成的数字。例如,在256级灰度图像中,每个像素的灰度是由8比特(也就是1个 字节)组成的。代替突出灰度级范围。我们可突出特定比特来为整个图像外观作出贡献。如图3.13说 明的那样,一幅8比特图像可考虑为由8个1比特平面组成,其中平面1包含图像中所有像素的最低 阶比特,而平面8包含图像中所有像素的最高阶比特。 一个8比特字节 ) 图3.13一幅8比特图像的比特平面表示 图3.14(a)显示了一幅8比特灰度图像,图3.14(6)到图3.14①)是其8个1比特平面,图3.14(b)对 应于最低阶比特。很明显,4个高阶比特平面,特别是最后两个比特平面,包含了在视觉上很重要的 网大多数数据。低阶比特平面在图像中贡献了更精细的灰度细节。原图像有一个灰度为194的灰色边 L40注意。对应于某些比特平面的灰度边界是黑色(O),而其他灰度边界是白色(1)。为了解其原因。考虑

第3章灰度变换与空间滤波 71 一个像素,譬如,图3.14(a)的最低边界的中部。从最高阶平面开始,这些比特平面中的相应像索的 值分别为11000010,它是十进制数194的二进制表示。原图像中任意一个像素的值,可以类似地 由这些比特平面中对应的二进制像素值来重建。 图3.14一幅大小为500×1192像索的8比特灰度图像:)-(比特平面1到8 其中比特平面1对应于最低阶比特。每个比特平面都是一幅二值图像 根据灰度变换函数,显示一幅8比特图像的第8个比特平面并不闲难,它可用阀值灰度变换函 数处理输入图像得到二值图像,该函数将0-127之向的所有灰度映射为0.而将128-255之间的所有 灰度映射为1。图3.14(①)中的二值图像就是使用这种方式得到的。得到生成其他比特平面的灰度变换 数的方法,将作为一个练习留给读者(见习题3.4) 把一幅图像分解为比待平面,对于分析图像中每个比特的相对重要性是很有用的.这一处理可 帮助我们确定用于量化该图像的比特数的充分性。此外,这种类型的分解对图像压缩(第8章的主题) 也很有用,在图像压缩中,重建一幅图像时所用的平面要比全部平面少。例如,图3.15(a)显示了使用 比特平面8和比特平面7重建的一幅图像。重建是使用第n个平面的像素乘以常数2来完成的。与 把第刀个有意义的二进制比特变换成十进制相比,这并没有做更多的事。所用的每个比特平面与一个 相应的常数相乘,然后将所有的比特平面相加得到灰度图像。这样,为得到图3.15(a),我们用128乘 以比特平面8,用64乘以比特平面7,然后把这两个比特平面相加。虽然原图像的主要特征被复原了 但重建后的图像显得有些平淡,特别是在背景区域。这并不奇怪,因为两个平面仅能产生4个不同的 灰度级。把平面6加入到重建中可改善这种情祝.如图3.15(6)所示。注意,该图像的肯景有可感知 的伪轮廓。这一效应可通过在重建中加入第5个平面来显著降低,如图3.15()所示。在重建中使用 更多的平面对图像的外观不会有更大的贡献。因而,我们可以得出这样的结论:存储4个高阶比特平 面将允许我们以可接受的细节来重建原图像。存储这4个平面代替原始图像可减少50%的存储量(不 考虑存储体系结构问题) a b 图315(使用比特平面8和7重建的图像:()使用比特平面87和6重建的图修 ©使用比特平面8,7,6和5重建的图像。将图(@与图3.14(a)进行比较