
第七章 图 本章介绍另一种非线性数据结构一 图 图:是一种多对多的结构关系,每个元素可以有零 个或多个直接前趋;零个或多个直接后继;
本章介绍另一种非线性数据结构 —— 图 图:是一种多对多的结构关系,每个元素可以有零 个或多个直接前趋;零个或多个直接后继;

四 第七章图 7.1图的概念 7.2图的存储结构 7.3图的遍历 7.4生成树 7.5最短路径 7.6拓扑排序
第七章 图 7.1 图的概念 7.2 图的存储结构 7.3 图的遍历 7.4 生成树 7.5 最短路径 7.6 拓扑排序

第七章 图 单 7.1 图的概念 图的概念 二 图的应用 三 图的基本术语
7.1 图的概念 一 图的概念 二 图的应用 三 图的基本术语 第七章 图

图的抽象数据类型定义 ADT Graph{ 数据对象V:V是具有相同特性的数据元 素的集合,称为顶点集。 数据关系R: R=(VR} VR={Kv,w>V,w∈V且表 示从V到w的弧,调词P(V,W)定义了弧 〈V,w)的意义或信息}
图的抽象数据类型定义 ADT Graph{ 数据对象V:V是具有相同特性的数据元 素的集合,称为顶点集。 数据关系R: R={VR} VR={|v,w∈ V且 表 示从v到w的弧,谓词P(v,w)定义了弧 的意义或信息}

基本操作 结构的建立和销毁 对顶点的访问操作 插入或删除顶点 插入和删除弧 对邻接点的操作 遍历1
结构的建立和销毁 插入或删除顶点 对邻接点的操作 对顶点的访问操作 遍历 插入和删除弧 基本操作

图的定义: 图是由一个顶点集V和一个弧集VR构成 的数据结构。 Graph (V,VR) 其中,VR={Kv,w>v,w∈V且P(wW)} 表示从v到w的一条弧,并称v 为弧尾,w为弧头。 谓词P(v,w)定义了弧的意义或信息
图是由一个顶点集 V 和一个弧集 VR 构成 的数据结构。 Graph = (V,VR) 其中,VR={| v,w∈V 且 P(v,w)} 表示从 v 到 w 的一条弧,并称 v 为弧尾,w 为弧头。 谓词 P(v,w) 定义了弧 的意义或信息。 图的定义:
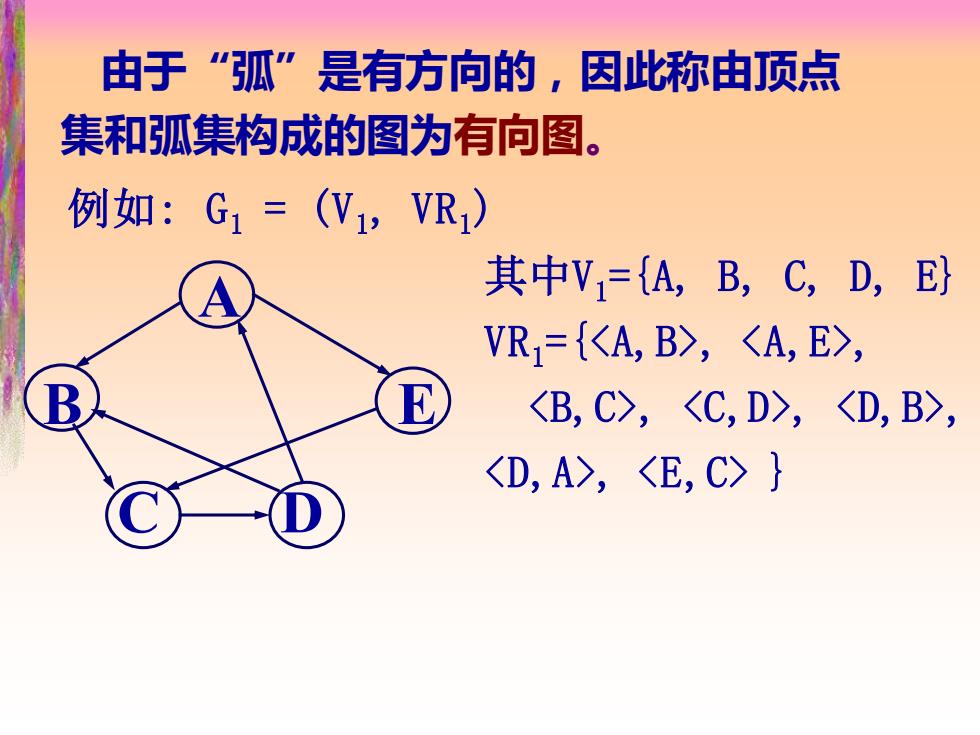
由于“弧”是有方向的,因此称由顶点 集和弧集构成的图为有向图。 例如:G1=(W1,VR) 其中V={A,B,C,D,E卧 VR={KA,B>,〈A,E>, ,C,D>,, ,}
A B E C D 例如: G1 = (V1, VR1) 其中V1={A, B, C, D, E} VR1={, , , , , , } 由于“弧”是有方向的,因此称由顶点 集和弧集构成的图为有向图
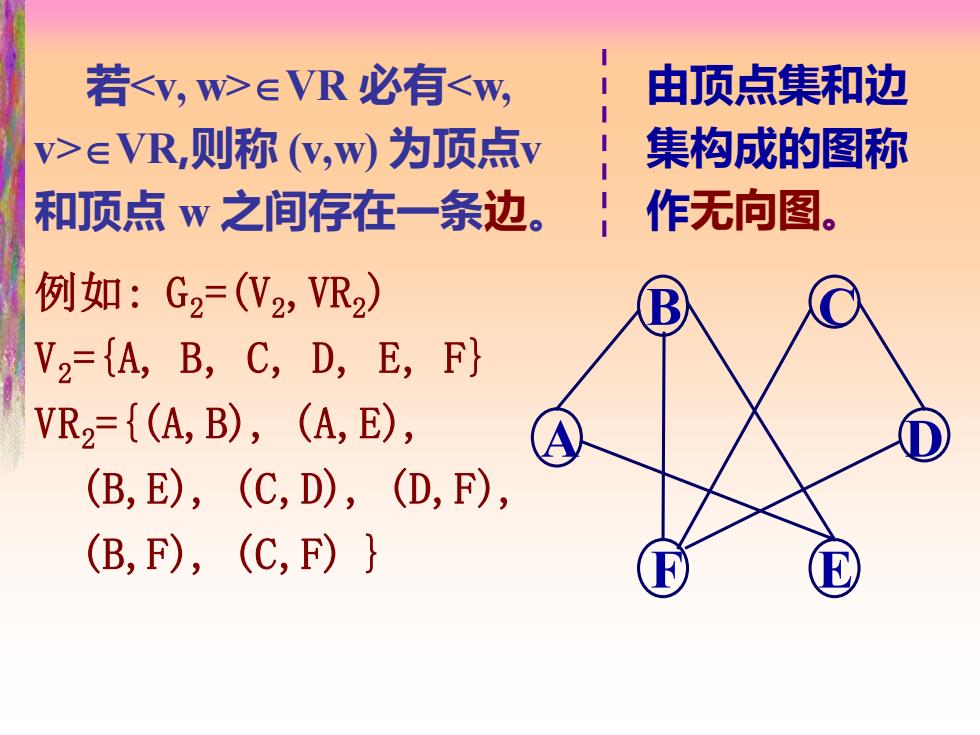
若eVR必有∈VR,则称(W,w为顶点v 集构成的图称 和顶点w之间存在一条边。} 作无向图。 例如:G2=(V2,VR2) V2=A,B,C,D,E,F} VR2={(A,B),(A,E), (B,E),(C,D),(D,F), (B,F),(C,F)}
若VR 必有VR,则称 (v,w) 为顶点v 和顶点 w 之间存在一条边。 B C A D F E 由顶点集和边 集构成的图称 作无向图。 例如: G2=(V2,VR2) V2={A, B, C, D, E, F} VR2={(A,B), (A,E), (B,E), (C,D), (D,F), (B,F), (C,F) }
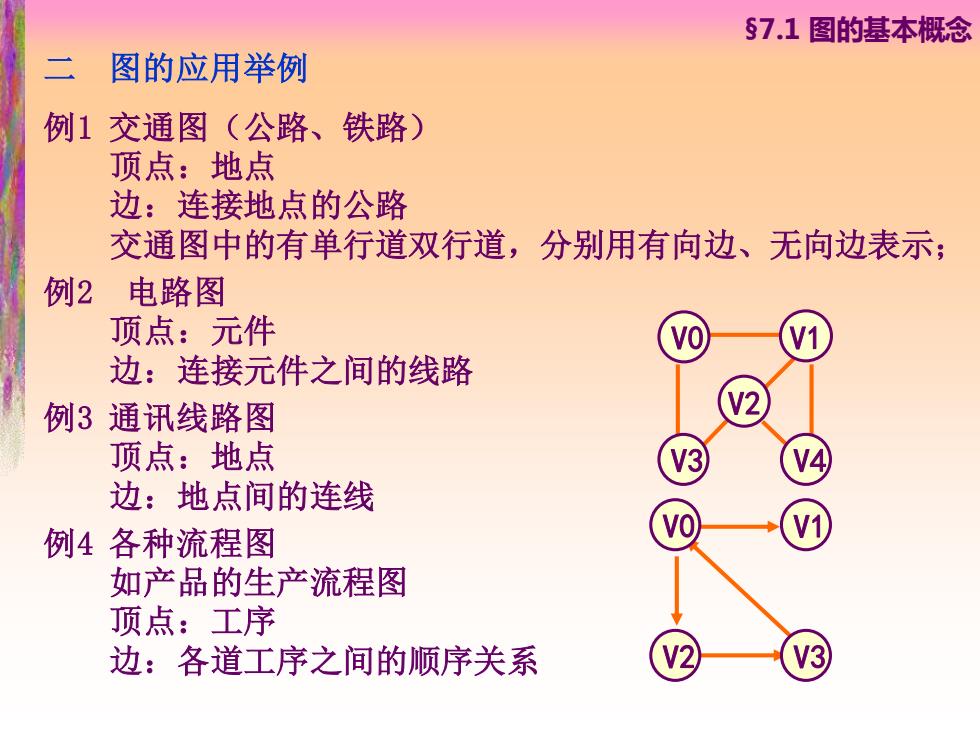
§7.1图的基本概念 二 图的应用举例 例1交通图(公路、铁路) 顶点:地点 边:连接地点的公路 交通图中的有单行道双行道,分别用有向边、无向边表示; 例2 电路图 顶点:元件 边:连接元件之间的线路 例3通讯线路图 顶点:地点 V3 边:地点间的连线 例4各种流程图 如产品的生产流程图 顶点:工序 边:各道工序之间的顺序关系 V3
二 图的应用举例 例1 交通图(公路、铁路) 顶点:地点 边:连接地点的公路 交通图中的有单行道双行道,分别用有向边、无向边表示; 例2 电路图 顶点:元件 边:连接元件之间的线路 例3 通讯线路图 顶点:地点 边:地点间的连线 例4 各种流程图 如产品的生产流程图 顶点:工序 边:各道工序之间的顺序关系 §7.1 图的基本概念 V0 V3 V4 V1 V2 V0 V1 V2 V3

名词和术语 网、子图→ 完全图、稀疏图、稠密图→ 邻接点、度、入度、出度 路径、路径长度、简单路径、简单回路→ 连通图、连通分量、 强连通图、强连通分量 生成树、生成森林 回
网、子图 完全图、稀疏图、稠密图 邻接点、度、入度、出度 路径、路径长度、简单路径、简单回路 连通图、连通分量、 强连通图、强连通分量 生成树、生成森林 名词和术语