山东第一医科大学（泰山医学院）：《数据结构》课程教学资源（PPT课件）第5章 数组和广义表

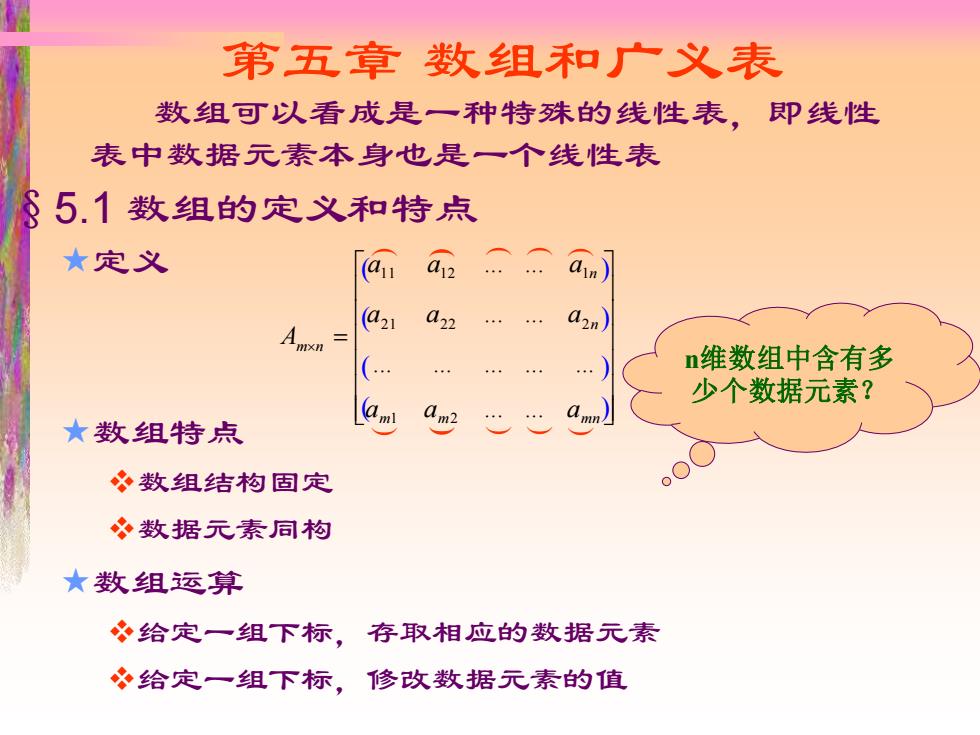
第五章数组和广义表 数组可以看成是一种特殊的线性表，即线性 表中数据元素本身也是一个线性表 §5.1数组的定义和特点 ★定义 a au) (a21 a22 (… n维数组中含有多 少个数据元素？ ★数组特点 数组结构固定 ?数据元素同构 ★数组运算 冬给定一组下标，存取相应的数据元素 必给定一组下标，修改数据元素的值

第五章 数组和广义表 数组可以看成是一种特殊的线性表，即线性 表中数据元素本身也是一个线性表 §5.1 数组的定义和特点 定义                  = m m mn n n m n a a a a a a a a a A ... ... ... ... ... ... ... ... ... ... ... 1 2 21 22 2 11 12 1 数组特点 ❖数组结构固定 ❖数据元素同构 数组运算 ❖给定一组下标，存取相应的数据元素 ❖给定一组下标，修改数据元素的值 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) n维数组中含有多 少个数据元素？

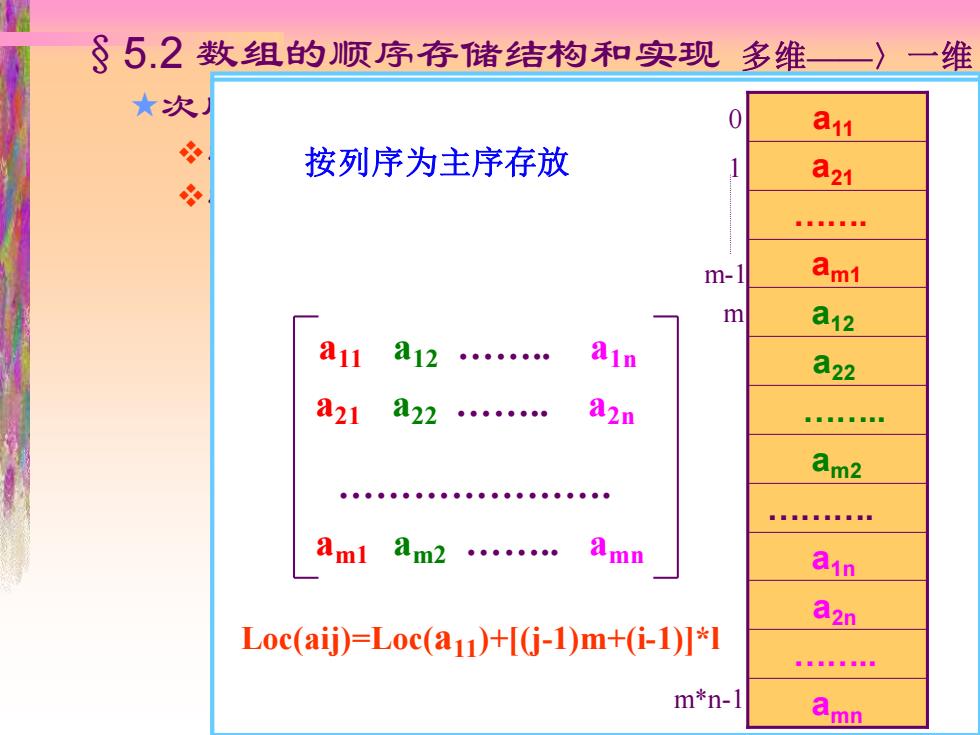
§5.2数组的顺序存储结构和实现多维一)一维 ★次 a11 按列序为主序存放 a21 8量■级银■数 m- am1 m a12 11 a12 a22 a21 222 ●●●9●●●。 82n 量：道道。量日业 am2 ●●。。9●9●●e●。●。。●●。。。●o Aml am2… Amn ain a2n Loc(aij)=Loc(a11)+[(j-1)m+(i-1)]*I g8。g8年 m*n-】 a

§5.2 数组的顺序存储结构和实现 次序约定 ❖以行序为主序 ❖以列序为主序 a11 a12 …….. a1n a21 a22 …….. a2n am1 am2 …….. amn …………………. Loc( aij)=Loc(a11)+[(i-1)n+(j-1)]*l 按行序为主序存放 amn …….. am2 am1 ………. a2n …….. a22 a21 a1n ……. a12 0 a11 1 n-1 m*n-1 n 按列序为主序存放 0 1 m-1 m*n-1 m amn …….. a2n a1n ………. am2 …….. a22 a12 am1 ……. a21 a11 a11 a12 …….. a1n a21 a22 …….. a2n am1 am2 …….. amn …………………. Loc(aij)=Loc(a11)+[(j-1)m+(i-1)]*l 多维——〉一维

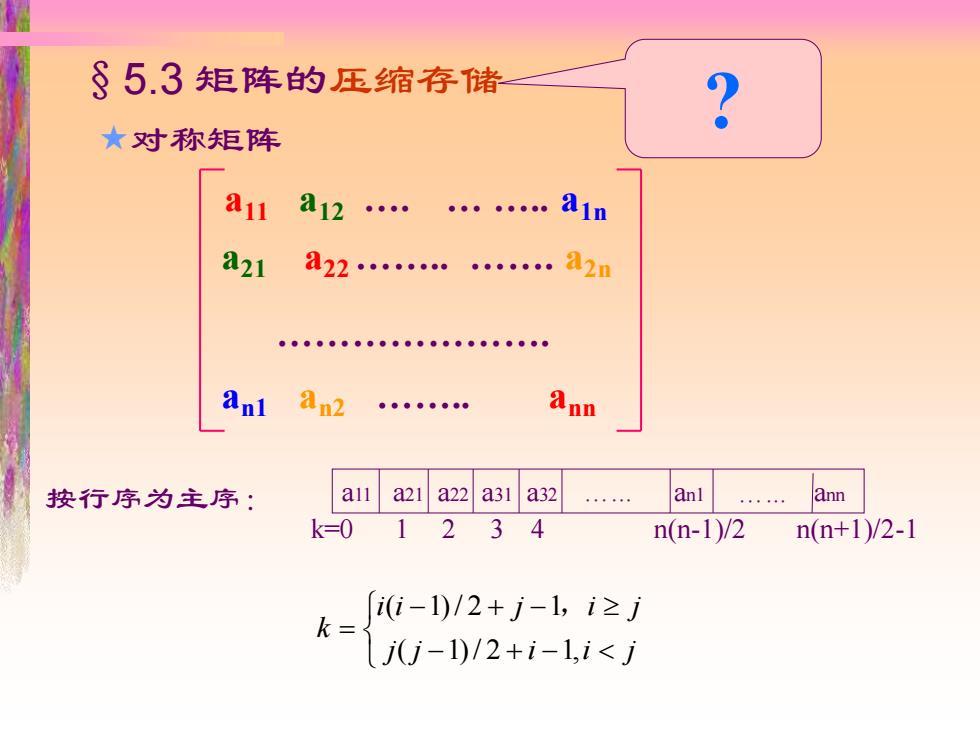
§5.3矩阵的压缩存储 ★对称矩阵 a11 a12. ●。。0●0 ain 221 a22……8a2n Anl an2 ●●●●●●●● Ann 按行序为主序： alla21a22a31a32 anl ann k=0 1234 n(n-1)/2 n(n+1)/2-1 [ii-1)/2+j-1,i≥j k= j(U-1)/2+i-1,i<j

§5.3 矩阵的压缩存储    − + −  − + −  = j j i i j i i j i j k ( 1)/ 2 1, ( 1)/ 2 1， a11 a12 …. … ….. a1n a21 a22…….. ……. a2n an1 an2 …….. ann …………………. a11 a21 a22 a31 a32 …... an1 …... ann k=0 1 2 3 4 n(n-1)/2 n(n+1)/2-1 按行序为主序： ? 对称矩阵

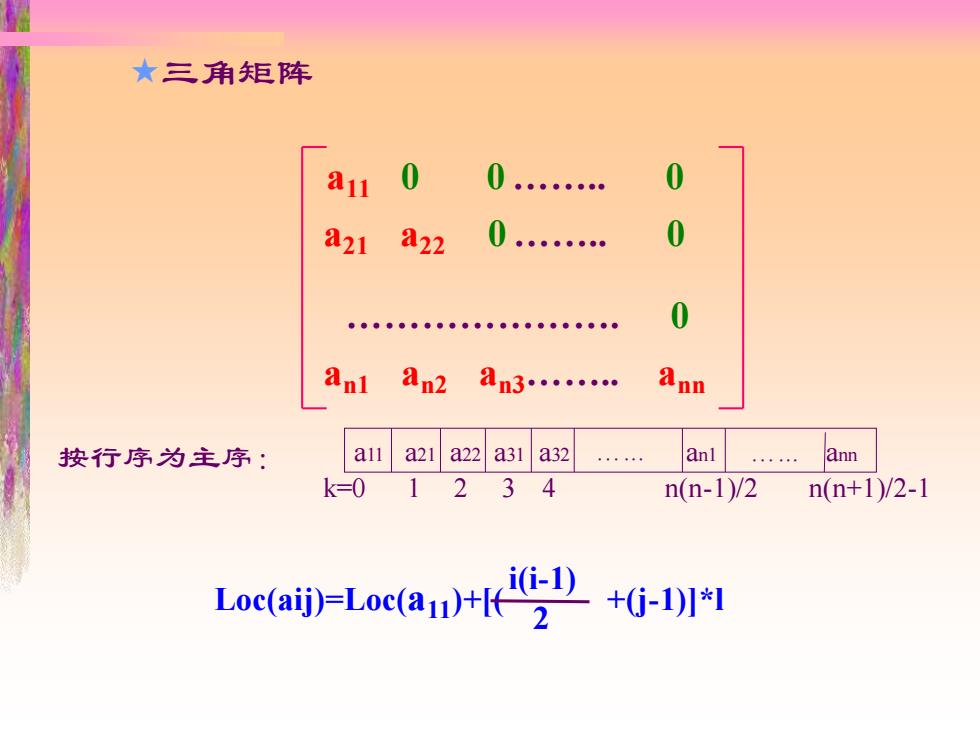
★三角矩阵 a11 0 0… a21 a22 0.… ●●●●●●●。●。●●●●●●●。●●●。 0 Anl an2 an3… 8n0 按行序为主序： all a21a22a31a32 anl ann k=0 1234 n(n-1)/2 n(n+1)/2-1 Loc(ai--Loc(a)+KD+-1内

三角矩阵 a11 0 0 …….. 0 a21 a22 0 …….. 0 an1 an2 an3…….. ann …………………. 0 Loc(aij)=Loc(a11)+[( +(j-1)]*l i(i-1) 2 a11 a21 a22 a31 a32 …... an1 …... ann k=0 1 2 3 4 n(n-1)/2 n(n+1)/2-1 按行序为主序：

5.3矩阵的压缩存储 ★稀疏矩阵 冬定义：非零元较零元少，且分布没有一定规律的矩阵 必压缩存储原则：只存矩阵的行列维数和每个非零元的 行列下标及其值 如何进行稀疏矩 0 12 9 阵的压缩存储？ 0 0 0 0 -3 00 0° 014 0 M= 0 024 0 00 0 0 180 0 0 0 0 表示非零元的 1500 -700 0J6x1 三元组 M由{1,2,12)，(1,3,9)，(3,1，-3)，(3,6,14)，(4,3,24) (5,2,18),(6,1,15),(6,4,-7}和矩阵维数(6,7)唯一确定

15 0 0 7 0 0 0 6 7 0 18 0 0 0 0 0 0 0 24 0 0 0 0 3 0 0 0 0 14 0 0 0 0 0 0 0 0 0 12 9 0 0 0 0                      − − M = M由{(1,2,12), (1,3,9), (3,1,-3), (3,6,14), (4,3,24), (5,2,18), (6,1,15), (6,4,-7) } 和矩阵维数（6,7）唯一确定 5.3 矩阵的压缩存储 稀疏矩阵 ❖定义：非零元较零元少，且分布没有一定规律的矩阵 表示非零元的 三元组 ❖压缩存储原则：只存矩阵的行列维数和每个非零元的 行列下标及其值 如何进行稀疏矩 阵的压缩存储？

稀疏矩阵的压缩存储方法 三元组顺序表 行逻辑连接的倾序表 十字链表

❖稀疏矩阵的压缩存储方法 三元组顺序表 行逻辑链接的顺序表 十字链表

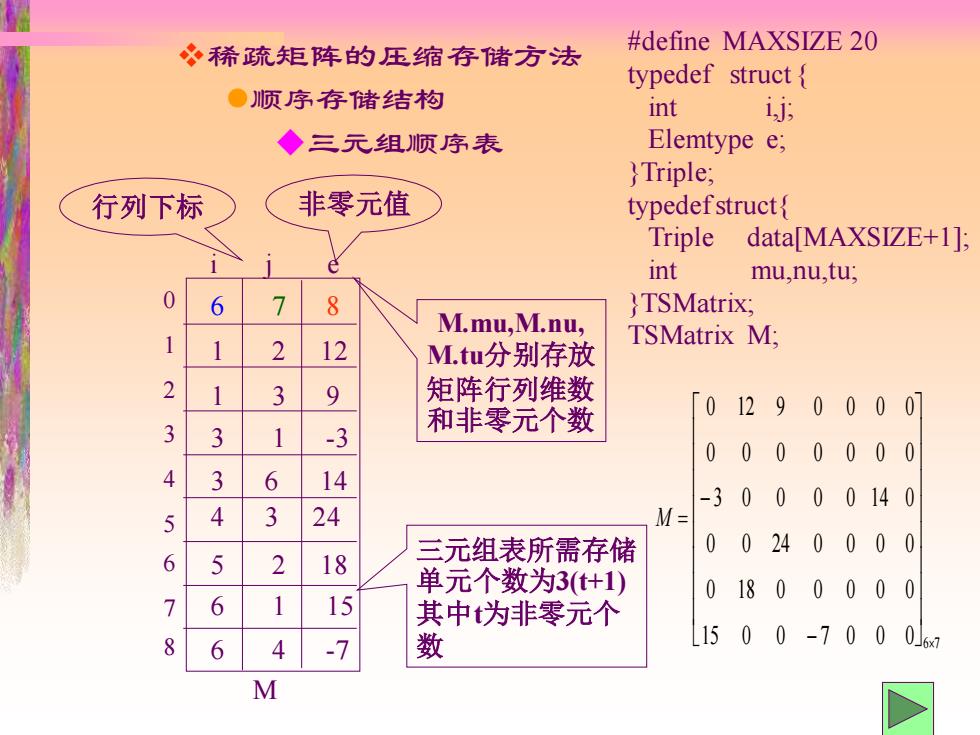
稀疏矩阵的压缩存储方法 #define MAXSIZE 20 typedef struct{ ●顺序存储结构 int ij; ◆三元组顺序表 Elemtype e; }Triple; 行列下标 非零元值 typedefstruct Triple data[MAXSIZE+1]; int mu,nu,tu; 0 6 8 }TSMatrix; M.mu,M.nu, 2 12 TSMatrix M; M.tu分别存放 2 3 矩阵行列维数 和非零元个数 0 129 0000 3 3 -3 0000000 4 3 6 14 -30000140 5 4 3 24 M= 三元组表所需存储 00240000 6 5 2 18 单元个数为3(t+1) 15 01800000 7 6 其中为非零元个 1500-700 8 6 4 -7 数 06 M

❖稀疏矩阵的压缩存储方法 ⚫顺序存储结构 ◆三元组顺序表 #define MAXSIZE 20 typedef struct { int i,j; Elemtype e; }Triple; typedef struct{ Triple data[MAXSIZE+1]; int mu,nu,tu; }TSMatrix; TSMatrix M; 三元组表所需存储 单元个数为3(t+1) 其中t为非零元个 数 6 7 8 1 2 12 1 3 9 3 1 -3 3 6 14 4 3 24 5 2 18 6 1 15 6 4 -7 M i j e 0 1 2 3 4 5 6 7 8 M.mu,M.nu, M.tu分别存放 矩阵行列维数 和非零元个数 行列下标 非零元值 15 0 0 7 0 0 0 6 7 0 18 0 0 0 0 0 0 0 24 0 0 0 0 3 0 0 0 0 14 0 0 0 0 0 0 0 0 0 12 9 0 0 0 0                      − − M =

>求转置矩阵 女问题描述：已知一个稀疏矩阵的三元组表， 求该矩阵转置矩阵的三元组表 问题分析 常规的二维数组表示时转置的算法： for(col=1;col<=nu;++col) for(row=1;row<-mu;++row) T[col][row]=M[row][col]: T(n)-O(muxnu)

问题描述：已知一个稀疏矩阵的三元组表， 求该矩阵转置矩阵的三元组表 问题分析 常规的二维数组表示时转置的算法： for(col=1;col<=nu;++col) for(row=1;row<=mu;++row) T[col][row]=M[row][col]; T(n)=O(munu) ➢求转置矩阵

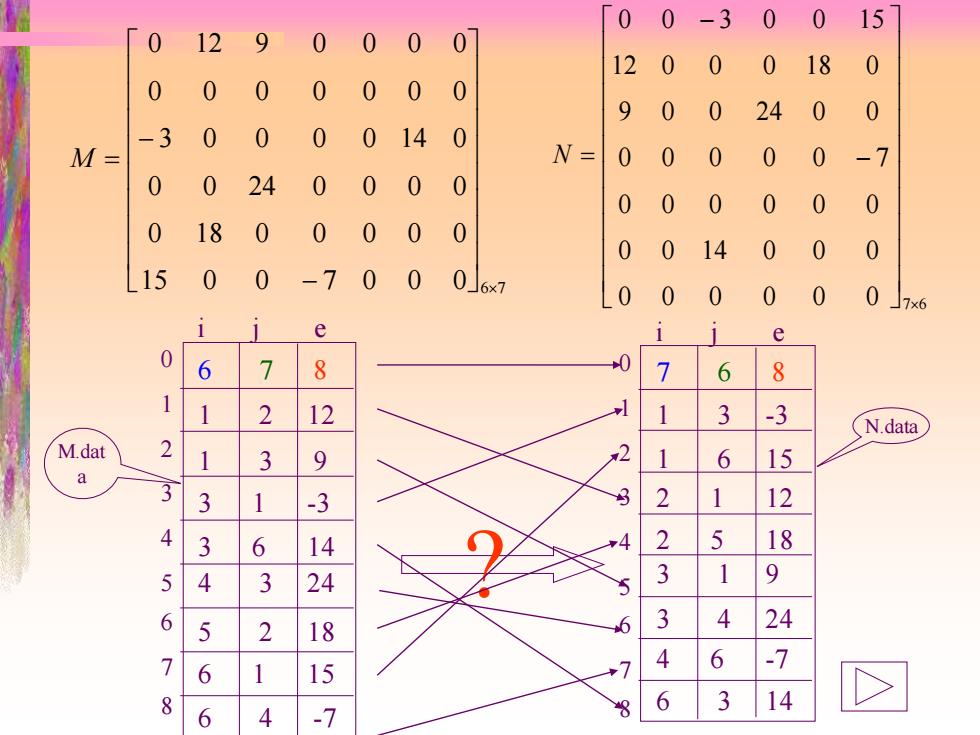
0 0-3 0 0 15 0 12 0 0 0 120 0 0 18 0 0 0 0 0 0 0 0 9 0 0 24 0 0 -3 0 0 0 014 0 M= N= 0 0 0 0 0 -7 0 0 24 0 0 0 0 0 0 0 0 0 0 0 18 0 0 0 0 0 0 0 14 0 0 0 15 0 0 -7 0 0 0」6x7 0 0 0 0 0 0 ☐7×6 1 e 0 6 7 8 7 6 8 1 1 2 12 1 3 -3 N.data M.dat 2 1 3 9 2 1 6 15 a 3 -3 3 2 12 4 3 6 14 2 5 18 5 4 3 24 3 1 9 6 5 4 2 18 24 7 4 6 15 -7 6 8 6 3 14 6 4 -7

15 0 0 7 0 0 0 6 7 0 18 0 0 0 0 0 0 0 24 0 0 0 0 3 0 0 0 0 14 0 0 0 0 0 0 0 0 0 12 9 0 0 0 0    − − M = 0 0 0 0 0 0 7 6 0 0 14 0 0 0 0 0 0 0 0 0 0 0 0 0 0 7 9 0 0 24 0 0 12 0 0 0 18 0 0 0 3 0 0 15    − − N = 6 7 8 1 2 12 1 3 9 3 1 -3 3 6 14 4 3 24 5 2 18 6 1 15 6 4 -7 i j e 012345678 M.dat a i j e 7 6 8 1 3 -3 1 6 15 2 1 12 2 5 18 3 1 9 3 4 24 4 6 -7 6 3 14 012345678 N.data ?

0 129 000 0 0 3 0 15 稀疏矩阵三元组转置算法 0 00 0000 0 0 0 18 -30 0 0014 0 9 0 0 24 0 00 M 0 024 000 T三 0 0 0 0 0 解决思路：只要做到 0 0 0 0 0 180 000 0 0 0 14 0 00 ①将矩阵行、列维数互换 15 00-700 0 0 0 0 0 0 ②将每个三元组中的i和j相互调换 ③重排三元组次序，使T.data中元素以T的行(M的列)为主序 方法一：按M的列序转置 即按T.data中三元组次序依次在M.data中找到相应的三元组 进行转置。为找到M中每一列所有非零元素，需对其三元组表 M.data从第一行起扫描一遍。由于M.data中以M行序为主序， 所以由此得到的恰是T.data中应有的顺序 卒算法分析：T()=O(M的列数n×非零元个数t) 若t与mxn同数量级，则T(nm)=O(m×n2)

解决思路：只要做到 将矩阵行、列维数互换 将每个三元组中的i和j相互调换 重排三元组次序，使T.data中元素以T的行(M的列)为主序 方法一：按M的列序转置 即按T.data中三元组次序依次在M.data中找到相应的三元组 进行转置。为找到M中每一列所有非零元素，需对其三元组表 M.data从第一行起扫描一遍。由于M.data中以M行序为主序, 所以由此得到的恰是T.data中应有的顺序 算法分析：T(n)=O(M的列数n非零元个数t) 若 t 与mn同数量级，则 ( ) ( ) 2 T n = O m n 稀疏矩阵三元组转置算法 15 0 0 7 0 0 0 6 7 0 18 0 0 0 0 0 0 0 24 0 0 0 0 3 0 0 0 0 14 0 0 0 0 0 0 0 0 0 12 9 0 0 0 0                      − − M = − 7 0 0 0 0 0 0 0 0 14 0 0 0 0 0 0 0 0 0 0 0 0 0 0 9 0 0 24 0 0 12 0 0 0 18 0 0 0 3 0 0 15 7×6 T ＝ −