第三章栈和队列 栈和队列是两种特殊的线性表,是操作受限的线 性表,称限定性DS §3.1栈(stack) ★栈的定义和特点 定义:限定仅在表尾进行插入或删除操作的线性表, 表尾一栈顶,表头一栈底,不含元素的空表称空栈 特点:先进后出(FLO)或后进先出(LFO) 进栈 出栈 顶 An 栈s=(al,a2,.…,an a2 栈底 a1
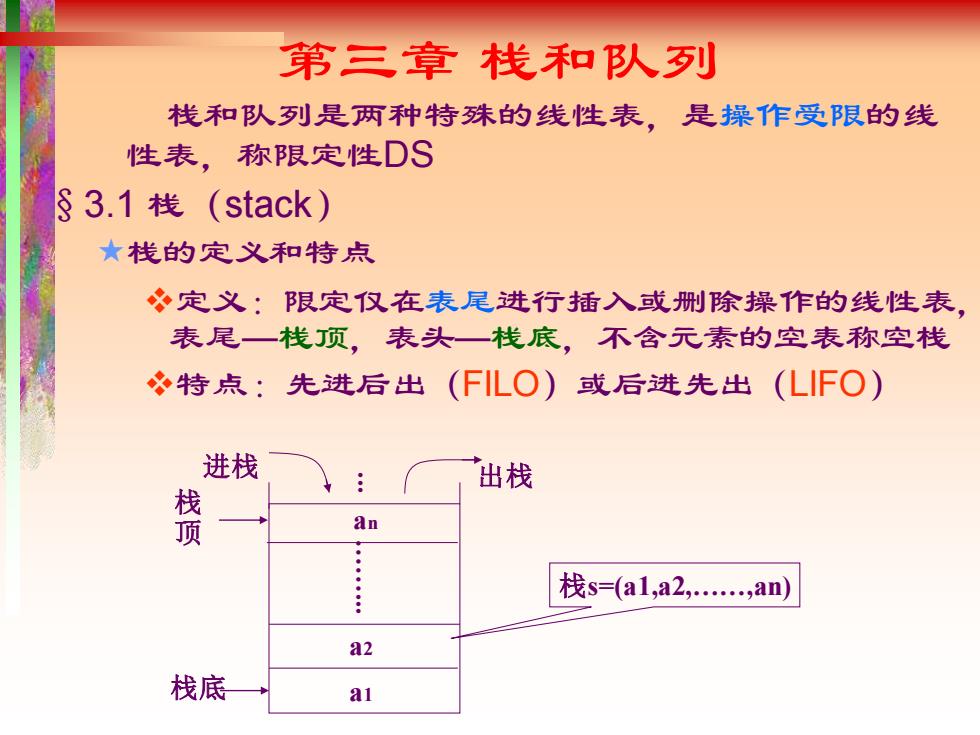
第三章 栈和队列 栈和队列是两种特殊的线性表,是操作受限的线 性表,称限定性DS §3.1 栈(stack) 栈的定义和特点 ❖定义:限定仅在表尾进行插入或删除操作的线性表, 表尾—栈顶,表头—栈底,不含元素的空表称空栈 ❖特点:先进后出(FILO)或后进先出(LIFO) an a1 a2……... 栈底 栈 顶 进栈 ... 出栈 栈s=(a1,a2,……,an)

饯的类型定义 ADT Stack{ 数据对象 D={a|a:∈ElemSet,.i=l,2,.,n,n≥0} 数据关系: RI={ai-,aED,i=2,...n 约定a,端为栈顶,a端为栈底。 基本操作: ADT Stack
栈的类型定义 ADT Stack { 数据对象: D={ ai | ai ∈ElemSet, i=1,2,...,n, n≥0 } 数据关系: R1={ | ai-1 , ai∈D, i=2,...,n } 约定an 端为栈顶,a1 端为栈底。 基本操作: } ADT Stack

InitStack(&S) DestroyStack(&S) StackLength(S) StackEmpty(s) GetTop(S,&e) ClearStack(&S) Push(&S,e) Pop(&S,&e) StackTravers(S,visitO)
InitStack(&S) DestroyStack(&S) ClearStack(&S) StackEmpty(s) StackLength(S) GetTop(S, &e) Push(&S, e) Pop(&S, &e) StackTravers(S, visit())
★栈的表示和实现 顺序栈 ●实现: 一维数组S[M我满 栈空 top top 5 F top top 4 top E top 4 3 top D top 3 3 2 top c top 2 top top B A top top=0 栈空 出栈 栈顶指针top,指向实际栈顶 设数组维数为M 后的空位置,初值为0 top=O,栈空,此时出栈,则下溢(underflow) top=M,栈满,此时入栈,则上溢(overflow)
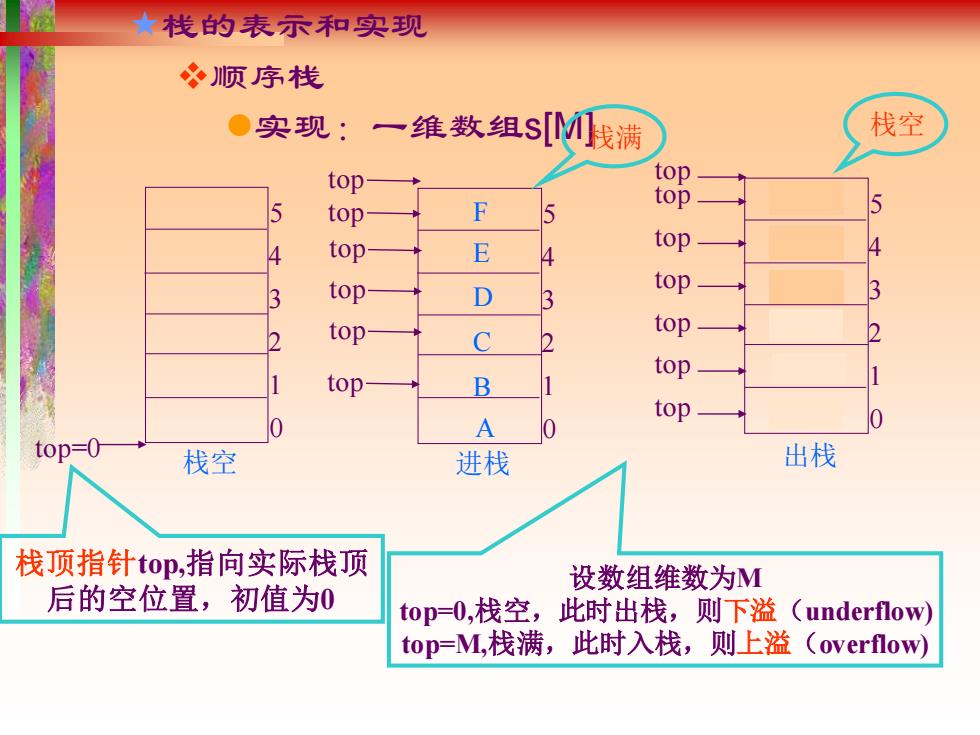
栈的表示和实现 ❖顺序栈 ⚫实现:一维数组s[M] top=0 1 2 3 4 5 0 栈空 栈顶指针top,指向实际栈顶 后的空位置,初值为0 top 1 2 3 4 5 0 进栈 A top 出栈 栈满 B C D E F 设数组维数为M top=0,栈空,此时出栈,则下溢(underflow) top=M,栈满,此时入栈,则上溢(overflow) top top top top top 1 2 3 4 5 A 0 B C D E top F top top top top top 栈空

栈的顺序存储表示: #define STACK INIT SIZE 100: #define STACKINCREMENT 10: Typedef struct{ SElemType *base; SElemType *top; int stacksize; SqStack; ●初始化算法 ●取栈项元素算法
⚫初始化算法 ⚫取栈项元素算法 栈的顺序存储表示: #define STACK_INIT_SIZE 100; #define STACKINCREMENT 10; Typedef struct { SElemType *base; SElemType *top; int stacksize; }SqStack;

构造空栈 Status InitStack(SqStack &S){ /构造一个空栈$ S.base=(SElemType *)malloc (STACK INIT SIZE sizeof(SElemType)); if(IS.base)exit(OVERFLOW);H/存储分配失败 S.top-S.base; S.stacksize=STACK INIT SIZE: return OK; //InitStack
Status InitStack(SqStack &S) { // 构造一个空栈S S.base=(SElemType *) malloc (STACK_INIT_SIZE * sizeof(SElemType)); if (!S.base) exit (OVERFLOW);//存储分配失败 S.top=S.base; S.stacksize=STACK_INIT_SIZE; return OK; }//InitStack 构造空栈

Stack GetTop(SqStack S,SElemType &e){ /若栈不空,则用返回S的栈顶元素,并返回OK, /否则返回ERROR; if(S.top-=S.base)return ERROR; e-*(S.top-1); return OK: //GetTop
Stack GetTop (SqStack S,SElemType &e) { //若栈不空,则用e返回S的栈顶元素,并返回OK, //否则返回ERROR; if (S.top==S.base) return ERROR; e=*(S.top-1); return OK; }//GetTop
●入栈算法 ●出栈算法 ●在一个程序中同时使用两个栈 M-1 栈1底 栈1顶 栈2顶 栈2底
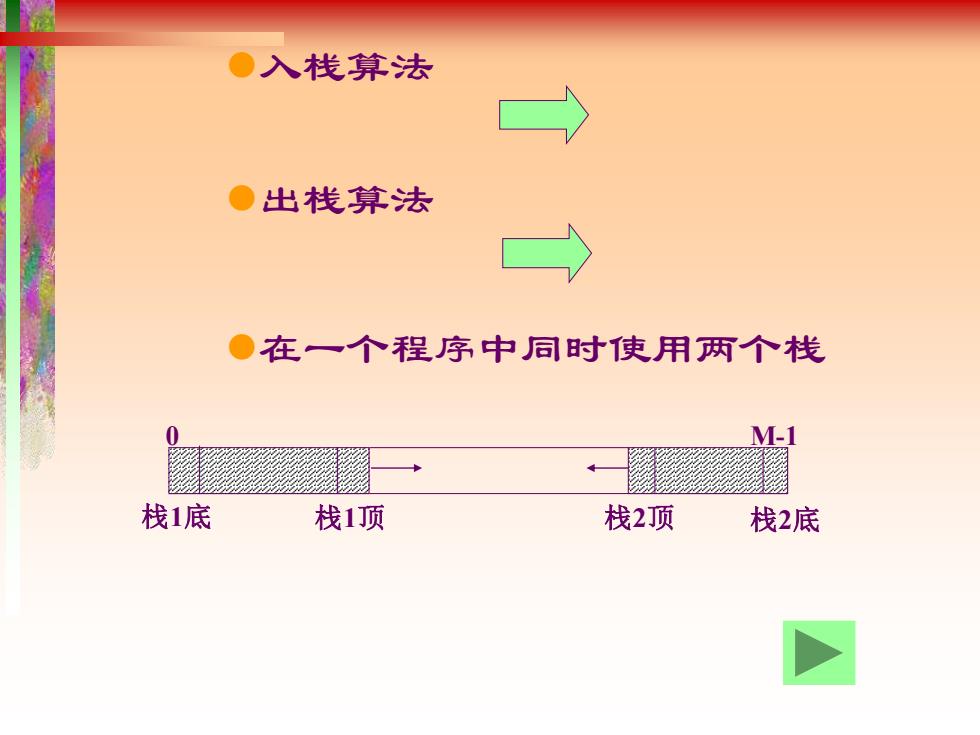
⚫入栈算法 0 M-1 栈1底 栈1顶 栈2顶 栈2底 ⚫出栈算法 ⚫在一个程序中同时使用两个栈

入栈 Status Push(SqStack &S,SElemType e){ /插入元素e为新的栈顶元素 if(S.top-S.base>=S.stacksize){ S.base=(ElemType *)realloc (S.base, (S.stacksize+STACKINCREMENT)*sizeof(ElemType));; if(IS.base)exit (OVERFLOW): S.top-S.base+S.stacksize; S.stacksize+=STACKINCREMENT: } *S.top++-e; return OK; //Push
Status Push(SqStack &S,SElemType e) { //插入元素e为新的栈顶元素 if (S.top-S.base>=S.stacksize) { S.base=(ElemType *) realloc (S.base, (S.stacksize+STACKINCREMENT)* sizeof(ElemType));; if (!S.base) exit (OVERFLOW); S.top=S.base+S.stacksize; S.stacksize+=STACKINCREMENT; } *S.top++=e; return OK; }//Push 入栈

int push(int s[],int x,int top) if(top=-M) printf("overflow"): return(-M): s[top]-x; return(++top); d
int push(int s[],int x,int top) { if(top==M) { printf("overflow"); return(-M); } s[top]=x; return(++top); }