
第十章排序 ★排序定义一将一个数据元素(或记录)的任意序列, 重新排列成一个按关键字有序的序列叫~ ★排序分类 按待排序记录所在位置 ●内部排序:待排序记录存放在内存 ●外部排序:排序过程中需对外存进行访问的排序 按排序依据原则 ●插入排序:直接插入排序、折半插入排序、希尔 排序 ●交换排序:冒泡排序、快速排序 ●选择排序:简单选择排序、堆排序 ●归并排序:2-路归并排序 ●基数排序
第十章 排序 排序定义——将一个数据元素(或记录)的任意序列, 重新排列成一个按关键字有序的序列叫~ 排序分类 ❖按待排序记录所在位置 ⚫内部排序:待排序记录存放在内存 ⚫外部排序:排序过程中需对外存进行访问的排序 ❖按排序依据原则 ⚫插入排序:直接插入排序、折半插入排序、希尔 排序 ⚫交换排序:冒泡排序、快速排序 ⚫选择排序:简单选择排序、堆排序 ⚫归并排序:2-路归并排序 ⚫基数排序

必按排序所需工作量 ●简单的排序方法:T(n)=○n) ●先进的排序方法:T(n)=O(logn) ●基数排序:T(n)=O(d.n) ★排序基本操作 比较两个关键字大小 将记录从一个位置移动到另一个位置
❖按排序所需工作量 ⚫简单的排序方法:T(n)=O(n²) ⚫先进的排序方法:T(n)=O(logn) ⚫ 基数排序:T(n)=O(d.n) 排序基本操作 ❖比较两个关键字大小 ❖将记录从一个位置移动到另一个位置

§10.2插入排序 ★直接插入排序 排序过程:整个排序过程为门-1趟插入, 即先将序列中第1个记录看成是一个有序 子序列,然后从第2个记录开始,逐个进 行插入,直至整个序列有序
§10.2 插入排序 直接插入排序 ❖排序过程:整个排序过程为n-1趟插入, 即先将序列中第1个记录看成是一个有序 子序列,然后从第2个记录开始,逐个进 行插入,直至整个序列有序

例 1 (49386597761327 i=238(3849)65 97761327 i=365(3849 65)97761327 i=497(38496597) 761327 i=576(3849657697)1327 =613(133849657697)27 i=727(13273849657697 排序结果:(13273849657697)
例 49 38 65 97 76 13 27 i=2 38 (38 49) 65 97 76 13 27 i=3 65 (38 49 65) 97 76 13 27 i=4 97 (38 49 65 97) 76 13 27 i=5 76 (38 49 65 76 97) 13 27 i=6 13 (13 38 49 65 76 97) 27 i=1 ( ) i=7 (13 38 49 65 76 97) 27 27 j j j j j j 27 38 49 65 76 97 排序结果:(13 27 38 49 65 76 97)

$算法评价 ●时间复杂度 ◆若待排序记录按关键字从小到大排列(正序) 女关键字比较次数: 21=n-1 海记录移动次数: ◆若待排序记录按关键字从大到小排列(逆序) 意关键字比较次数:=+2n一 2 攻记录移动次数: G+1D)=n+4n-) i=2 2 ◆若待排序记录是随机的,取平均值 n 章关键字比较次数: 4 记录移动次数: T(n)=0(n2) ●空间复杂度:S(n)=0(1)
❖算法评价 ⚫时间复杂度 ◆若待排序记录按关键字从小到大排列(正序) 关键字比较次数: 1 1 2 = − = n n i 记录移动次数: ◆若待排序记录按关键字从大到小排列(逆序) 关键字比较次数: 2 ( 2)( 1) 2 + − = = n n i n i 记录移动次数: 2 ( 4)( 1) ( 1) 2 + − + = = n n i n i ◆若待排序记录是随机的,取平均值 关键字比较次数: 4 2 n 记录移动次数: 4 2 n T(n)=O(n²) ⚫空间复杂度:S(n)=O(1)

★折半插入排序 必排序过程:用折半查找方法确定插入位置的 排序叫~ 例 -1 (30)1370853942620 i=213 (13 30)70853942620 i=76 (6 13 30 39 42 70 85)20 i=8 20 1330 39 427085)20 m h i=820 ( B309 4270 85)20 h i=8 20 (6 13 39 42 70 85)20 i=8 20 (6 30 39 4270 85)20 h i=820 (6 13 203039427085)
折半插入排序 ❖排序过程:用折半查找方法确定插入位置的 排序叫~ 例 i=1 (30) 13 70 85 39 42 6 20 i=2 13 (13 30) 70 85 39 42 6 20 i=7 6 (6 13 30 39 42 70 85 ) 20 …... i=8 20 (6 13 30 39 42 70 85 ) 20 l m h i=8 20 (6 13 30 39 42 70 85 ) 20 l m h i=8 20 (6 13 30 39 42 70 85 ) 20 l mh i=8 20 (6 13 30 39 42 70 85 ) 20 h l i=8 20 (6 13 20 30 39 42 70 85 )

★希尔排序(缩小增量法) 排序过程:先取一个正整数d1<n,把所 有相隔d1的记录放一组,组内进行直接 插入排序;然后取d2<d1,重复上述分 组和排序操作;直至di=1,即所有记录 放进一个组中排序为止
希尔排序(缩小增量法) ❖排序过程:先取一个正整数d1<n,把所 有相隔d1的记录放一组,组内进行直接 插入排序;然后取d2<d1,重复上述分 组和排序操作;直至di=1,即所有记录 放进一个组中排序为止

例初始:4938659776132748554 取d1=5 一趟分组:493865977613 27 48554 一趟排序:1327485544938659776 取d2=3 二趟分组:13 27485544938659776 二趟排序:1344838274955659776 取d3=1 三趟分组:1327485544938 659776 三趟排序:4132738484955 657697
取d3=1 三趟分组:13 27 48 55 4 49 38 65 97 76 三趟排序:4 13 27 38 48 49 55 65 76 97 例 初始: 49 38 65 97 76 13 27 48 55 4 一趟排序:13 27 48 55 4 49 38 65 97 76 二趟排序:13 4 48 38 27 49 55 65 97 76 取d1=5 一趟分组:49 38 65 97 76 13 27 48 55 4 取d2=3 二趟分组:13 27 48 55 4 49 38 65 97 76
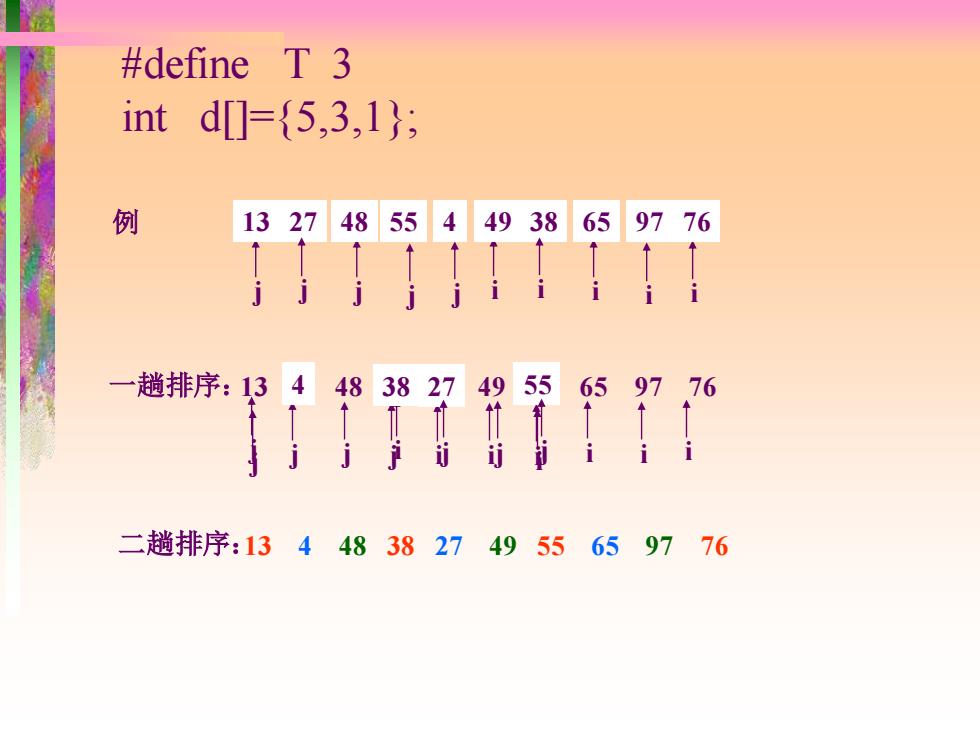
#define T 3 int d0={5,3,1}; 例 1327485544938659776 }! 一趟排序:1344838274955659776 I0f:1 二趟排序:1344838274955659776
例 49 38 65 97 76 13 27 48 55 4 #define T 3 int d[]={5,3,1}; j i 13 27 49 38 一趟排序:13 27 48 55 4 49 38 65 97 76 j j i i 4 27 j j i i 55 j i 38 j j j i i i 二趟排序:13 4 48 38 27 49 55 65 97 76 j j i i 48 65 j i 55 97 j i 4 76

必希尔排序特点 ●子序列的构成不是简单的“逐段分割”, 而是将相隔某个增量的记录组成一个子序 列 ●希尔排序可提高排序速度,因为 ◆分组后n值减小,n更小,而T(n)=0(n), 所以T()从总体上看是减小了 ◆关键字较小的记录跳跃式前移,在进行 最后一趟增量为1的插入排序时,序列已 基本有序 ●增量序列取法 ◆无除1以外的公因子 ◆最后一个增量值必须为1
❖希尔排序特点 ⚫子序列的构成不是简单的“逐段分割”, 而是将相隔某个增量的记录组成一个子序 列 ⚫希尔排序可提高排序速度,因为 ◆分组后n值减小,n²更小,而T(n)=O(n²), 所以T(n)从总体上看是减小了 ◆关键字较小的记录跳跃式前移,在进行 最后一趟增量为1的插入排序时,序列已 基本有序 ⚫增量序列取法 ◆无除1以外的公因子 ◆最后一个增量值必须为1