
数字图像处理 (Digital Image Processing) 第4章频率域滤波 2020年2月
数字图像处理 (Digital Image Processing) 第4章 频率域滤波 2020年2月

频率域滤波 ·4.1背景 ·4.2基本概念 ·4.3取样和取样函数的傅立叶变换 ·4.4单变量的离散傅立叶变换 ·4.5两个变量的扩展 ·4.6二维离散傅立叶变换的一些性质 ·4.7频率域滤波基础 ·4.8频率域滤波器平滑图像 ·4.9频率域滤波器锐化图像 ·4.10选择性滤波
• 4.1 背景 • 4.2 基本概念 • 4.3 取样和取样函数的傅立叶变换 • 4.4 单变量的离散傅立叶变换 • 4.5 两个变量的扩展 • 4.6 二维离散傅立叶变换的一些性质 • 4.7 频率域滤波基础 • 4.8 频率域滤波器平滑图像 • 4.9 频率域滤波器锐化图像 • 4.10 选择性滤波 频率域滤波

§4.1傅立叶级数和变换简史 ●1807年完成《热的传播》,提出 任何连续周期信号可以由一组适 当的正弦曲线组合而成 M M Fourier, ∧AA ⊕ 1768~1830
Fourier, 1768 ~1830 1807年 完成《热的传播》,提出 任何连续周期信号可以由一组适 当的正弦曲线组合而成 §4.1 傅立叶级数和变换简史
§4.1傅立叶级数和变换简史 ●1807年完成《热的传播》,提出 任何连续周期信号可以由一组适 到9文有9酒前A日 当的正弦曲线组合而成 热的解析理论 halyucal Hoy mu ●1811年提交修改论文《热在固体 中的运动理论》,”获科学院大奖。 1傅立叶级数、傅立叶分析等理论均 Fourier, 由此创始。 1768~1830 色1822年,出版著名专著:热分析理论 0 TT+t 2T2T+t 3T3T+t Time
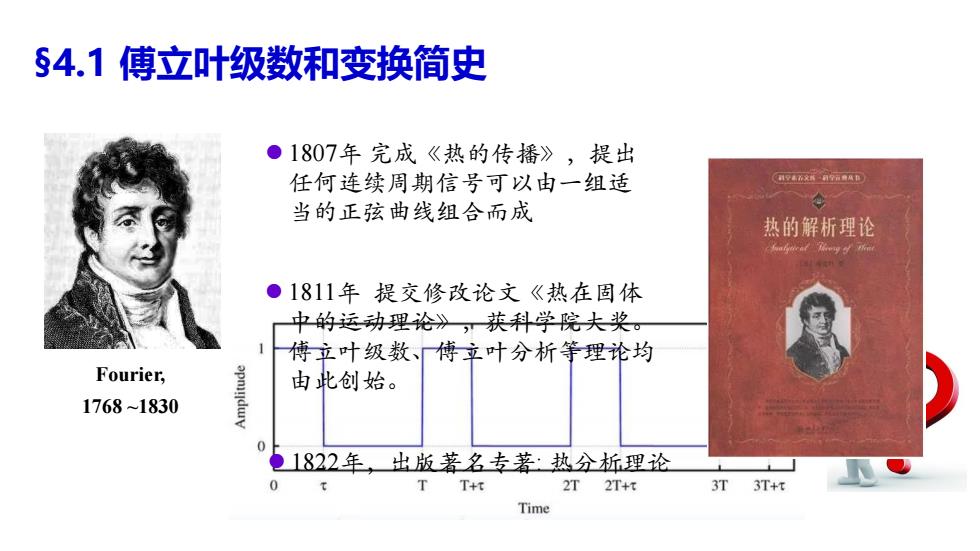
1807年 完成《热的传播》,提出 任何连续周期信号可以由一组适 当的正弦曲线组合而成 §4.1 傅立叶级数和变换简史 1811年 提交修改论文《热在固体 中的运动理论》,获科学院大奖。 傅立叶级数、傅立叶分析等理论均 由此创始。 1822年,出版著名专著: 热分析理论 Fourier, 1768 ~1830

§4.1傅立叶级数和变换简史 狄里赫利条件(1829年提出) ·在一个周期内连续或只有有限个第一类间断点(左极限=右极限) 。在一个周期内只有有限个极大值或极小值 ,周期函数的绝对值在一个周期内的积分存在
狄里赫利条件 (1829年提出) • 在一个周期内连续或只有有限个第一类间断点(左极限=右极限) • 在一个周期内只有有限个极大值或极小值 • 周期函数的绝对值在一个周期内的积分存在 §4.1 傅立叶级数和变换简史
§4.1傅立叶级数和变换简史 fx) 傅立叶级数 任何周期(周期为2)函数均可表示成不同频率的正弦和 T=2π 余弦函数的加权和: 00 2sinx ao nπx nπX f(x)= ancos +bnsin) n=1 3cosx an=f()cosdx (n=0.12. + 4sin2x + ba=f)sn2dkn=1.23) cos3x
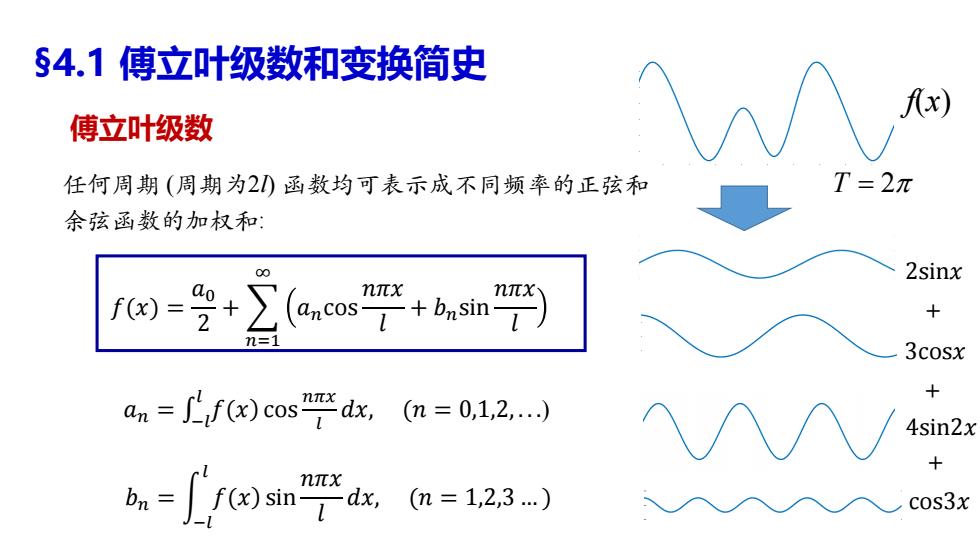
傅立叶级数 任何周期 (周期为2l) 函数均可表示成不同频率的正弦和 余弦函数的加权和: f(x) 𝑓(𝑥) = 𝑎0 2 + 𝑛=1 ∞ 𝑎𝑛cos 𝑛𝜋𝑥 𝑙 + 𝑏𝑛sin 𝑛𝜋𝑥 𝑙 ��− = �𝑎� 𝑙 𝑓(𝑥) cos 𝑛𝜋𝑥 𝑙 𝑑𝑥, (𝑛 = 0,1,2, . . .) 𝑏𝑛 = න −𝑙 𝑙 𝑓(𝑥) sin 𝑛𝜋𝑥 𝑙 𝑑𝑥, (𝑛 = 1,2,3 … ) 2sin𝑥 3cos𝑥 4sin2𝑥 cos3𝑥 + + + T 2 §4.1 傅立叶级数和变换简史

§4.1傅立叶级数和变换简史 傅立叶级数 一种直观解释:光的色散现象 红 橙 白色 黄十 绿 蓝靛紫 白色 =∑an Sin(nx)
一种直观解释:光的色散现象 §4.1 傅立叶级数和变换简史 傅立叶级数
§4.1傅立叶级数和变换简史 傅立叶级数 -2T 00 a 2+∑ nπx nπx f(x)= ancos+bnsin) m=1
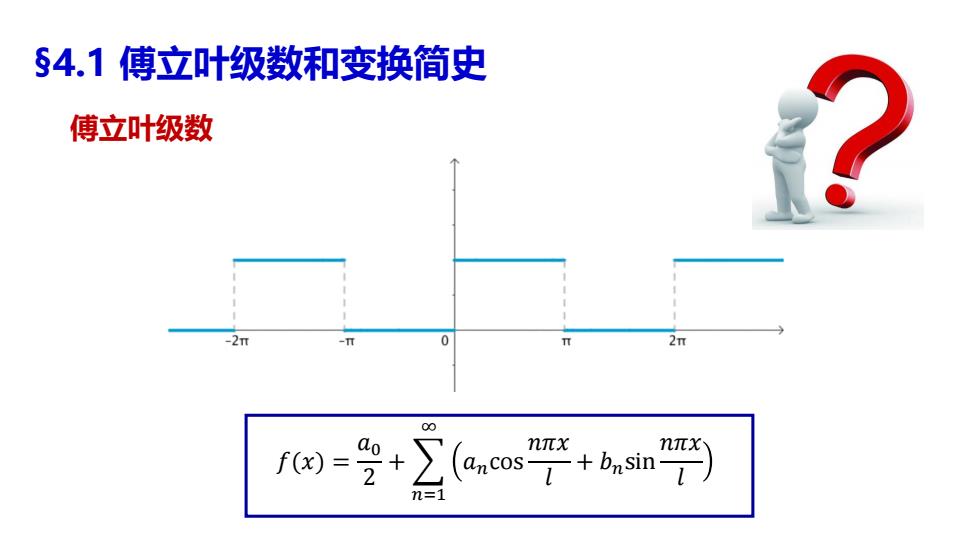
𝑓(𝑥) = 𝑎0 2 + 𝑛=1 ∞ 𝑎𝑛cos 𝑛𝜋𝑥 𝑙 + 𝑏𝑛sin 𝑛𝜋𝑥 𝑙 §4.1 傅立叶级数和变换简史 傅立叶级数
§4.1傅立叶级数和变换简史 傅立叶级数 -2 0 21 4 00 fx)≈1+4sin(x) πx nπX f(x)= ao 2 ancos- +bnsin-1) n=1
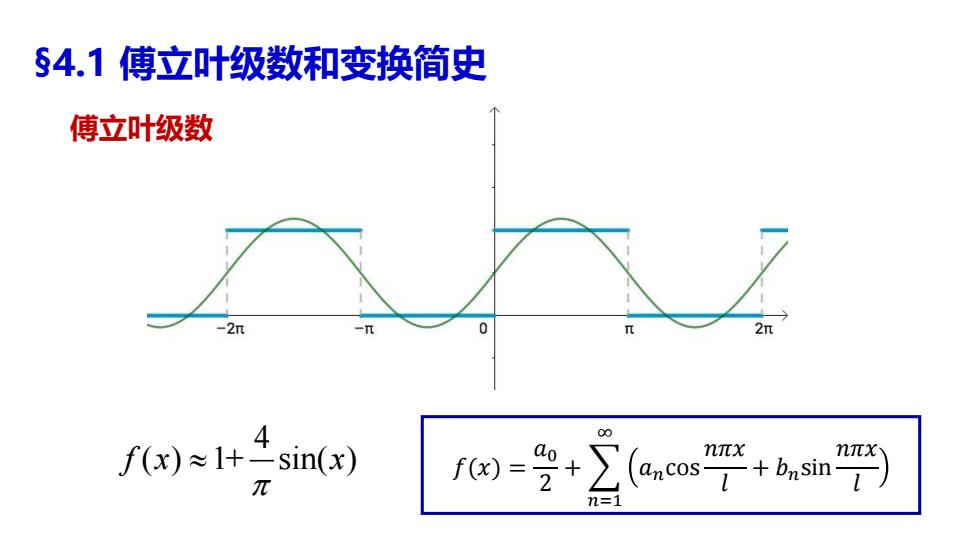
§4.1 傅立叶级数和变换简史 𝑓(𝑥) = 𝑎0 2 + 𝑛=1 ∞ 𝑎𝑛cos 𝑛𝜋𝑥 𝑙 + 𝑏𝑛sin 𝑛𝜋𝑥 𝑙 4 f x x ( ) 1+ sin( ) 傅立叶级数
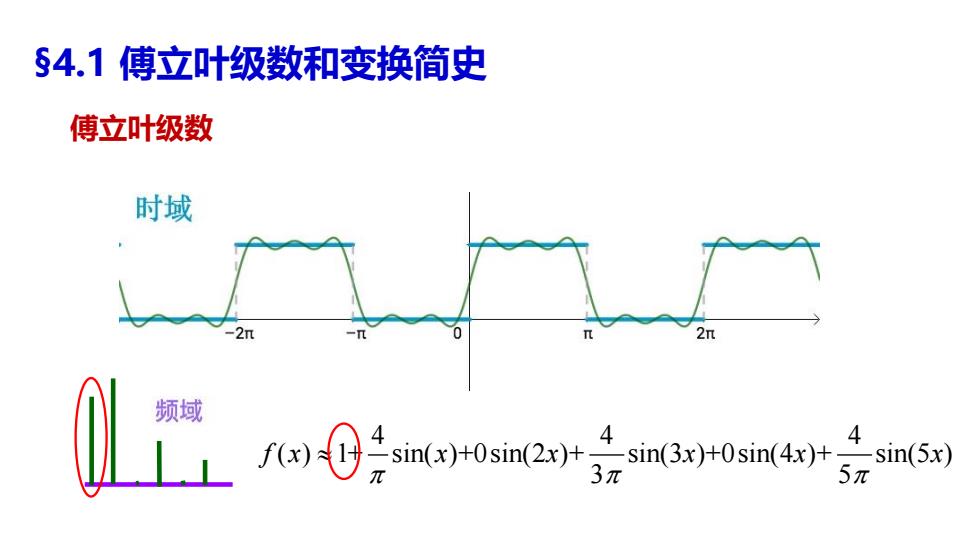
§4.1傅立叶级数和变换简史 傅立叶级数 时域 -2π 2n 频域 Lf0年试0smar年m6 in)0n5到 5元
§4.1 傅立叶级数和变换简史 傅立叶级数 4 4 4 ( ) 1+ sin( )+0sin(2 )+ sin(3 )+0sin(4 )+ sin(5 ) 3 5 f x x x x x x