
频率域滤波 ·4.1背景 ·4.2基本概念 ·4.3取样和取样函数的傅立叶变换 ·4.4单变量的离散傅立叶变换 ·4.5两个变量的扩展 ·4.6二维离散傅立叶变换的一些性质 ·4.7频率域滤波基础 ·4.8频率域滤波器平滑图像 ·4.9频率域滤波器锐化图像 ·4.10选择性滤波
• 4.1 背景 • 4.2 基本概念 • 4.3 取样和取样函数的傅立叶变换 • 4.4 单变量的离散傅立叶变换 • 4.5 两个变量的扩展 • 4.6 二维离散傅立叶变换的一些性质 • 4.7 频率域滤波基础 • 4.8 频率域滤波器平滑图像 • 4.9 频率域滤波器锐化图像 • 4.10 选择性滤波 频率域滤波
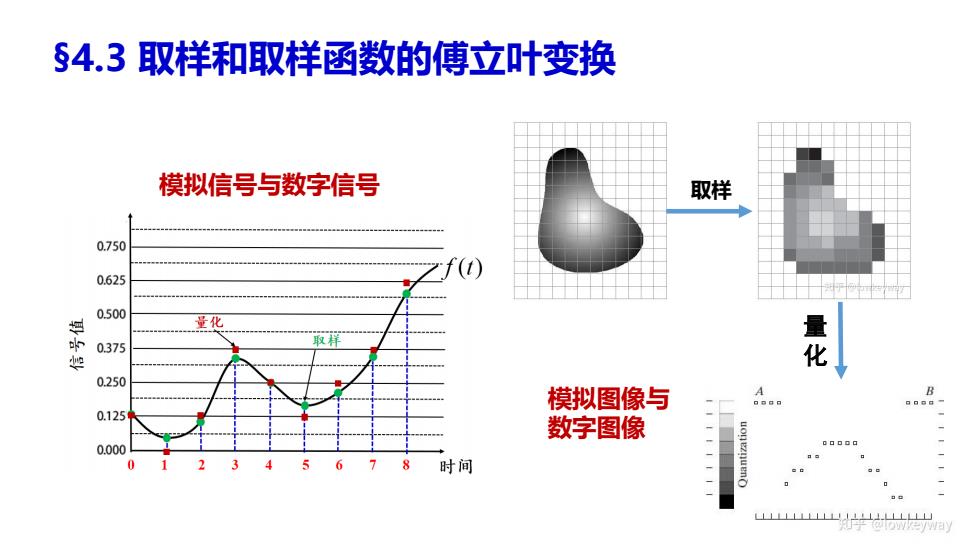
§4.3取样和取样函数的傅立叶变换 模拟信号与数字信号 取样 0.750 0.625 0.500 量化 量 0375 取样 化 0250 模拟图像与 A B 0.125 数字图像 0.000 0 5678 时间
§4.3 取样和取样函数的傅立叶变换 量 化 模拟信号与数字信号 取样 模拟图像与 数字图像
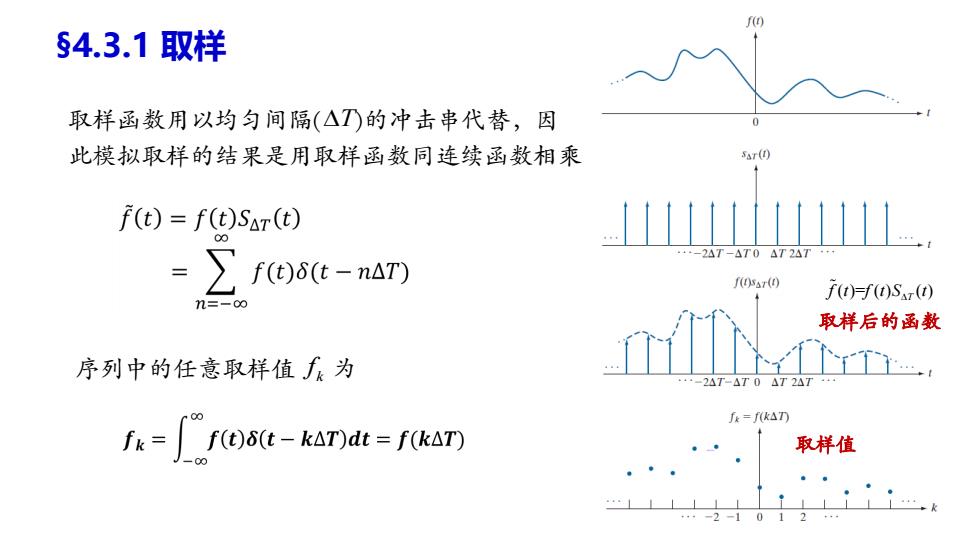
f(0 §4.3.1取样 取样函数用以均匀间隔(△T的冲击串代替,因 此模拟取样的结果是用取样函数同连续函数相乘 SAr(1) f(t)=f(t)SAr(t) =∑f()it-naT) 24T-4T04T27 f(05() f(t)f(t)Sxr(t) n=-00 取样后的函数 序列中的任意取样值,为 2△T-△T0△T2△7 fk=fk△TD fk=f(t)8(t-kAT)dt=f(kAT) 取样值 +-2-1012+…
取样函数用以均匀间隔( )的冲击串代替,因 此模拟取样的结果是用取样函数同连续函数相乘 §4.3.1 取样 T ( )= ( ) ( ) T f t f t S t 取样后的函数 序列中的任意取样值 f k 为 取样值
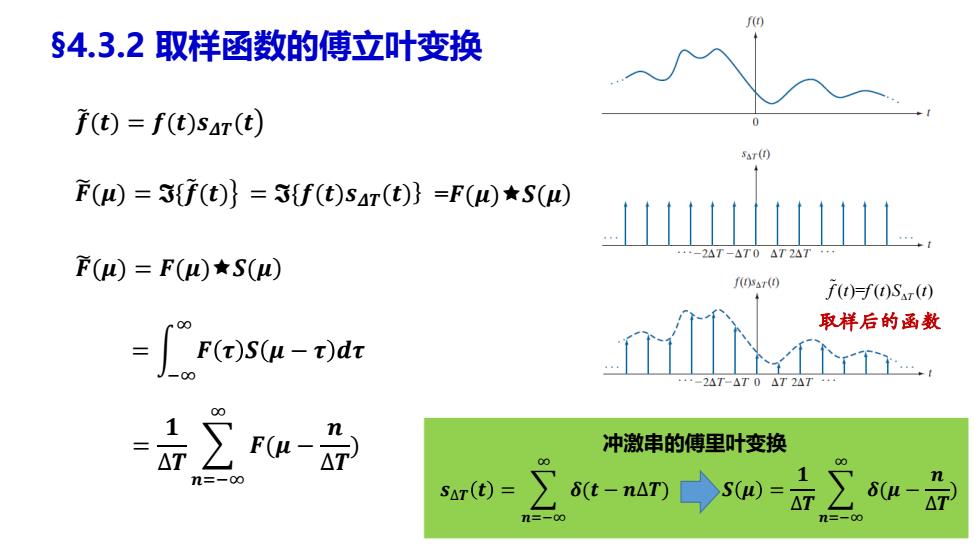
f(0 §4.3.2取样函数的傅立叶变换 f(t)f(t)sar(t) Sar(1) F(D)=3f(t)}=3f(t)sAr(t)}=F(0)★S() -2AT-AT0△T2△T·+ F())=F()★S() )sr() ft)=f0)Sr()) 取样后的函数 -["F()S(-)dr -2AT-△T0△T2A =品∑Fu- 冲激串的傅里叶变换 n=-0 SAT(t)= t-an→sw=∑s- ∑
§4.3.2 取样函数的傅立叶变换 ൯ 𝒇෨(𝒕) = 𝒇(𝒕)𝒔𝜟𝑻(𝒕 𝑭෩(𝝁) = 𝕴{ ൟ 𝒇෨(𝒕) = 𝕴{𝒇(𝒕)𝒔 ሽ 𝜟𝑻(𝒕) =𝑭(𝝁)𝑺(𝝁) 𝑭෩(𝝁) = 𝑭(𝝁)𝑺(𝝁) = න −∞ ∞ 𝑭 𝝉 𝑺 𝝁 − 𝝉 𝒅𝝉 = 𝟏 ∆𝑻 𝒏=−∞ ∞ 𝑭(𝝁 − 𝒏 ∆𝑻 ) ( )= ( ) ( ) T f t f t S t 取样后的函数 𝒔∆𝑻 𝒕 = 𝒏=−∞ ∞ 𝜹(𝒕 − 𝒏∆𝑻) 𝑺 𝝁 = 𝟏 ∆𝑻 𝒏=−∞ ∞ 𝜹(𝝁 − 𝒏 ∆𝑻 ) 冲激串的傅里叶变换
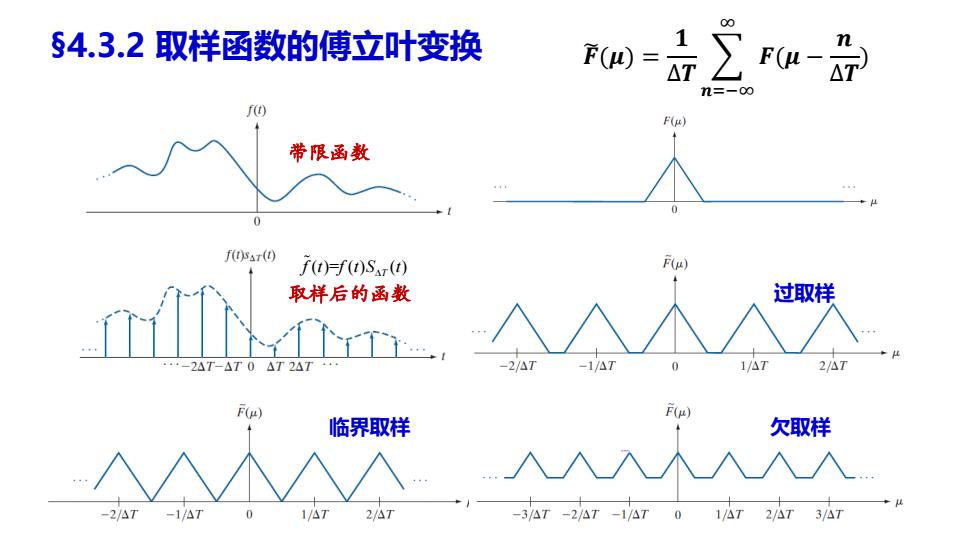
§4.3.2取样函数的傅立叶变换 Pω=∑P- f F() 带限函数 f(t)sar(t) J(t)=f(t)Sr(t) F() 取样后的函数 过取样 -2AT-△T0△T2AT+·· -2/△7 -1/△T 1/A7 F() F() 临界取样 欠取样 -2/AT -1/△7 1/△T 2/△T -3/AT-2/AT-1/AT01/△T2/△T3/A7
§4.3.2 取样函数的傅立叶变换 过取样 临界取样 欠取样 ( )= ( ) ( ) T f t f t S t 取样后的函数 带限函数 𝑭෩(𝝁) = 𝟏 ∆𝑻 𝒏=−∞ ∞ 𝑭(𝝁 − 𝒏 ∆𝑻 )
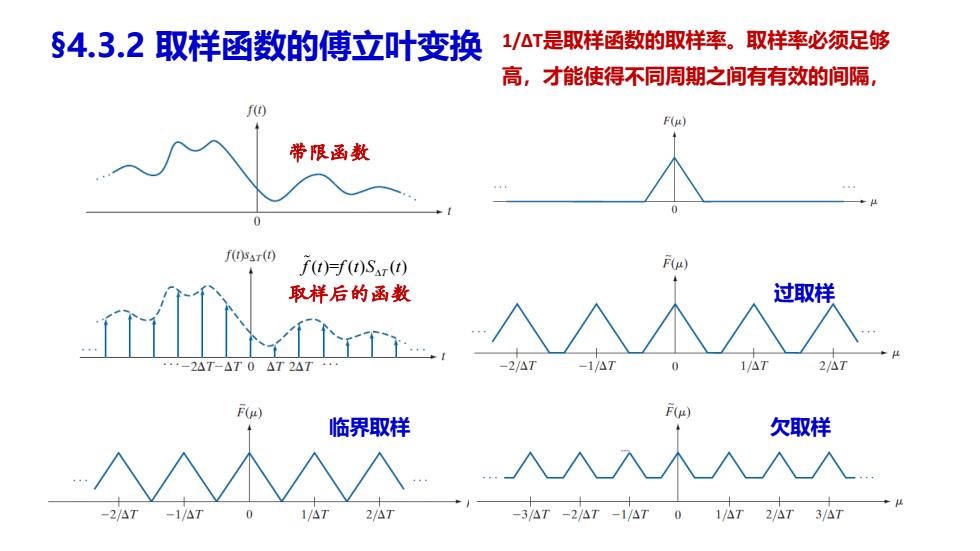
§4.3.2取样函数的傅立叶变换 1/△T是取样函数的取样率。取样率必须足够 高,才能使得不同周期之间有有效的间隔, f F(p) 带限函数 +H f05(0 f(t)f(t)Sxr() F(p) 取样后的函数 过取样 +-2AT-△T0△T2AT 44 -1/△7 F() F() 临界取样 欠取样 -2/AT -1/△7 1/AT 2/△T -3△T-2/△T-1/△T01/△T2/AT3/AT
1/∆T是取样函数的取样率。取样率必须足够 高,才能使得不同周期之间有有效的间隔, §4.3.2 取样函数的傅立叶变换 过取样 临界取样 欠取样 ( )= ( ) ( ) T f t f t S t 取样后的函数 带限函数

§4.3.3取样定理 如何给出适当条件,使得一个连续函数完全可由其取样集合来恢复? F() F() 一ma M max 一lmax 0 M max -1 0 1 2AT 2AT 取样定理 1 奈奎斯特准则 >24max 取样率非常关键
如何给出适当条件,使得一个连续函数完全可由其取样集合来恢复? 取样率非常关键 1 ∆𝑇 > 2𝜇𝑚𝑎𝑥 取样定理 奈奎斯特准则 §4.3.3 取样定理
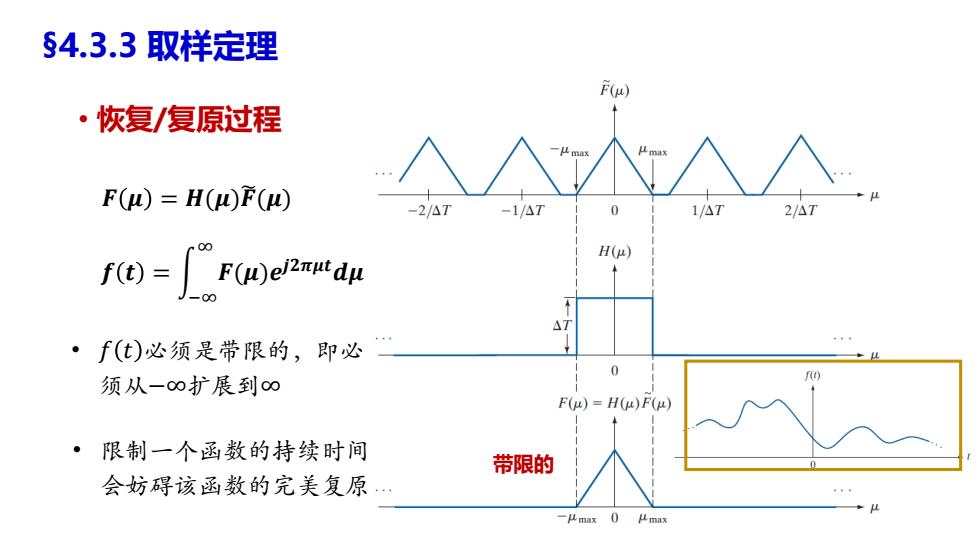
§4.3.3取样定理 F(p) ·恢复/复原过程 F()=H()F() -2/△7 -1/△7 0 1/A7 2/△T =F(p)edu H() AT ”” ·f(t)必须是带限的,即必 0 f(o 须从一∞扩展到∞ F(p)=H()F(u) 限制一个函数的持续时间 带限的 会妨碍该函数的完美复原…
• 恢复/复原过程 §4.3.3 取样定理 带限的 • 𝑓 𝑡 必须是带限的,即必 须从−∞扩展到∞ 𝒇 𝒕 = න −∞ ∞ 𝑭(𝝁)𝒆 𝒋𝟐𝝅𝝁𝒕𝒅𝝁 𝑭 𝝁 = 𝑯(𝝁)𝑭෩(𝝁) • 限制一个函数的持续时间 会妨碍该函数的完美复原
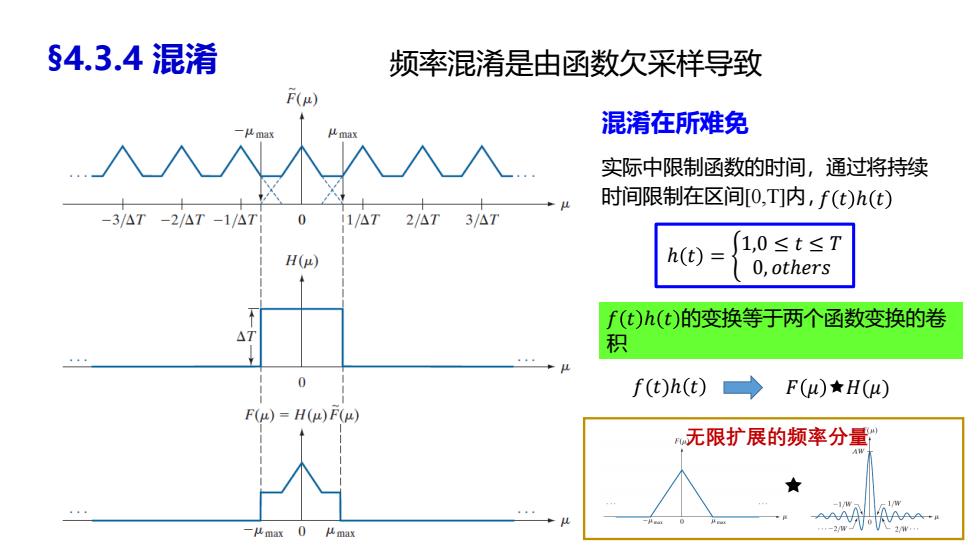
§4.3.4混淆 频率混淆是由函数欠采样导致 F(μ) 混淆在所难免 max 实际中限制函数的时间,通过将持续 时间限制在区间[0,T]内,f(t)h(t) -3/△T-2/△T-1/△T 011/△T 2/△T3/△7 1,0≤t≤T H(μ) h(t)= 0,others f(t)h(t)的变换等于两个函数变换的卷 47 积 4 0 f()h(t)→ F(u)★H() F(A)=H()F(μ) 无限扩展的频率分量 AW -11 1/ 444 4 -2W
第4章 第10页 混淆在所难免 𝑓 𝑡 ℎ 𝑡 ℎ 𝑡 = ቊ 1,0 ≤ 𝑡 ≤ 𝑇 0, 𝑜𝑡ℎ𝑒𝑟𝑠 𝑓 𝑡 ℎ 𝑡 的变换等于两个函数变换的卷 积 §4.3.4 混淆 频率混淆是由函数欠采样导致 𝑓(𝑡)ℎ 𝑡 𝐹 𝜇 𝐻(𝜇) 实际中限制函数的时间,通过将持续 时间限制在区间[0,T]内, 无限扩展的频率分量

§4.3.4混淆
§4.3.4 混淆