
频率域滤波 ·4.1背景 ·4.2基本概念 ·4.3取样和取样函数的傅立叶变换 ·4.4单变量的离散傅立叶变换 ·4.5两个变量的扩展 ·4.6二维离散傅立叶变换的一些性质 ·4.7频率域滤波基础 ·4.8频率域滤波器平滑图像 ·4.9频率域滤波器锐化图像 ·4.10选择性滤波
• 4.1 背景 • 4.2 基本概念 • 4.3 取样和取样函数的傅立叶变换 • 4.4 单变量的离散傅立叶变换 • 4.5 两个变量的扩展 • 4.6 二维离散傅立叶变换的一些性质 • 4.7 频率域滤波基础 • 4.8 频率域滤波器平滑图像 • 4.9 频率域滤波器锐化图像 • 4.10 选择性滤波 频率域滤波
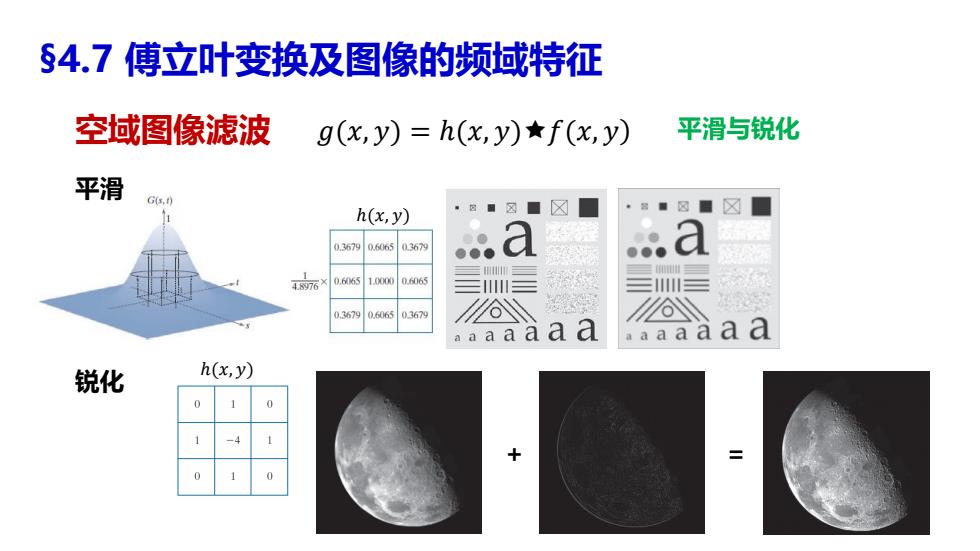
§4.7傅立叶变换及图像的频域特征 空域图像滤波 g(x,y)=h(x,y)f(x,y) 平滑与锐化 平滑 GG,1) h(x,y) ☒■ ☒ ☒ 0.3679 06065 0367 ●0 4976× 0.6065 1000 0606 三 三三 0.367 D.606 03679 aaaaa aa aa aaaa 锐化 h(x,y)
§4.7 傅立叶变换及图像的频域特征 空域图像滤波 锐化 𝑔(𝑥, 𝑦ሻ = ℎ(𝑥, 𝑦ሻ𝑓(𝑥, 𝑦ሻ 平滑 + = ℎ(𝑥, 𝑦ሻ ℎ(𝑥, 𝑦ሻ 平滑与锐化
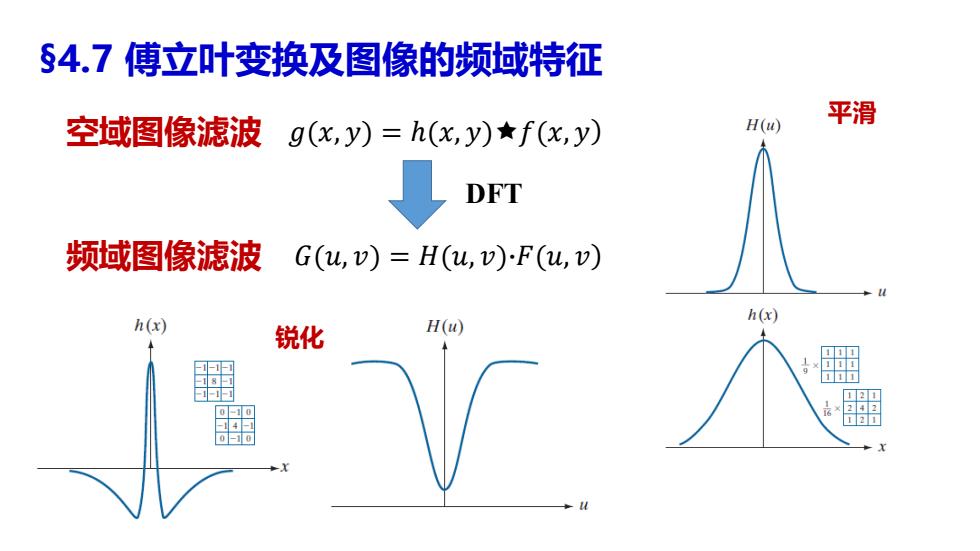
§4.7傅立叶变换及图像的频域特征 空域图像滤波g(x,y)=h(x,y)★f(x,y) H(u) 平滑 DFT 频域图像滤波 G(u,v)=H(u,v)-F(u,v) h(x) h(x) 锐化 H() -1 11m --到 o-10 × 4 0-0
空域图像滤波 𝑔(𝑥, 𝑦ሻ = ℎ(𝑥, 𝑦ሻ𝑓(𝑥, 𝑦ሻ DFT 频域图像滤波 𝐺(𝑢, 𝑣ሻ = 𝐻(𝑢, 𝑣ሻ∙𝐹(𝑢, 𝑣ሻ 平滑 锐化 §4.7 傅立叶变换及图像的频域特征
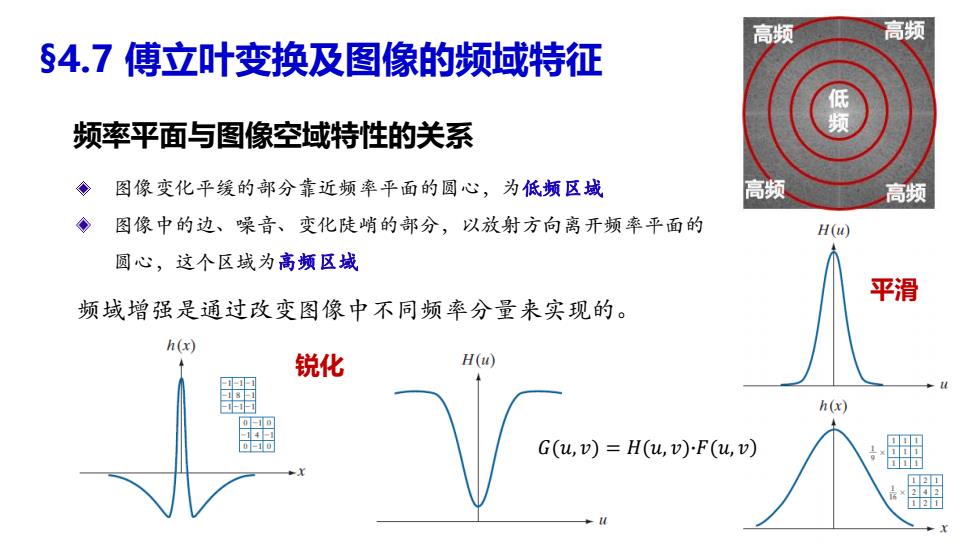
高频 高频 §4.7傅立叶变换及图像的频域特征 频率平面与图像空域特性的关系 ◆图像变化平缓的部分靠近频率平面的圆心,为低频区域 高频 ◆ 图像中的边、噪音、变化陡峭的部分,以放射方向离开频率平面的 H(u) 圆心,这个区域为高频区域 平滑 频域增强是通过改变图像中不同频率分量来实现的。 h(x) 锐化 H(u h(x) p=H4助e2o 121
频率平面与图像空域特性的关系 锐化 平滑 图像变化平缓的部分靠近频率平面的圆心,为低频区域 图像中的边、噪音、变化陡峭的部分,以放射方向离开频率平面的 圆心,这个区域为高频区域 频域增强是通过改变图像中不同频率分量来实现的。 §4.7 傅立叶变换及图像的频域特征 𝐺(𝑢, 𝑣ሻ = 𝐻(𝑢, 𝑣ሻ∙𝐹(𝑢, 𝑣ሻ

§4.7傅立叶变换及图像的频域特征 口频域滤波增强原理 傅里叶变 滤波函数 逆傅里叶 换 H(u,) 变换 F(u,) G(u,v)=F(u,v)H(u,v) 预处理 后处理 f1(x,y)=f(x,y)*(-1)x+y 关键是H(u,v)设计 f(x,y) 增强后的图像 g(x,y)
§4.7 傅立叶变换及图像的频域特征 频域滤波增强原理 预处理 𝒇(𝒙, 𝒚ሻ 傅里叶变 换 滤波函数 𝑯(𝒖, 𝒗ሻ 逆傅里叶 变换 后处理 增强后的图像 𝒈(𝒙, 𝒚ሻ 𝒇𝟏 𝒙, 𝒚 = 𝒇 𝒙, 𝒚 ∗ (−𝟏ሻ 𝒙+𝒚 𝑭(𝒖, 𝒗ሻ 𝑮 𝒖, 𝒗 = 𝑭(𝒖, 𝒗ሻ𝑯(𝒖, 𝒗ሻ 关键是𝑯(𝒖, 𝒗ሻ设计
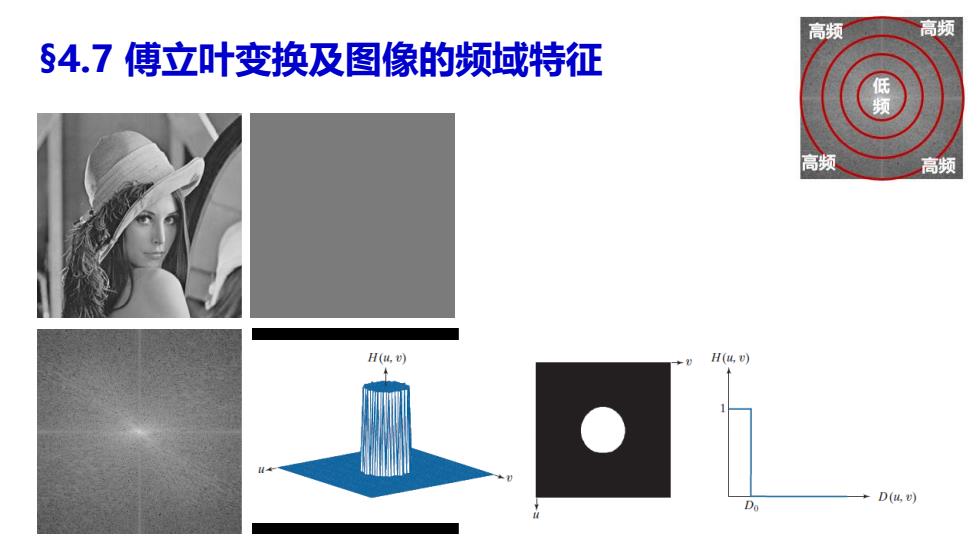
高频 高频 §4.7傅立叶变换及图像的频域特征 频 高频 高频 H(4,) H(4,) Da D(,U)
R=10 R=20 §4.7 傅立叶变换及图像的频域特征

高频 高频 §4.7傅立叶变换及图像的频域特征 低 高频 R=10 R=20
R=10 R=20 §4.7 傅立叶变换及图像的频域特征

高频 高频 §4.7傅立叶变换及图像的频域特征 ⊕ 低 频 高频 R=50 R=80
§4.7 傅立叶变换及图像的频域特征 R=50 R=80

高频 高频 §4.7傅立叶变换及图像的频域特征 高频
§4.7 傅立叶变换及图像的频域特征

§4.7傅立叶变换及图像的频域特征 口图像能量集中在低频段 图像区域能量 Fc.of a= r=00=0 ×100 R2π 图像所有能量 ∑∑IFc,o r=00=0 a99.7%a=96% a=95% a92%
2 2 0 0 2 2 0 0 ( , ) 100 ( , ) R r R r F r F r = 图像区域能量 图像所有能量 =92% =95% =99.7% =96% §4.7 傅立叶变换及图像的频域特征 图像能量集中在低频段