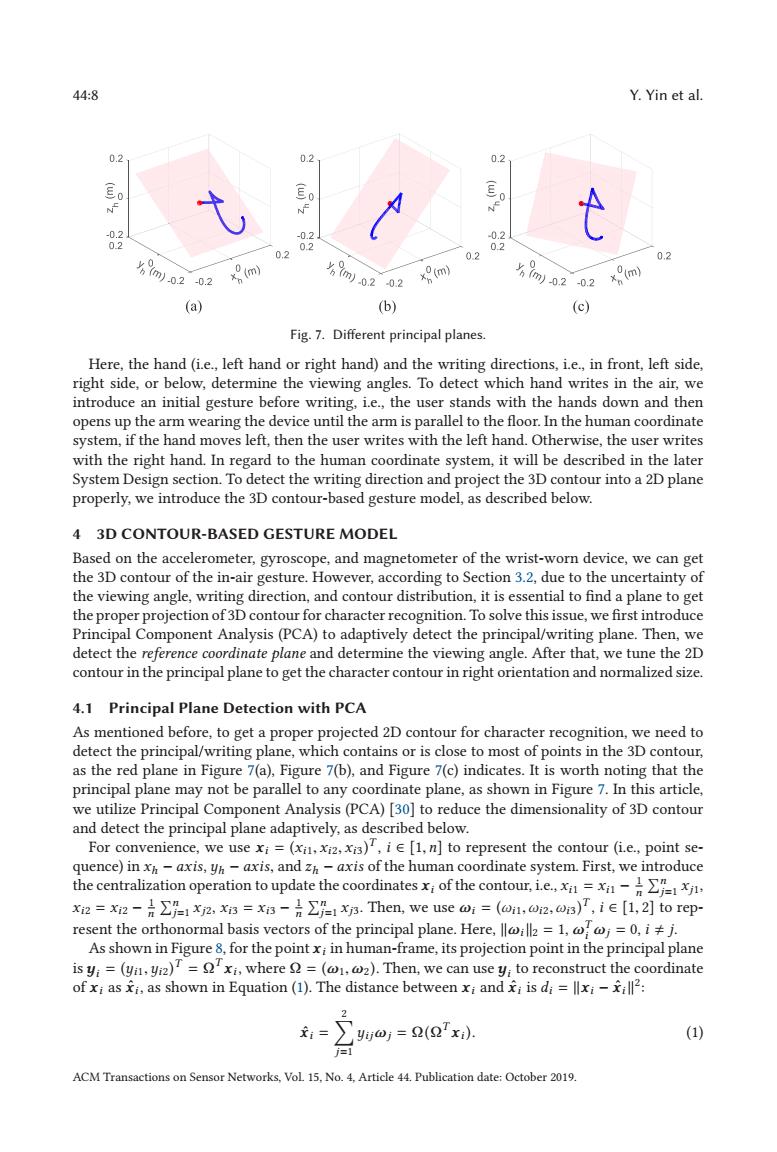
44:8 Y.Yin et al. 0.2 02 0.2 N 10 -0.2 -0.2 -0.2 02 02 02 0.2 0.2 0.2 m)02 -0.2 (m) m)0202 (m) %9m02 -0.2 x(m) (a) (b) (c) Fig.7.Different principal planes. Here,the hand (i.e.,left hand or right hand)and the writing directions,i.e.,in front,left side, right side,or below,determine the viewing angles.To detect which hand writes in the air,we introduce an initial gesture before writing,i.e.,the user stands with the hands down and then opens up the arm wearing the device until the arm is parallel to the floor.In the human coordinate system,if the hand moves left,then the user writes with the left hand.Otherwise,the user writes with the right hand.In regard to the human coordinate system,it will be described in the later System Design section.To detect the writing direction and project the 3D contour into a 2D plane properly,we introduce the 3D contour-based gesture model,as described below. 4 3D CONTOUR-BASED GESTURE MODEL Based on the accelerometer,gyroscope,and magnetometer of the wrist-worn device,we can get the 3D contour of the in-air gesture.However,according to Section 3.2,due to the uncertainty of the viewing angle,writing direction,and contour distribution,it is essential to find a plane to get the proper projection of 3D contour for character recognition.To solve this issue,we first introduce Principal Component Analysis(PCA)to adaptively detect the principal/writing plane.Then,we detect the reference coordinate plane and determine the viewing angle.After that,we tune the 2D contour in the principal plane to get the character contour in right orientation and normalized size. 4.1 Principal Plane Detection with PCA As mentioned before,to get a proper projected 2D contour for character recognition,we need to detect the principal/writing plane,which contains or is close to most of points in the 3D contour, as the red plane in Figure 7(a),Figure 7(b),and Figure 7(c)indicates.It is worth noting that the principal plane may not be parallel to any coordinate plane,as shown in Figure 7.In this article, we utilize Principal Component Analysis(PCA)[30]to reduce the dimensionality of 3D contour and detect the principal plane adaptively,as described below. For convenience,we use xi=(xi,x2,xi),ie[1,n]to represent the contour (i.e.,point se- quence)in xh-axis,yh-axis,and zh-axis of the human coordinate system.First,we introduce the centralization operation to update the coordinatesxi of the contour,i.e. xi2 =xi2-xx=x1x.Then,we use @i =(@n,0n2.0ns),ie [1,2]to rep- resent the orthonormal basis vectors of the principal plane.Here,ll=1.=0.ij. As shown in Figure 8,for the point xi in human-frame,its projection point in the principal plane isyi=(yn,yi2)=xi,where =(@@2).Then,we can use y;to reconstruct the coordinate of xi as i,as shown in Equation (1).The distance between xi and i is di=lxiil2: 2 xi= ∑wj=2(2'x. (1) j=1 ACM Transactions on Sensor Networks,Vol 15.No.4,Article 44.Publication date:October 2019.44:8 Y. Yin et al. Fig. 7. Different principal planes. Here, the hand (i.e., left hand or right hand) and the writing directions, i.e., in front, left side, right side, or below, determine the viewing angles. To detect which hand writes in the air, we introduce an initial gesture before writing, i.e., the user stands with the hands down and then opens up the arm wearing the device until the arm is parallel to the floor. In the human coordinate system, if the hand moves left, then the user writes with the left hand. Otherwise, the user writes with the right hand. In regard to the human coordinate system, it will be described in the later System Design section. To detect the writing direction and project the 3D contour into a 2D plane properly, we introduce the 3D contour-based gesture model, as described below. 4 3D CONTOUR-BASED GESTURE MODEL Based on the accelerometer, gyroscope, and magnetometer of the wrist-worn device, we can get the 3D contour of the in-air gesture. However, according to Section 3.2, due to the uncertainty of the viewing angle, writing direction, and contour distribution, it is essential to find a plane to get the proper projection of 3D contour for character recognition. To solve this issue, we first introduce Principal Component Analysis (PCA) to adaptively detect the principal/writing plane. Then, we detect the reference coordinate plane and determine the viewing angle. After that, we tune the 2D contour in the principal plane to get the character contour in right orientation and normalized size. 4.1 Principal Plane Detection with PCA As mentioned before, to get a proper projected 2D contour for character recognition, we need to detect the principal/writing plane, which contains or is close to most of points in the 3D contour, as the red plane in Figure 7(a), Figure 7(b), and Figure 7(c) indicates. It is worth noting that the principal plane may not be parallel to any coordinate plane, as shown in Figure 7. In this article, we utilize Principal Component Analysis (PCA) [30] to reduce the dimensionality of 3D contour and detect the principal plane adaptively, as described below. For convenience, we use xi = (xi1, xi2, xi3) T , i ∈ [1,n] to represent the contour (i.e., point se￾quence) in xh − axis, yh − axis, and zh − axis of the human coordinate system. First, we introduce the centralization operation to update the coordinates xi of the contour, i.e., xi1 = xi1 − 1 n n j=1 xj1, xi2 = xi2 − 1 n n j=1 xj2, xi3 = xi3 − 1 n n j=1 xj3. Then, we use ωi = (ωi1,ωi2,ωi3) T , i ∈ [1, 2] to rep￾resent the orthonormal basis vectors of the principal plane. Here, ωi2 = 1, ωT i ωj = 0, i j. As shown in Figure 8, for the point xi in human-frame, its projection point in the principal plane is yi = (yi1,yi2) T = ΩT xi , where Ω = (ω1,ω2). Then, we can use yi to reconstruct the coordinate of xi as xˆi , as shown in Equation (1). The distance between xi and xˆi is di = xi − xˆi2: xˆi = 2 j=1 yijωj = Ω(ΩT xi ). (1) ACM Transactions on Sensor Networks, Vol. 15, No. 4, Article 44. Publication date: October 2019.