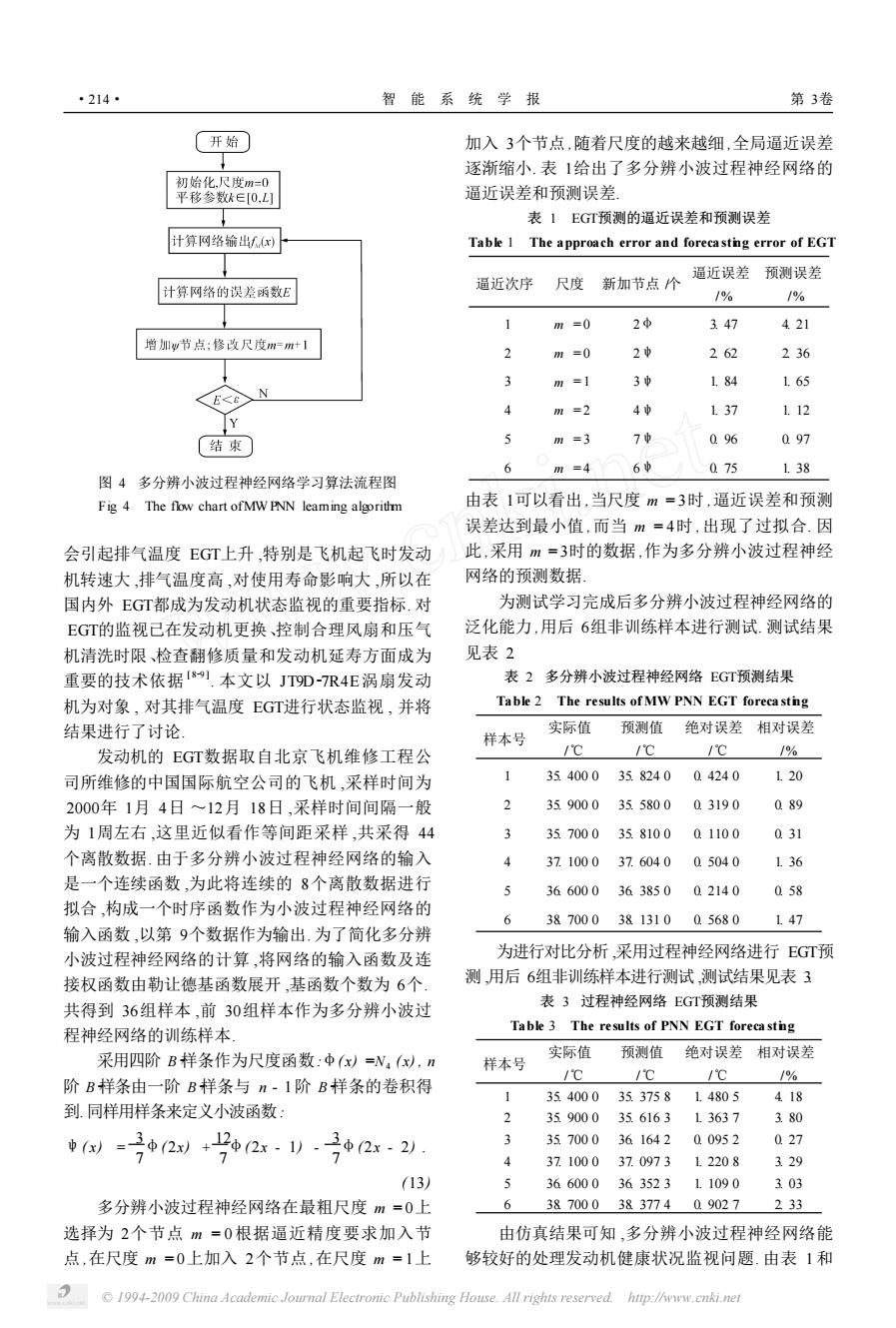
·214· 智能系统学报 第3卷 开始 加入3个节点，随着尺度的越来越细，全局逼近误差 逐渐缩小.表1给出了多分辨小波过程神经网络的 初始化，尺度m=0 平移参数k∈[0，L 逼近误差和预测误差 表1EGT预测的逼近误差和预测误差 计算网络输出f:)上 Table 1 The approach error and forecastng error of EGT 逼近误差预测误差 计算网络的误差函数E 逼近次序尺度 新加节点个 1% 1% 1 m=0 2中 347 421 增加w节点：修改尺度m=m+1 2 m=0 2中 262 236 3 m=1 3中 184 1.65 N F<E m=2 4中 137 1.12 结束 J m=3 7中 096 097 6 m=4 6中 075 1.38 图4多分辨小波过程神经网络学习算法流程图 Fig 4 The flow chart ofMW PNN leaming algorithm 由表1可以看出，当尺度m=3时，逼近误差和预测 误差达到最小值，而当m=4时，出现了过拟合，因 会引起排气温度EGT上升，特别是飞机起飞时发动 此，采用m=3时的数据，作为多分辨小波过程神经 机转速大，排气温度高，对使用寿命影响大，所以在 网络的预测数据 国内外EGT都成为发动机状态监视的重要指标.对 为测试学习完成后多分辨小波过程神经网络的 EGT的监视已在发动机更换、控制合理风扇和压气 泛化能力，用后6组非训练样本进行测试.测试结果 机清洗时限、检查翻修质量和发动机延寿方面成为 见表2 重要的技术依据[8).本文以JT9D-7R4E涡扇发动 表2多分辨小波过程神经网络EGT预测结果 机为对象，对其排气温度EGT进行状态监视，并将 Table 2 The results of MW PNN EGT forecastng 结果进行了讨论 实际值 样本号 预测值绝对误差相对误差 发动机的EGT数据取自北京飞机维修工程公 /℃ /℃ /℃ /6 司所维修的中国国际航空公司的飞机，采样时间为 354000 35.8240 04240 1.20 2000年1月4日~12月18日，采样时间间隔一般 359000 35.5800 03190 089 为1周左右，这里近似看作等间距采样，共采得44 3 357000 35.8100 01100 031 个离散数据.由于多分辨小波过程神经网络的输入 4 37.1000 37.6040 05040 1.36 是一个连续函数，为此将连续的8个离散数据进行 36600036385002140 058 拟合，构成一个时序函数作为小波过程神经网络的 6 38700038131005680 1.47 输入函数，以第9个数据作为输出.为了简化多分辨 小波过程神经网络的计算，将网络的输入函数及连 为进行对比分析，采用过程神经网络进行EGT预 接权函数由勒让德基函数展开，基函数个数为6个 测，用后6组非训练样本进行测试，测试结果见表3 共得到36组样本，前30组样本作为多分辨小波过 表3过程神经网络EGT预测结果 程神经网络的训练样本. Table 3 The results of PNN EGT forecastng 采用四阶B样条作为尺度函数：中(x)=N,(x),n 实际值 预测值 绝对误差相对误差 样本号 /℃ /℃ /℃ /% 阶B样条由一阶B样条与n-1阶B样条的卷积得 1 35400035.375814805 418 到.同样用样条来定义小波函数： 35900035616313637 3.80 1似=02划+42).2-2 3 35700036164200952 027 7 7 4 37100037.097312208 329 (13) 5 3660003635231.1090 303 多分辨小波过程神经网络在最粗尺度m=0上 638700038377409027233 选择为2个节点m=0根据逼近精度要求加入节 由仿真结果可知，多分辨小波过程神经网络能 点，在尺度m=0上加入2个节点，在尺度m=1上 够较好的处理发动机健康状况监视问题.由表1和 1994-2009 China Academic Journal Electronic Publishing House.All rights reserved http://www.cnki.net图 4 多分辨小波过程神经网络学习算法流程图 Fig. 4 The flow chart ofMW PNN learning algorithm 会引起排气温度 EGT上升 ,特别是飞机起飞时发动 机转速大 ,排气温度高 ,对使用寿命影响大 ,所以在 国内外 EGT都成为发动机状态监视的重要指标. 对 EGT的监视已在发动机更换、控制合理风扇和压气 机清洗时限、检查翻修质量和发动机延寿方面成为 重要的技术依据 [ 829 ] . 本文以 JT9D27R4E涡扇发动 机为对象 , 对其排气温度 EGT进行状态监视 , 并将 结果进行了讨论. 发动机的 EGT数据取自北京飞机维修工程公 司所维修的中国国际航空公司的飞机 ,采样时间为 2000年 1月 4日 ～12月 18日 ,采样时间间隔一般 为 1周左右 ,这里近似看作等间距采样 ,共采得 44 个离散数据. 由于多分辨小波过程神经网络的输入 是一个连续函数 ,为此将连续的 8个离散数据进行 拟合 ,构成一个时序函数作为小波过程神经网络的 输入函数 ,以第 9个数据作为输出. 为了简化多分辨 小波过程神经网络的计算 ,将网络的输入函数及连 接权函数由勒让德基函数展开 ,基函数个数为 6个. 共得到 36组样本 ,前 30组样本作为多分辨小波过 程神经网络的训练样本. 采用四阶 B 2样条作为尺度函数:φ( x) =N4 ( x) , n 阶 B 2样条由一阶 B 2样条与 n - 1阶 B 2样条的卷积得 到.同样用样条来定义小波函数: ψ( x) = 3 7 φ(2x) + 12 7 φ(2x - 1) - 3 7 φ(2x - 2) . (13) 多分辨小波过程神经网络在最粗尺度 m = 0上 选择为 2个节点 m = 0根据逼近精度要求加入节 点 ,在尺度 m = 0上加入 2个节点 ,在尺度 m = 1上 加入 3个节点 ,随着尺度的越来越细 ,全局逼近误差 逐渐缩小. 表 1给出了多分辨小波过程神经网络的 逼近误差和预测误差. 表 1 EGT预测的逼近误差和预测误差 Table 1 The approach error and foreca sting error of EGT 逼近次序 尺度 新加节点 /个 逼近误差 /% 预测误差 /% 1 m = 0 2φ 3. 47 4. 21 2 m = 0 2ψ 2. 62 2. 36 3 m = 1 3ψ 1. 84 1. 65 4 m = 2 4ψ 1. 37 1. 12 5 m = 3 7ψ 0. 96 0. 97 6 m = 4 6ψ 0. 75 1. 38 由表 1可以看出 ,当尺度 m = 3时 ,逼近误差和预测 误差达到最小值 ,而当 m = 4时 ,出现了过拟合. 因 此 ,采用 m = 3时的数据 ,作为多分辨小波过程神经 网络的预测数据. 为测试学习完成后多分辨小波过程神经网络的 泛化能力 ,用后 6组非训练样本进行测试. 测试结果 见表 2. 表 2 多分辨小波过程神经网络 EGT预测结果 Table 2 The results of MW PNN EGT foreca sting 样本号 实际值 /℃ 预测值 /℃ 绝对误差 /℃ 相对误差 /% 1 35. 400 0 35. 824 0 0. 424 0 1. 20 2 35. 900 0 35. 580 0 0. 319 0 0. 89 3 35. 700 0 35. 810 0 0. 110 0 0. 31 4 37. 100 0 37. 604 0 0. 504 0 1. 36 5 36. 600 0 36. 385 0 0. 214 0 0. 58 6 38. 700 0 38. 131 0 0. 568 0 1. 47 为进行对比分析 ,采用过程神经网络进行 EGT预 测 ,用后 6组非训练样本进行测试 ,测试结果见表 3. 表 3 过程神经网络 EGT预测结果 Table 3 The results of PNN EGT foreca sting 样本号 实际值 /℃ 预测值 /℃ 绝对误差 /℃ 相对误差 /% 1 35. 400 0 35. 375 8 1. 480 5 4. 18 2 35. 900 0 35. 616 3 1. 363 7 3. 80 3 35. 700 0 36. 164 2 0. 095 2 0. 27 4 37. 100 0 37. 097 3 1. 220 8 3. 29 5 36. 600 0 36. 352 3 1. 109 0 3. 03 6 38. 700 0 38. 377 4 0. 902 7 2. 33 由仿真结果可知 ,多分辨小波过程神经网络能 够较好的处理发动机健康状况监视问题. 由表 1 和 ·214· 智 能 系 统 学 报 第 3卷 © 1994-2009 China Academic Journal Electronic Publishing House. All rights reserved. http://www.cnki.net