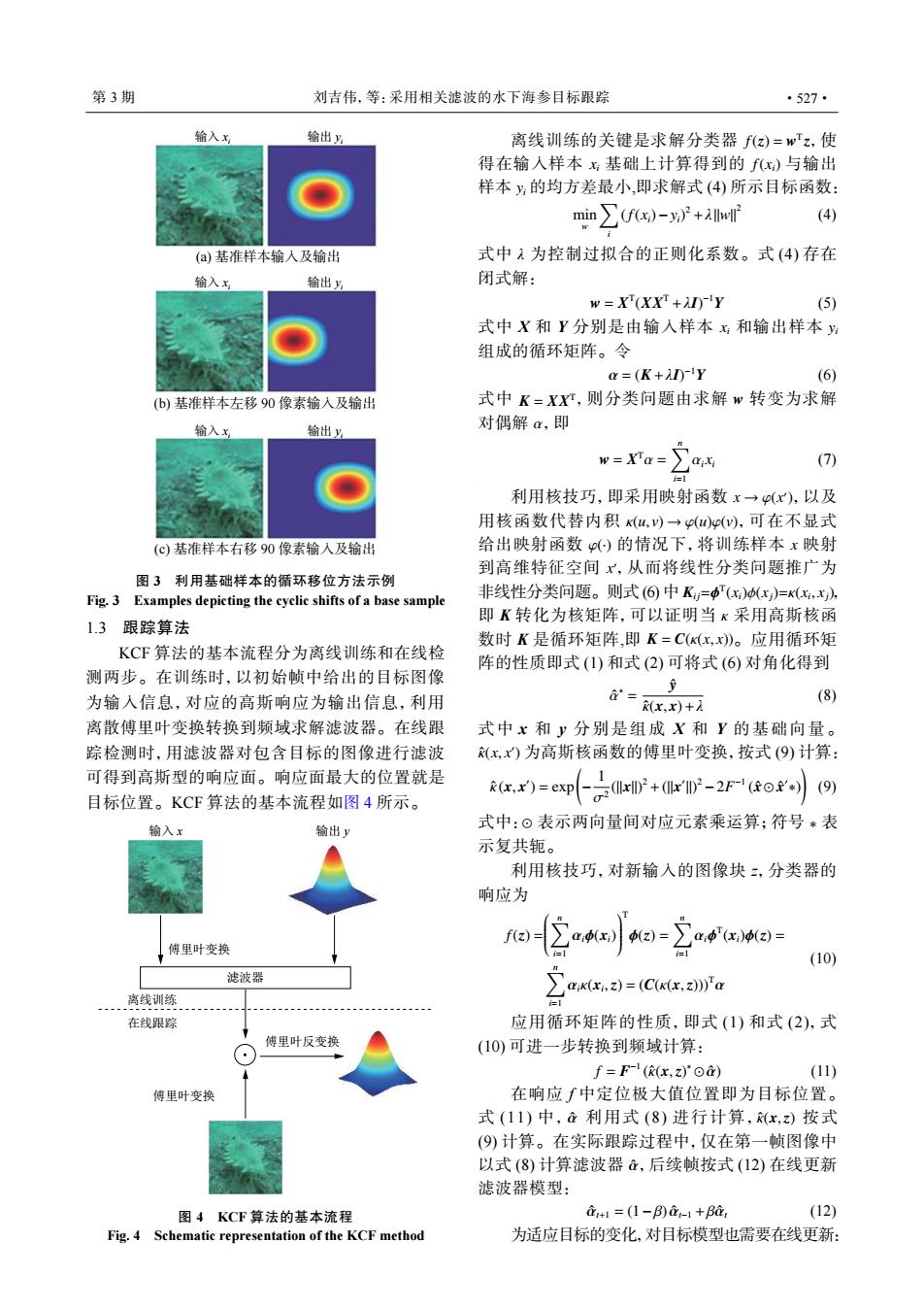
第3期 刘吉伟，等：采用相关滤波的水下海参目标跟踪 ·527· 输入x 输出y 离线训练的关键是求解分类器fz)=wz,使 得在输入样本：基础上计算得到的f(x)与输出 样本y的均方差最小，即求解式(4)所示目标函数： min∑fx)-y2+awf (4) (a)基准样本输入及输出 式中1为控制过拟合的正则化系数。式(4)存在 输入x 输出 闭式解： w=X(XXT+Y (5) 式中X和Y分别是由输人样本：和输出样本 组成的循环矩阵。令 a=(K+-Y (6) (b)基准样本左移90像素输入及输出 式中K=Xx,则分类问题由求解w转变为求解 输入x 输出y 对偶解α，即 w=Xa= (7) i=l 利用核技巧，即采用映射函数x→(x),以及 用核函数代替内积u,)→0)p(m),可在不显式 (©)基准样本右移90像素输入及输出 给出映射函数()的情况下，将训练样本x映射 到高维特征空间x,从而将线性分类问题推广为 图3利用基础样本的循环移位方法示例 Fig.3 Examples depicting the cyclic shifts of a base sample 非线性分类问题。则式（⑥中K=中T(x)(x)=K(x,x》 即K转化为核矩阵，可以证明当k采用高斯核函 1.3跟踪算法 数时K是循环矩阵，即K=C((x,x)。应用循环矩 KCF算法的基本流程分为离线训练和在线检 阵的性质即式(1)和式(2)可将式(6)对角化得到 测两步。在训练时，以初始帧中给出的目标图像 为输入信息，对应的高斯响应为输出信息，利用 a=x,x)+ (8) 离散傅里叶变换转换到频域求解滤波器。在线跟 式中x和y分别是组成X和Y的基础向量。 踪检测时，用滤波器对包含目标的图像进行滤波 (x,x)为高斯核函数的傅里叶变换，按式（⑨）计算： 可得到高斯型的响应面。响应面最大的位置就是 1 目标位置。KCF算法的基本流程如图4所示。 Rx,)=expD产+rD2-2F'住o到(9) 输入x 输出)y 式中：⊙表示两向量间对应元素乘运算：符号*表 示复共轭。 利用核技巧，对新输入的图像块，分类器的 响应为 傅里叶变换 ro-o-wo- (10) 滤波器 ..离线训练 aw(C.'a 在线跟踪 应用循环矩阵的性质，即式(1)和式(2)，式 傅里叶反变换 (10)可进一步转换到频域计算： f=F-((x,z)'⊙d) (11) 傅里叶变换 在响应∫中定位极大值位置即为目标位置。 式(11)中，d利用式(8)进行计算，(x,z)按式 (9)计算。在实际跟踪过程中，仅在第一帧图像中 以式(8)计算滤波器à，后续帧按式(12)在线更新 滤波器模型： 图4KCF算法的基本流程 d+1=(1-B)d-1+Ba (12) Fig.4 Schematic representation of the KCF method 为适应目标的变化，对目标模型也需要在线更新：(a) 基准样本输入及输出 (b) 基准样本左移 90 像素输入及输出 (c) 基准样本右移 90 像素输入及输出 输入 xi 输出 yi 输入 xi 输出 yi 输入 xi 输出 yi 图 3 利用基础样本的循环移位方法示例 Fig. 3 Examples depicting the cyclic shifts of a base sample 1.3 跟踪算法 KCF 算法的基本流程分为离线训练和在线检 测两步。在训练时，以初始帧中给出的目标图像 为输入信息，对应的高斯响应为输出信息，利用 离散傅里叶变换转换到频域求解滤波器。在线跟 踪检测时，用滤波器对包含目标的图像进行滤波 可得到高斯型的响应面。响应面最大的位置就是 目标位置。KCF 算法的基本流程如图 4 所示。 输出 y 傅里叶变换 傅里叶变换 傅里叶反变换 离线训练 在线跟踪 滤波器 输入 x 图 4 KCF 算法的基本流程 Fig. 4 Schematic representation of the KCF method f(z) = w T z xi f(xi) yi 离线训练的关键是求解分类器 ，使 得在输入样本 基础上计算得到的 与输出 样本 的均方差最小,即求解式 (4) 所示目标函数： min w ∑ i (f(xi)−yi) 2 +λ ∥w∥ 2 (4) 式中 λ 为控制过拟合的正则化系数。式 (4) 存在 闭式解： w = X T (XXT +λI) −1Y (5) 式中 X 和 Y 分别是由输入样本 xi 和输出样本 yi 组成的循环矩阵。令 α = (K +λI) −1Y (6) K = XXT w α 式中 ，则分类问题由求解 转变为求解 对偶解 ，即 w = X Tα = ∑n i=1 αixi (7) x → φ(x ′ ) κ(u, v) → φ(u)φ(v) φ(·) x x ′ Ki j=ϕ T (xi)ϕ(xj)=κ(xi , xj) κ K = C(κ(x, x)) 利用核技巧，即采用映射函数 ，以及 用核函数代替内积 ，可在不显式 给出映射函数 的情况下，将训练样本 映射 到高维特征空间 ，从而将线性分类问题推广为 非线性分类问题。则式 (6) 中 ， 即 K 转化为核矩阵，可以证明当 采用高斯核函 数时 K 是循环矩阵,即 。应用循环矩 阵的性质即式 (1) 和式 (2) 可将式 (6) 对角化得到 αˆ ∗ = yˆ κˆ(x, x)+λ (8) κˆ(x, x ′ ) 式中 x 和 y 分别是组成 X 和 Y 的基础向量。 为高斯核函数的傅里叶变换，按式 (9) 计算： κˆ (x, x ′ ) = exp( − 1 σ2 (∥x∥) 2 +(∥x ′ ∥) 2 −2F −1 (xˆ ⊙ xˆ ′ ∗) ) (9) 式中： ⊙ 表示两向量间对应元素乘运算；符号 ∗ 表 示复共轭。 利用核技巧，对新输入的图像块 z，分类器的 响应为 f(z) =   ∑n i=1 αiϕ(xi)   T ϕ(z) = ∑n i=1 αiϕ T (xi)ϕ(z) = ∑n i=1 αiκ(xi ,z) = (C(κ(x,z)))Tα (10) 应用循环矩阵的性质，即式 (1) 和式 (2)，式 (10) 可进一步转换到频域计算： f = F −1 (κˆ(x,z) ∗ ⊙αˆ) (11) αˆ κˆ(x,z) αˆ 在响应 f 中定位极大值位置即为目标位置。 式 (11) 中 ， 利用式 (8) 进行计算， 按式 (9) 计算。在实际跟踪过程中，仅在第一帧图像中 以式 (8) 计算滤波器 ，后续帧按式 (12) 在线更新 滤波器模型： αˆt+1 = (1−β)αˆt−1 +βαˆt (12) 为适应目标的变化，对目标模型也需要在线更新： 第 3 期 刘吉伟，等：采用相关滤波的水下海参目标跟踪 ·527·