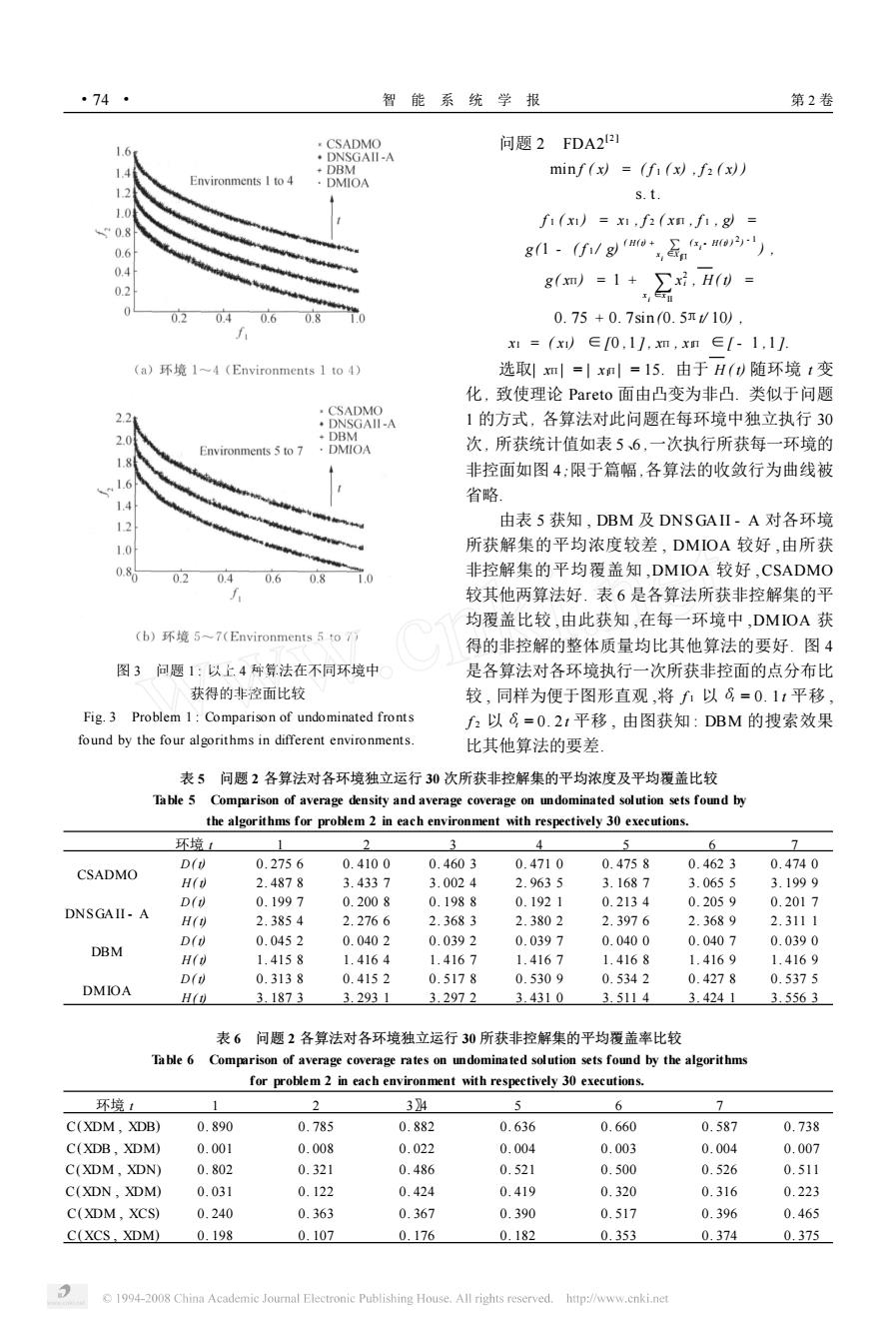
74 智能系统学报 第2卷 ￥CSADMO 1.6 问题2FDA2I ·DNSGAII-A 1.4 DBM minf(x)=(f1(x).f2(x)) Environments I to 4 ·DMIOA 1.2 s.t. 1.0 fi(x)x1,f2(xn,fi,g)= 0.8 0.6 g1-f/g0+￡n. 0.4 0.2 g(xm)=1+x好，H()= ,安 0.2 0.40.6 少汽0 0.8 0.75+0.7sin0.5r/10), x1=(x∈0,1]，xm,xm∈[-1,1]. (a)环境14(Environments1to4) 选取！m=|xm=15.由于H()随环境t变 化，致使理论Pareto面由凸变为非凸.类似于问题 ·CSADMO 2.2 ·DNSGAII-A 1的方式，各算法对此问题在每环境中独立执行30 2.0 +DBM Environments 5 to 7 ·DMIOA 次，所获统计值如表56，一次执行所获每一环境的 1.8 非控面如图4：限于篇幅，各算法的收敛行为曲线被 1.6 1.4 省略 12 由表5获知，DBM及DNSGAII-A对各环境 1.0 所获解集的平均浓度较差，DMIOA较好，由所获 085 020.40.60.8 1.0 非控解集的平均覆盖知，DMIOA较好，CSADMO 较其他两算法好.表6是各算法所获非控解集的平 均覆盖比较，由此获知，在每一环境中，DMIOA获 (b)环境5~7(Environments5tof 得的非控解的整体质量均比其他算法的要好.图4 图3问题1：以上.4种算法在不同环境中 是各算法对各环境执行一次所获非控面的点分布比 获得的非控面比较 较，同样为便于图形直观，将f1以8=0.11平移 Fig.3 Problem 1:Comparison of undominated fronts f2以8=0.21平移，由图获知：DBM的搜索效果 found by the four algorithms in different environments. 比其他算法的要差 表5问题2各算法对各环境独立运行30次所获非控解集的平均浓度及平均覆盖比较 Table 5 Comparison of average density and average coverage on undominated solution sets found by the algorithms for problem 2 in each environment with respectively 30 executions. 环境 1 2 3 4 5 6 7 D(v 0.2756 0.4100 0.4603 0.4710 0.4758 0.4623 0.4740 CSADMO H(v 2.4878 3.4337 3.0024 2.9635 3.1687 3.0655 3.1999 D(v 0.1997 0.2008 0.1988 0.1921 0.2134 0.2059 0.2017 DNSGAII-A H() 2.3854 2.2766 2.3683 2.3802 2.3976 2.3689 2.3111 D(0 0.0452 0.0402 0.0392 0.0397 0.0400 0.0407 0.0390 DBM H(0 1.4158 1.4164 1.4167 1.4167 1.4168 1.4169 1.4169 D(d 0.3138 0.4152 0.5178 0.5309 0.5342 0.4278 0.5375 DMIOA H(n) 3.1873 3.2931 3.2972 3.4310 3.5114 3.4241 3.5563 表6问题2各算法对各环境独立运行30所获非控解集的平均覆盖率比较 Table 6 Comparison of average coverage rates on undominated solution sets found by the algorithms for problem 2 in each environment with respectively 30 executions. 环境t 1 2 34 6 1 C(XDM,X①B) 0.890 0.785 0.882 0.636 0.660 0.587 0.738 C(XDB,XDM) 0.001 0.008 0.022 0.004 0.003 0.004 0.007 C(XDM,XDN) 0.802 0.321 0.486 0.521 0.500 0.526 0.511 C(XDN.XDM) 0.031 0.122 0.424 0.419 0.320 0.316 0.223 C(XDM.XCS) 0.240 0.363 0.367 0.390 0.517 0.396 0.465 C(XCS,XDM) 0.198 0.107 0.176 0.182 0.353 0.374 0.375 1994-2008 China Academic Journal Electronic Publishing House.All rights reserved. http://www.cnki.net图 3 问题 1 : 以上 4 种算法在不同环境中 获得的非控面比较 Fig. 3 Problem 1 : Comparison of undominated fronts found by the four algorithms in different environments. 问题 2 FDA2 [2 ] min f ( x) = ( f 1 ( x) , f 2 ( x) ) s. t. f 1 ( x1 ) = x1 , f 2 ( xIΠ , f 1 , g) = g (1 - ( f 1 / g) ( H( t) + x ∑i ∈XΠI ( x i - H( t) ) 2 ) - 1 ) , g ( xΠ) = 1 + x i∑∈x II x 2 i , H ( t) = 0. 75 + 0. 7sin (0. 5πt/ 10) , xI = ( xI) ∈[0 ,1 ] , xΠ , xIΠ ∈[ - 1 ,1 ]. 选取| xΠ| = | xIΠ| = 15. 由于 H ( t) 随环境 t 变 化 , 致使理论 Pareto 面由凸变为非凸. 类似于问题 1 的方式 , 各算法对此问题在每环境中独立执行 30 次 , 所获统计值如表 5、6 ,一次执行所获每一环境的 非控面如图 4 ;限于篇幅 ,各算法的收敛行为曲线被 省略. 由表 5 获知 , DBM 及 DNSGAII - A 对各环境 所获解集的平均浓度较差 , DMIOA 较好 ,由所获 非控解集的平均覆盖知 ,DMIOA 较好 ,CSADMO 较其他两算法好. 表 6 是各算法所获非控解集的平 均覆盖比较 ,由此获知 ,在每一环境中 ,DMIOA 获 得的非控解的整体质量均比其他算法的要好. 图 4 是各算法对各环境执行一次所获非控面的点分布比 较 , 同样为便于图形直观 ,将 f 1 以δt = 0. 1 t 平移 , f 2 以δt = 0. 2t 平移 , 由图获知 : DBM 的搜索效果 比其他算法的要差. 表 5 问题 2 各算法对各环境独立运行 30 次所获非控解集的平均浓度及平均覆盖比较 Table 5 Comparison of average density and average coverage on undominated solution sets found by the algorithms for problem 2 in each environment with respectively 30 executions. 环境 t 1 2 3 4 5 6 7 CSADMO D( t) 0. 275 6 0. 410 0 0. 460 3 0. 471 0 0. 475 8 0. 462 3 0. 474 0 H( t) 2. 487 8 3. 433 7 3. 002 4 2. 963 5 3. 168 7 3. 065 5 3. 199 9 DNSGAII - A D( t) 0. 199 7 0. 200 8 0. 198 8 0. 192 1 0. 213 4 0. 205 9 0. 201 7 H( t) 2. 385 4 2. 276 6 2. 368 3 2. 380 2 2. 397 6 2. 368 9 2. 311 1 DBM D( t) 0. 045 2 0. 040 2 0. 039 2 0. 039 7 0. 040 0 0. 040 7 0. 039 0 H( t) 1. 415 8 1. 416 4 1. 416 7 1. 416 7 1. 416 8 1. 416 9 1. 416 9 DMIOA D( t) 0. 313 8 0. 415 2 0. 517 8 0. 530 9 0. 534 2 0. 427 8 0. 537 5 H( t) 3. 187 3 3. 293 1 3. 297 2 3. 431 0 3. 511 4 3. 424 1 3. 556 3 表 6 问题 2 各算法对各环境独立运行 30 所获非控解集的平均覆盖率比较 Table 6 Comparison of average coverage rates on undominated solution sets found by the algorithms for problem 2 in each environment with respectively 30 executions. 环境 t 1 2 3〗4 5 6 7 C(XDM , XDB) 0. 890 0. 785 0. 882 0. 636 0. 660 0. 587 0. 738 C(XDB , XDM) 0. 001 0. 008 0. 022 0. 004 0. 003 0. 004 0. 007 C(XDM , XDN) 0. 802 0. 321 0. 486 0. 521 0. 500 0. 526 0. 511 C(XDN , XDM) 0. 031 0. 122 0. 424 0. 419 0. 320 0. 316 0. 223 C(XDM , XCS) 0. 240 0. 363 0. 367 0. 390 0. 517 0. 396 0. 465 C(XCS , XDM) 0. 198 0. 107 0. 176 0. 182 0. 353 0. 374 0. 375 · 47 · 智 能 系 统 学 报 第 2 卷