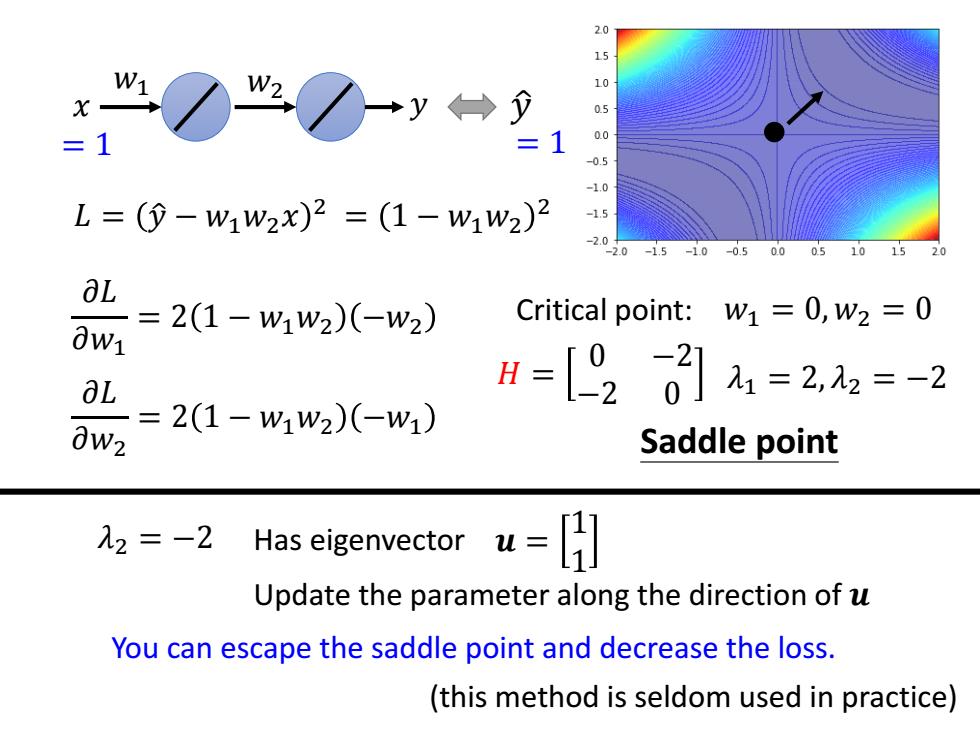
20 15 W2 +y←→ 09 1.0 L=(⊙-w1w2x)2=(1-w1w2)2 -15 2.0 2.0 -1.5 -1.0 -0.5 0.0 05 =21-w1w2)-w） Critical point: W1=0,W2=0 0W1 0L=2(1-ww2)(-w1） H=[920]=2,=-2 0W2 Saddle point =-2 Has sigenvector Update the parameter along the direction of u You can escape the saddle point and decrease the loss. (this method is seldom used in practice)𝐿 = 𝑦 ො − 𝑤1𝑤2𝑥 2 𝜕𝐿 𝜕𝑤1 = 2 1 − 𝑤1𝑤2 −𝑤2 𝜕𝐿 𝜕𝑤2 = 2 1 − 𝑤1𝑤2 −𝑤1 𝑤1 𝑤2 𝑥 𝑦 𝑦 ො = 1 = 1 = 1 − 𝑤1𝑤2 2 Critical point: 𝑤1 = 0, 𝑤2 = 0 𝐻 = 0 −2 −2 0 𝜆1 = 2, 𝜆2 = −2 Saddle point Has eigenvector 𝒖 = 1 1 𝜆2 = −2 You can escape the saddle point and decrease the loss. Update the parameter along the direction of 𝒖 (this method is seldom used in practice)