
When gradient is small .. Hung-yi Lee李宏毅
When gradient is small … Hung-yi Lee 李宏毅
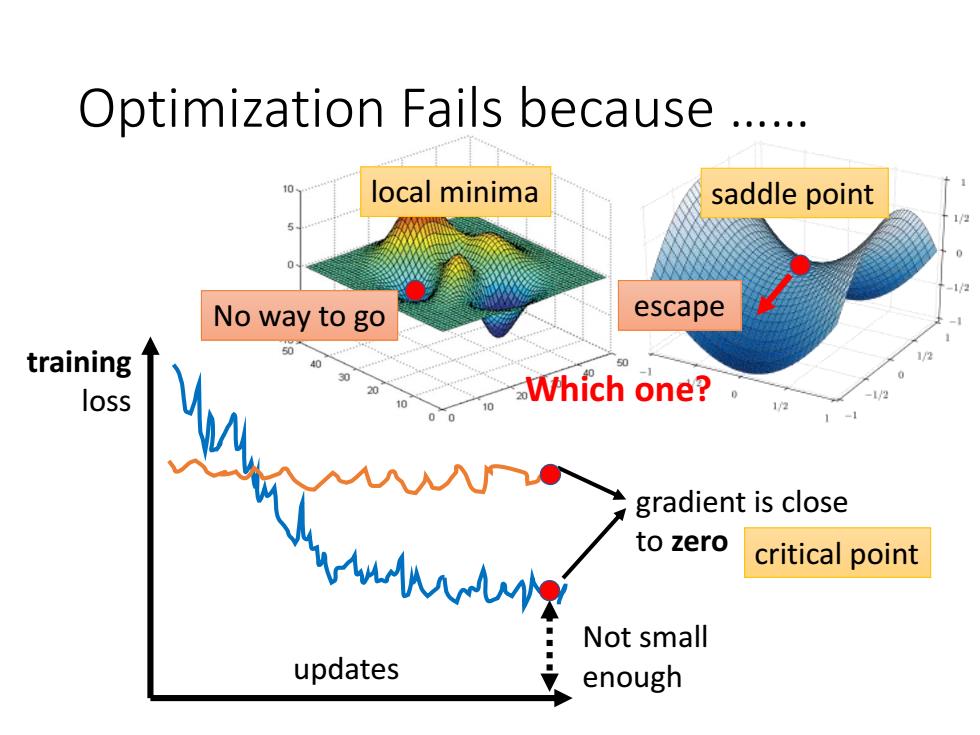
Optimization Fails because ..... local minima saddle point No way to go escape training 40 50 loss 00 0 Which one?。 1/2 gradient is close to zero critical point Not small updates enough
local minima Optimization Fails because …… updates training loss Not small enough gradient is close to zero saddle point critical point Which one? No way to go escape

Warning of Math
Warning of Math

Tayler Series Approximation L(g)aroundθ=θ'can be approximated below L(0)≈L(a)+0-8)rg+E(0-g)H(g-g) Gradient g is a vector aL(0) g=7L(0) gi=001 L(0) Hessian H is a matrix 02 Hi=0010 、L(0')
Tayler Series Approximation 𝐿 𝜽 ≈ 𝐿 𝜽 ′ + 𝜽 − 𝜽 ′ 𝑇𝒈 + 1 2 𝜽 − 𝜽 ′ 𝑇𝐻 𝜽 − 𝜽 ′ Gradient 𝒈 is a vector Hessian 𝐻 is a matrix 𝒈𝑖 = 𝜕𝐿 𝜽 ′ 𝜕𝜽𝑖 𝐻𝑖𝑗 = 𝜕 2 𝜕𝜽𝑖𝜕𝜽𝑗 𝐿 𝜽 ′ 𝒈 = 𝛻𝐿 𝜽 ′ 𝐿 𝜽 around 𝜽 = 𝜽 ′ can be approximated below 𝜽 ′ 𝜽 𝐿 𝜽
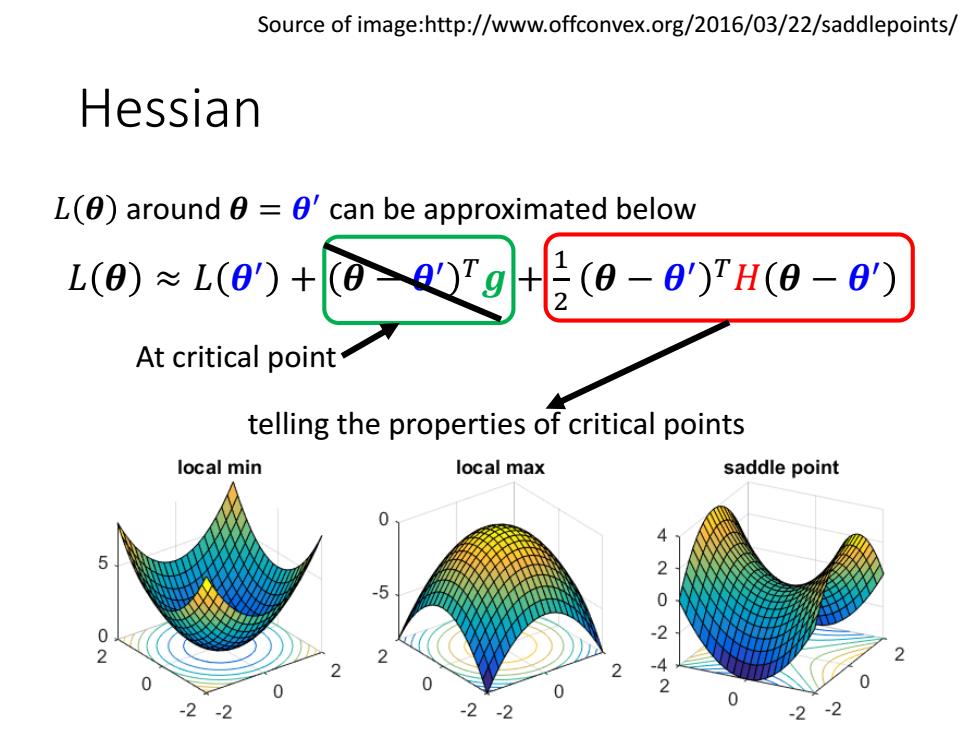
Source of image:http://www.offconvex.org/2016/03/22/saddlepoints/ Hessian L()around =0'can be approximated below L(0)*1(9)+00☑叶60-9H6-0y At critical point telling the properties of critical points local min local max saddle point 4 2 0 0 0 -2-2 -2-2 -2
Hessian Source of image:http://www.offconvex.org/2016/03/22/saddlepoints/ telling the properties of critical points 𝐿 𝜽 ≈ 𝐿 𝜽 ′ + 𝜽 − 𝜽 ′ 𝑇𝒈 + 1 2 𝜽 − 𝜽 ′ 𝑇𝐻 𝜽 − 𝜽 ′ 𝐿 𝜽 around 𝜽 = 𝜽 ′ can be approximated below At critical point

At critical point: vTHv Hessian 1 L(8)≈L(8)t(8-8)H(8-8) For all v vTHv>0→ Around 0':L(O)>L(θ')→Local minima H is positive definite All eigen values are positive. For all v vTHv0,sometimes vHv<0 Saddle point Some eigen values are positive,and some are negative
Hessian At critical point: 𝐻 is positive definite 𝒗 𝑇𝐻𝒗 > 0 Around 𝜽 Local minima ′ : 𝐿 𝜽 > 𝐿 𝜽 ′ All eigen values are positive. 𝒗 𝑇𝐻𝒗 0, sometimes 𝒗 𝑇𝐻𝒗 < 0 Saddle point 𝒗 𝑇𝐻𝒗 𝐿 𝜽 ≈ 𝐿 𝜽 ′ + 1 2 𝜽 − 𝜽 ′ 𝑇𝐻 𝜽 − 𝜽 ′ Around 𝜽 ′ : 𝐿 𝜽 < 𝐿 𝜽 ′ = = = 𝐻 is negative definite = All eigen values are negative. Some eigen values are positive, and some are negative. For all 𝒗 For all 𝒗
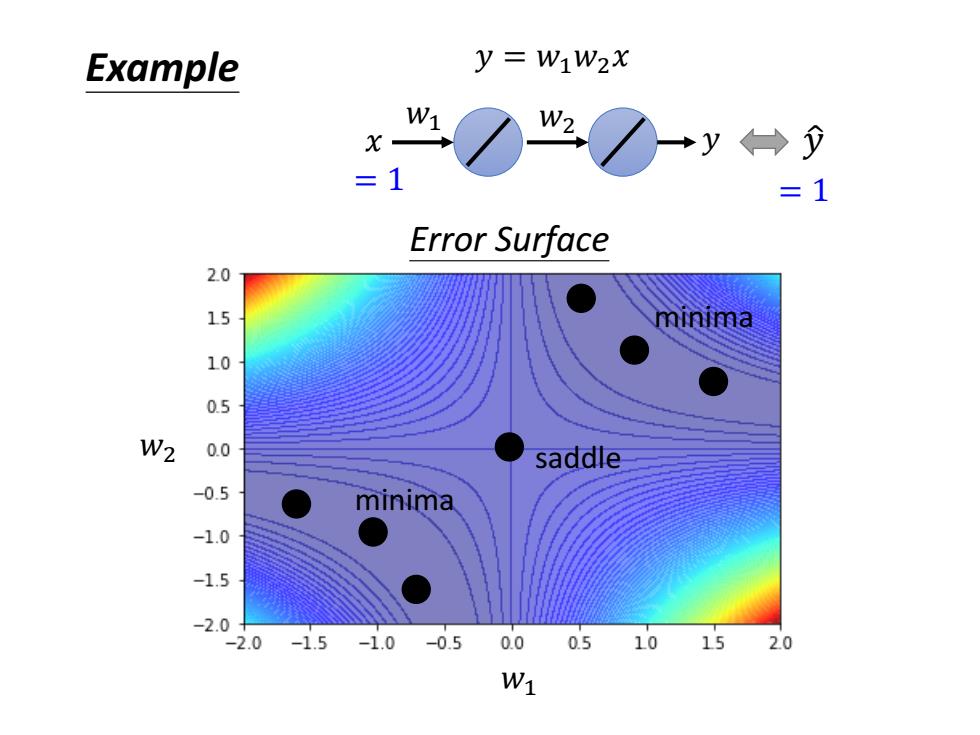
Example y=W1W2X W1 W2 →y←→ =1 =1 Error Surface 2.0 15 minima 10 W2 0.0 saddle -0.5 minima -1.0 -1.5 -2.0 2.0 -1.5 -1.0 -0.5 0.0 0.5 10 15 20 W1
𝑤1 𝑤2 𝑥 𝑦 𝑦 ො = 1 = 1 𝑦 = 𝑤1𝑤2𝑥 Example 𝑤1 𝑤2 Error Surface saddle minima minima

20 15 W1 W2 y →夕 106 =1 0.5 o L=(⊙-w1w2x)2=(1-w1w2)2 15 2.0 .0 -15 -10 -0.5 0.0 05 10 15 0W1 2(1-w1w2)(-w2) Critical point: W1=0,W2=0 =0 aL H=[9201a=22=-2 0W2 2(1-w1w2)(-w1) Saddle point =0 021 2(-w2)(-w2) 02L 0w1 -2+4W1W2 H =0 0w1∂w, =-2 02L -2+4W1W2 0w20W1 2(-w1)(-w1) =-2 =0
𝐿 = 𝑦 ො − 𝑤1𝑤2𝑥 2 𝜕𝐿 𝜕𝑤1 = 2 1 − 𝑤1𝑤2 −𝑤2 𝜕𝐿 𝜕𝑤2 = 2 1 − 𝑤1𝑤2 −𝑤1 𝜕 2𝐿 𝜕𝑤1 2 = 2 −𝑤2 −𝑤2 𝜕 2𝐿 𝜕𝑤2 2 = 2 −𝑤1 −𝑤1 𝜕 2𝐿 𝜕𝑤1𝜕𝑤2 = −2 + 4𝑤1𝑤2 𝜕 2𝐿 𝜕𝑤2𝜕𝑤1 = −2 + 4𝑤1𝑤2 𝑤1 𝑤2 𝑥 𝑦 𝑦 ො = 1 = 1 = 1 − 𝑤1𝑤2 2 Critical point: 𝑤1 = 0, 𝑤2 = 0 𝐻 = 0 −2 −2 0 𝜆1 = 2, 𝜆2 = −2 Saddle point = 0 = 0 = 0 = −2 = 0 = −2 𝒈 𝐻

Don't afraid of saddle point? vTHv At critical point:L()L(+-)TH(-0' Sometimes vTHv>0,sometimes vTHv<0 Saddle point H may tell us parameter update direction! u is an eigen vector of H →uTHu=u(2u)=lul2 λis the eigen value of u λ<0 <0 <0 1 u L(0)≈L(0)+2(0-8)TH(0-6)→L(0)<L(8) 0-0'=2u 0=0'+u Decrease L
𝐿 𝜽 ≈ 𝐿 𝜽 ′ + 1 2 𝜽 − 𝜽 ′ 𝑇𝐻 𝜽 − 𝜽 ′ Sometimes 𝒗 𝑇𝐻𝒗 > 0, sometimes 𝒗 𝑇𝐻𝒗 < 0 Saddle point 𝒖 is an eigen vector of 𝐻 𝒖 𝑇𝐻𝒖 = 𝒖 𝑇 𝜆𝒖 = 𝜆 𝒖 2 𝜆 is the eigen value of 𝒖 𝐻 may tell us parameter update direction! 𝜆 < 0 < 0 < 0 At critical point: 𝒗 𝑇𝐻𝒗 Don’t afraid of saddle point? 𝒖 𝒖 𝐿 𝜽 < 𝐿 𝜽 ′ 𝜽 = 𝜽 ′ + 𝒖 Decrease 𝐿 𝐿 𝜽 ≈ 𝐿 𝜽 ′ + 1 2 𝜽 − 𝜽 ′ 𝑇𝐻 𝜽 − 𝜽 ′ 𝜽 − 𝜽 ′ = 𝒖
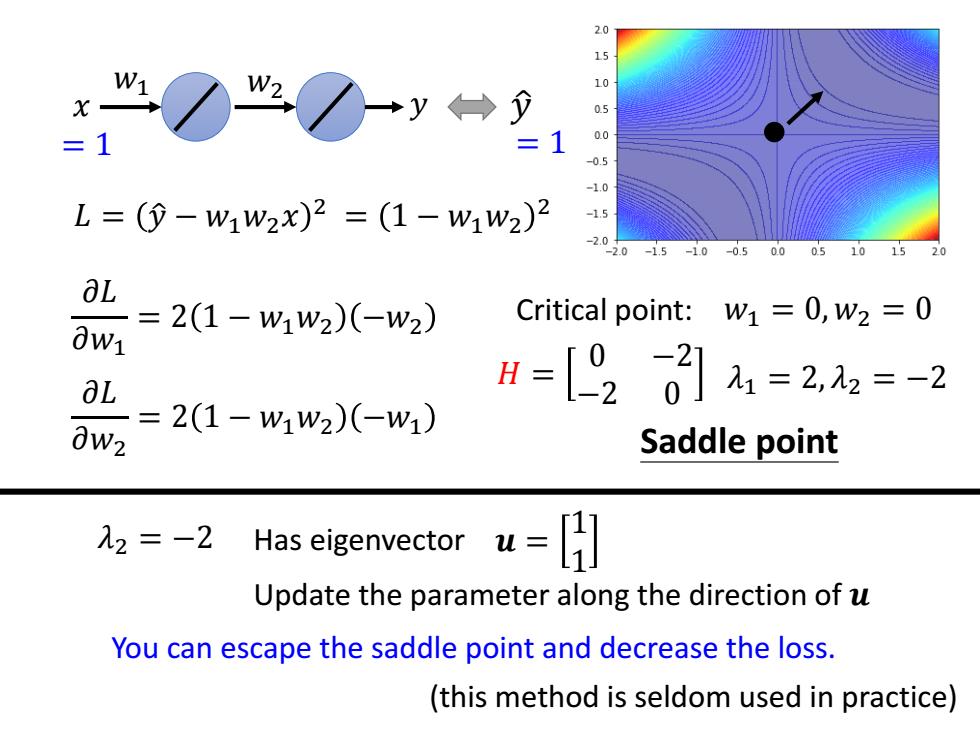
20 15 W2 +y←→ 09 1.0 L=(⊙-w1w2x)2=(1-w1w2)2 -15 2.0 2.0 -1.5 -1.0 -0.5 0.0 05 =21-w1w2)-w) Critical point: W1=0,W2=0 0W1 0L=2(1-ww2)(-w1) H=[920]=2,=-2 0W2 Saddle point =-2 Has sigenvector Update the parameter along the direction of u You can escape the saddle point and decrease the loss. (this method is seldom used in practice)
𝐿 = 𝑦 ො − 𝑤1𝑤2𝑥 2 𝜕𝐿 𝜕𝑤1 = 2 1 − 𝑤1𝑤2 −𝑤2 𝜕𝐿 𝜕𝑤2 = 2 1 − 𝑤1𝑤2 −𝑤1 𝑤1 𝑤2 𝑥 𝑦 𝑦 ො = 1 = 1 = 1 − 𝑤1𝑤2 2 Critical point: 𝑤1 = 0, 𝑤2 = 0 𝐻 = 0 −2 −2 0 𝜆1 = 2, 𝜆2 = −2 Saddle point Has eigenvector 𝒖 = 1 1 𝜆2 = −2 You can escape the saddle point and decrease the loss. Update the parameter along the direction of 𝒖 (this method is seldom used in practice)