
《神经网络与深度学习》 前馈神经网络 https://nndl.github.io/
前馈神经网络 《神经⽹络与深度学习》 https://nndl.github.io/

内容 神经网络 神经元 网络结构 ↓前馈神经网络 参数学习 计算图与自动微分 ,优化问题 《神经网络与深度学习》 2
《神经⽹络与深度学习》 2 内容 }神经⽹络 }神经元 }⽹络结构 }前馈神经⽹络 }参数学习 }计算图与自动微分 }优化问题

神经网络
神经网络

神经网络 神经网络最早是作为一种主要的连接主义模型。 20世纪80年代后期,最流行的一种连接主义模型是分布式并行处理 (Parallel Distributed Processing,PDP)网络,其有3个主要特性: 1)信息表示是分布式的(非局部的); 2)记忆和知识是存储在单元之间的连接上; 3)通过逐渐改变单元之间的连接强度来学习新的知识。 引入误差反向传播来改进其学习能力之后,神经网络也越来越多地 应用在各种机器学习任务上。 《神经网络与深度学习》
《神经⽹络与深度学习》 4 神经网络 }神经⽹络最早是作为⼀种主要的连接主义模型。 }20世纪80年代后期,最流⾏的⼀种连接主义模型是分布式并⾏处理 (Parallel Distributed Processing,PDP)⽹络,其有3个主要特性: }1)信息表示是分布式的(非局部的); }2)记忆和知识是存储在单元之间的连接上; }3)通过逐渐改变单元之间的连接强度来学习新的知识。 }引⼊误差反向传播来改进其学习能⼒之后,神经⽹络也越来越多地 应用在各种机器学习任务上

神经元
神经元
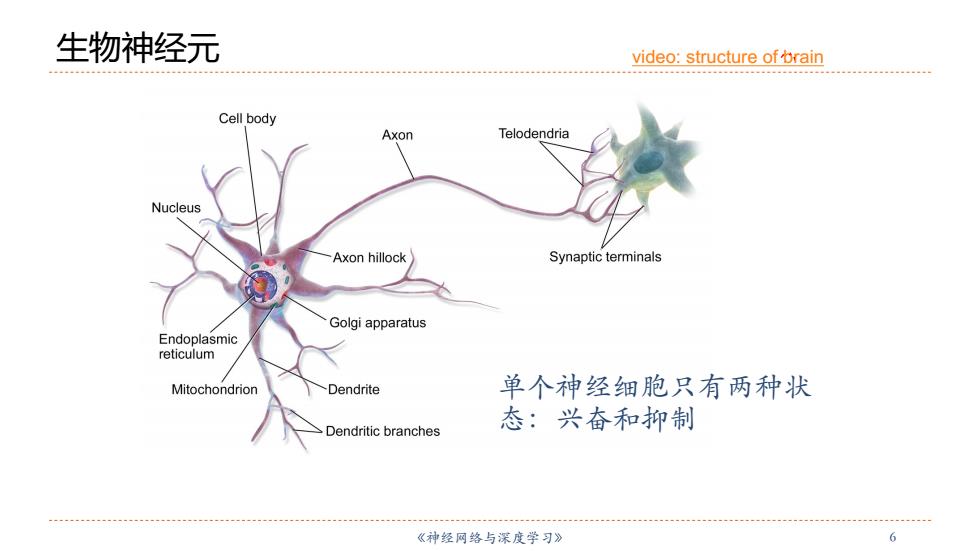
生物神经元 video:structure of brain Cell body Axon Telodendria Nucleus Axon hillock Synaptic terminals Golgi apparatus Endoplasmic reticulum Mitochondrion Dendrite 单个神经细胞只有两种状 Dendritic branches 态:兴奋和抑制 《神经网络与深度学习》 6
《神经⽹络与深度学习》 6 生物神经元 单个神经细胞只有两种状 态:兴奋和抑制 video: structure of brain
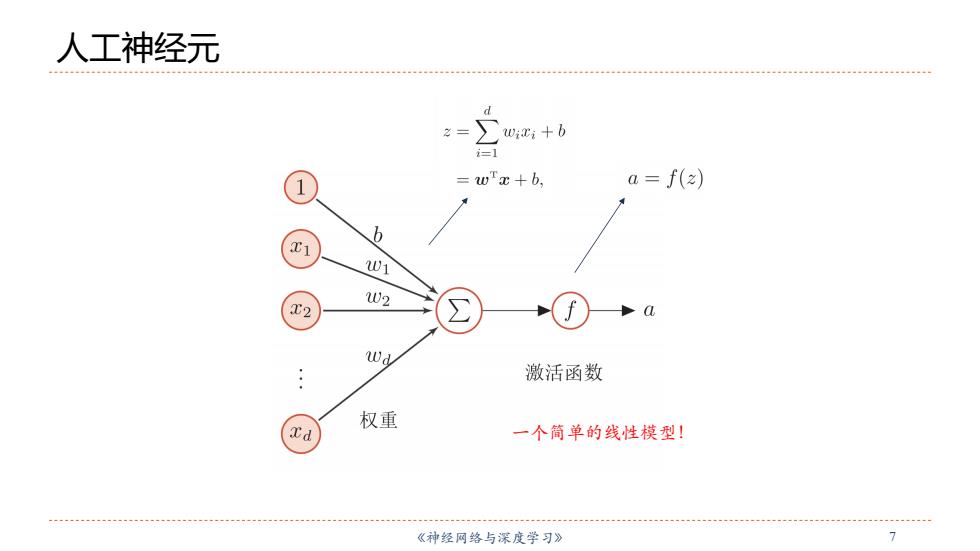
人工神经元 Wixi +b =wTx+b, a f(z) 6 W1 W2 Wd 激活函数 权重 一个筒单的线性模型! 《神经网络与深度学习》 7
《神经⽹络与深度学习》 7 人工神经元 ⼀个简单的线性模型!

激活函数的性质 连续并可导(允许少数,点上不可导)的非线性函数。 可导的激活函数可以直接利用数值优化的方法来学习网络参数。 激活函数及其导函数要尽可能的简单 有利于提高网络计算效率。 激活函数的导函数的值域要在一个合适的区间内 不能太大也不能太小,否则会影响训练的效率和稳定性。 单调递增 ??2 《神经网络与深度学习》
《神经⽹络与深度学习》 8 激活函数的性质 }连续并可导(允许少数点上不可导)的非线性函数。 }可导的激活函数可以直接利用数值优化的⽅法来学习⽹络参数。 }激活函数及其导函数要尽可能的简单 }有利于提⾼⽹络计算效率。 }激活函数的导函数的值域要在⼀个合适的区间内 }不能太⼤也不能太小,否则会影响训练的效率和稳定性。 }单调递增 }???
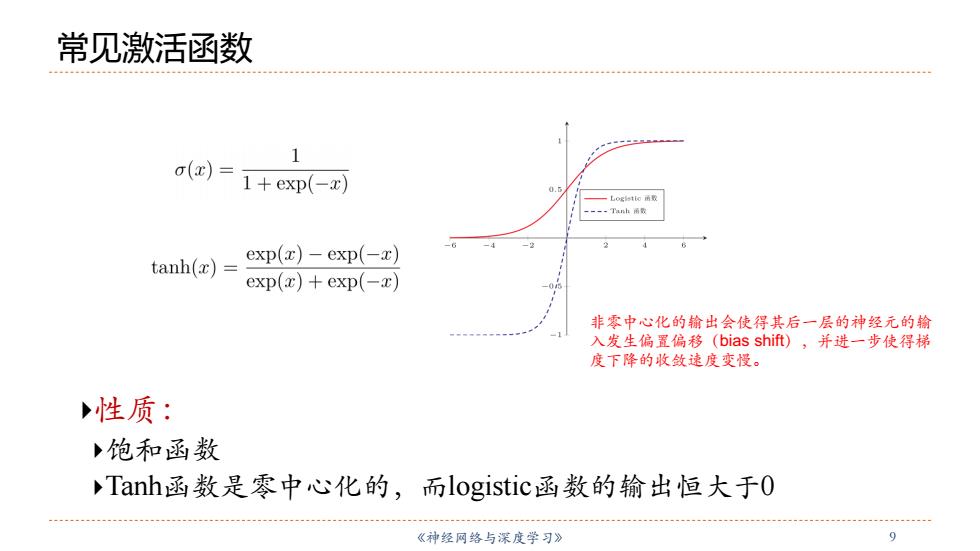
常见激活函数 ………… 1 o(x)= 1+exp(-x) 0. 一L0gsto函取 -=--Tnh雨圆 tanh(x)= exp(z)-exp(-z) exp(x)+exp(-2) 非零中心化的输出会使得其后一层的神经元的输 入发生偏置偏移(bias shift),并进一步使得梯 度下降的收敛速度变慢。 性质: 饱和函数 Tanh函数是零中心化的,而logistic函数的输出恒大于0 《神经网络与深度学习》 9
《神经⽹络与深度学习》 9 常见激活函数 非零中⼼化的输出会使得其后⼀层的神经元的输 ⼊发⽣偏置偏移(bias shift),并进⼀步使得梯 度下降的收敛速度变慢。 }性质: }饱和函数 }Tanh函数是零中⼼化的,⽽logistic函数的输出恒⼤于0
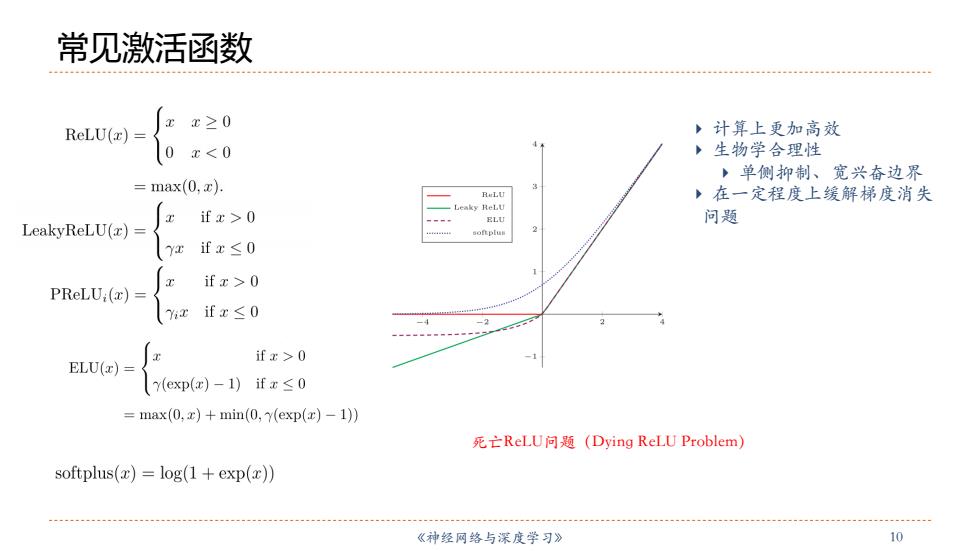
常见激活函数 x≥0 ReLU(z) ,计算上更加高效 0 x0 ELU 问题 LeakyReLU(z)= 2 (Y2 ifx≤0 if x>0 PReLU:(x) ifx≤0 -4 if x>0 ELU(z) Y(exp(e)-1)ifx≤0 =max(0,x)+min(0,y(exp(r)-1)) 死亡ReL.U问题(Dying ReLU Problem) softplus()=log(1+exp(x)) 《神经网络与深度学习》 10
《神经⽹络与深度学习》 10 常见激活函数 } 计算上更加⾼效 } ⽣物学合理性 } 单侧抑制、宽兴奋边界 } 在⼀定程度上缓解梯度消失 问题 死亡ReLU问题(Dying ReLU Problem)