
Tips for Deep Learning
Tips for Deep Learning
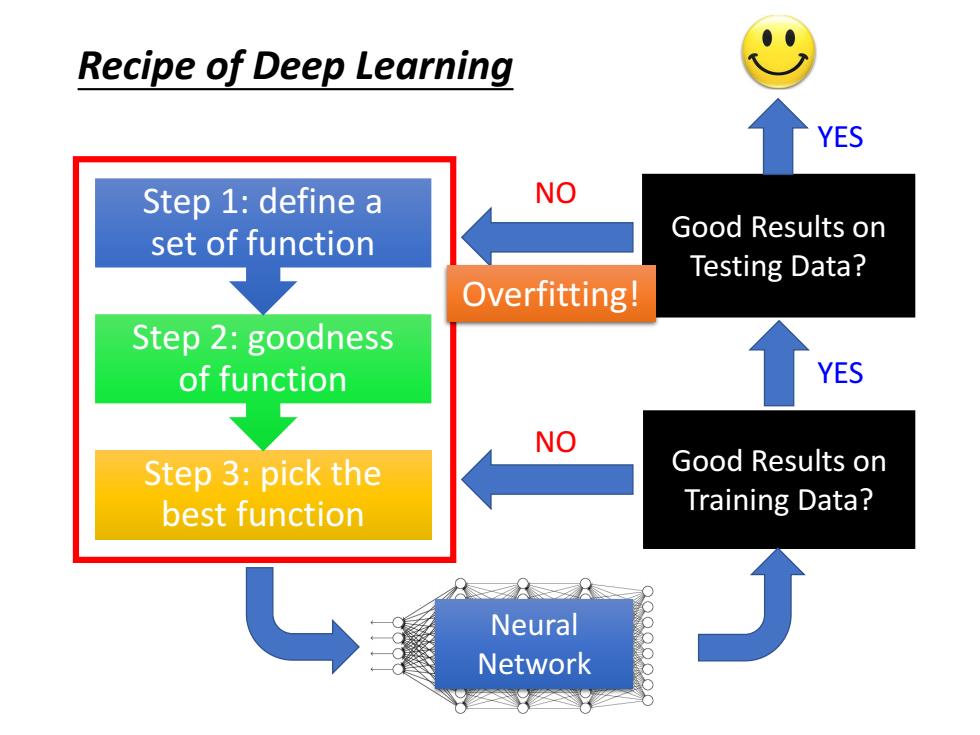
Recipe of Deep Learning YES Step 1:define a NO set of function Good Results on Testing Data? Overfitting! Step 2:goodness of function YES NO Step 3:pick the Good Results on best function Training Data? Neural Network 8
Neural Network Good Results on Testing Data? Good Results on Training Data? Step 3: pick the best function Step 2: goodness of function Step 1: define a set of function YES YES NO NO Overfitting! Recipe of Deep Learning
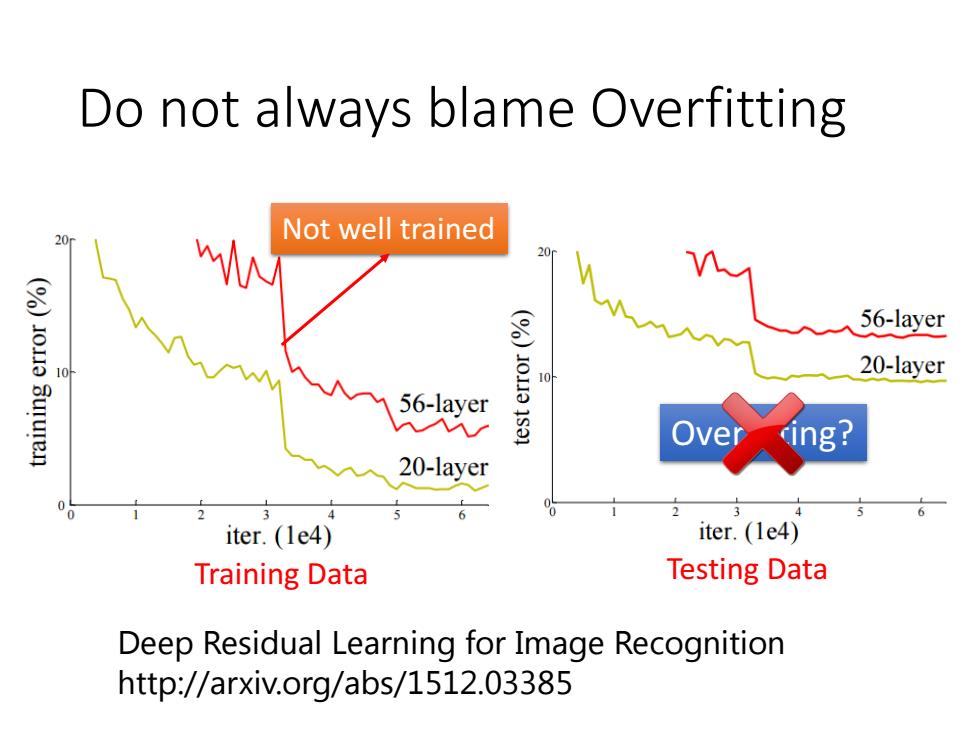
Do not always blame Overfitting Not well trained s 20 (%)I01 Sururen (%)10113 56-layer 10 20-layer 56-layer 密 Over 20-layer 6 iter.(1e4) iter.(1e4) Training Data Testing Data Deep Residual Learning for Image Recognition http://arxiv.org/abs/1512.03385
Do not always blame Overfitting Deep Residual Learning for Image Recognition http://arxiv.org/abs/1512.03385 Testing Data Overfitting? Training Data Not well trained
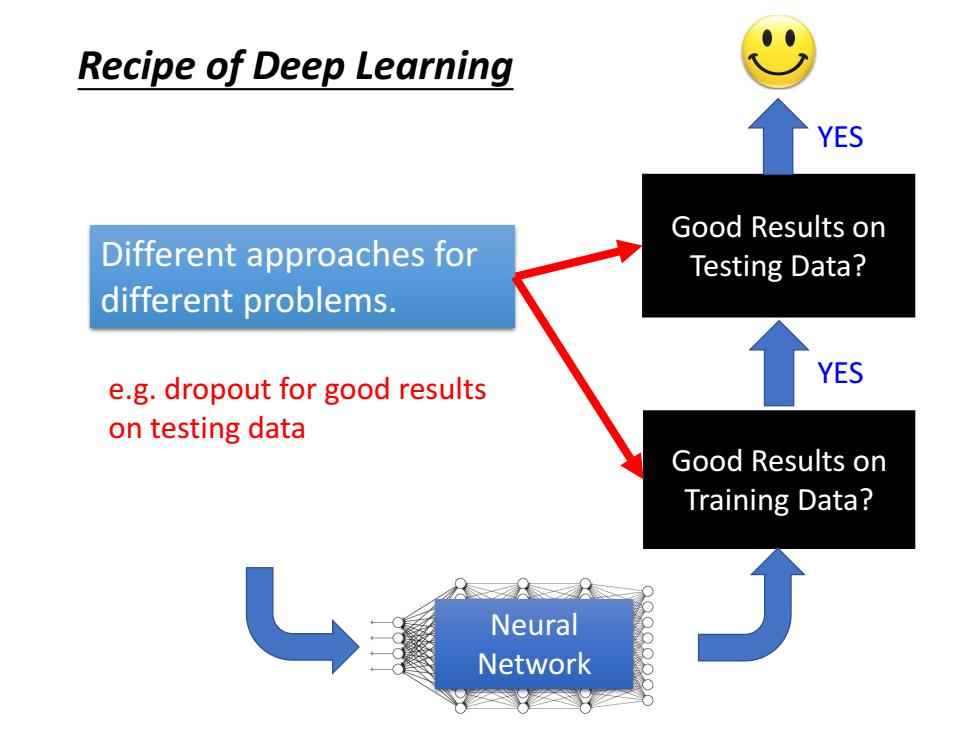
Recipe of Deep Learning YES Good Results on Different approaches for Testing Data? different problems. e.g.dropout for good results YES on testing data Good Results on Training Data? Neural Network
Neural Network Good Results on Testing Data? Good Results on Training Data? YES YES Recipe of Deep Learning Different approaches for different problems. e.g. dropout for good results on testing data
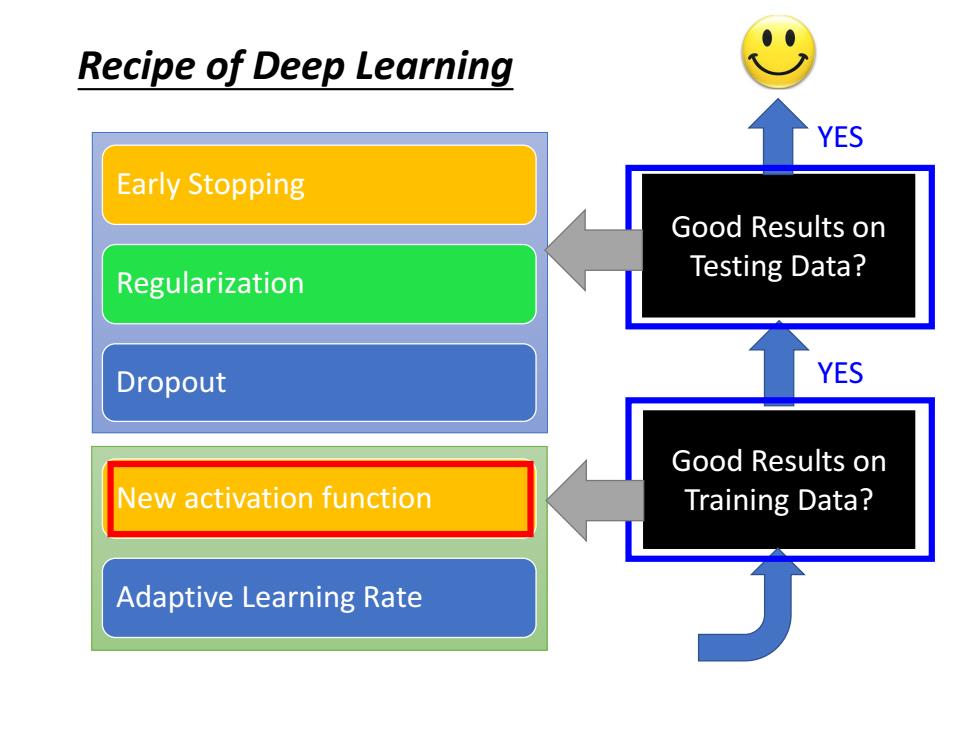
Recipe of Deep Learning YES Early Stopping Good Results on Regularization Testing Data? Dropout YES Good Results on New activation function Training Data? Adaptive Learning Rate
Good Results on Testing Data? Good Results on Training Data? YES YES Recipe of Deep Learning New activation function Adaptive Learning Rate Early Stopping Regularization Dropout
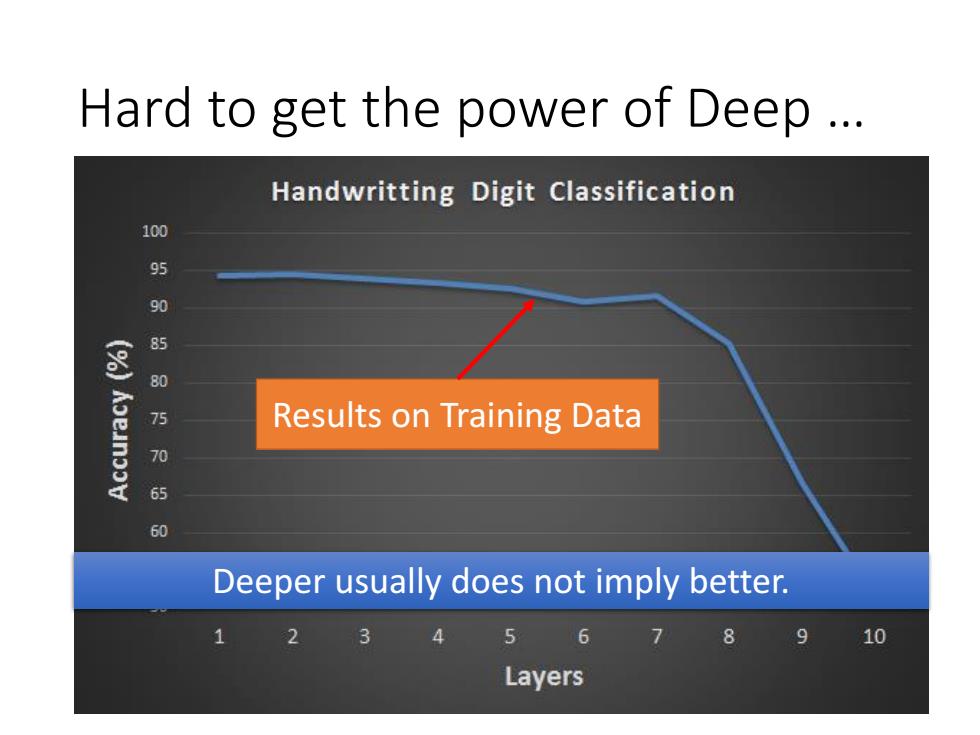
Hard to get the power of Deep .. Handwritting Digit Classification 100 8 90 50万 Results on Training Data 705 60 Deeper usually does not imply better. 2 3 4 5 6 8 910 Layers
Hard to get the power of Deep … Deeper usually does not imply better. Results on Training Data
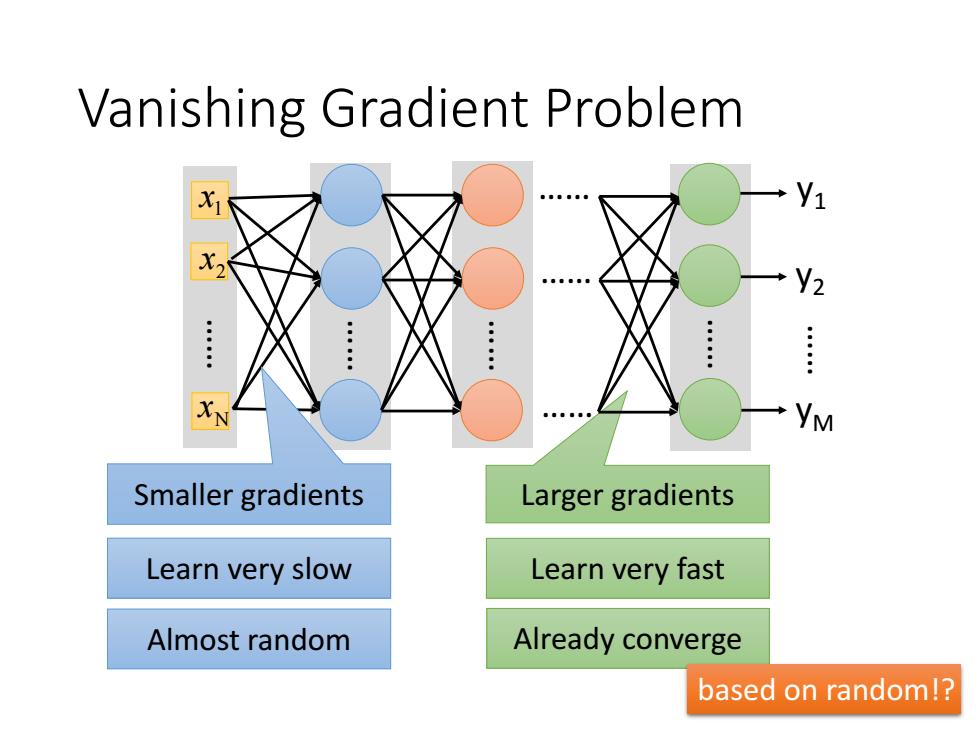
Vanishing Gradient Problem Y1 V2 : YM Smaller gradients Larger gradients Learn very slow Learn very fast Almost random Already converge based on random!?
Vanishing Gradient Problem Larger gradients Almost random Already converge based on random!? Learn very slow Learn very fast 1 x 2 x …… Nx…… …… …… …… …… …… …… y1 y2 yM Smaller gradients
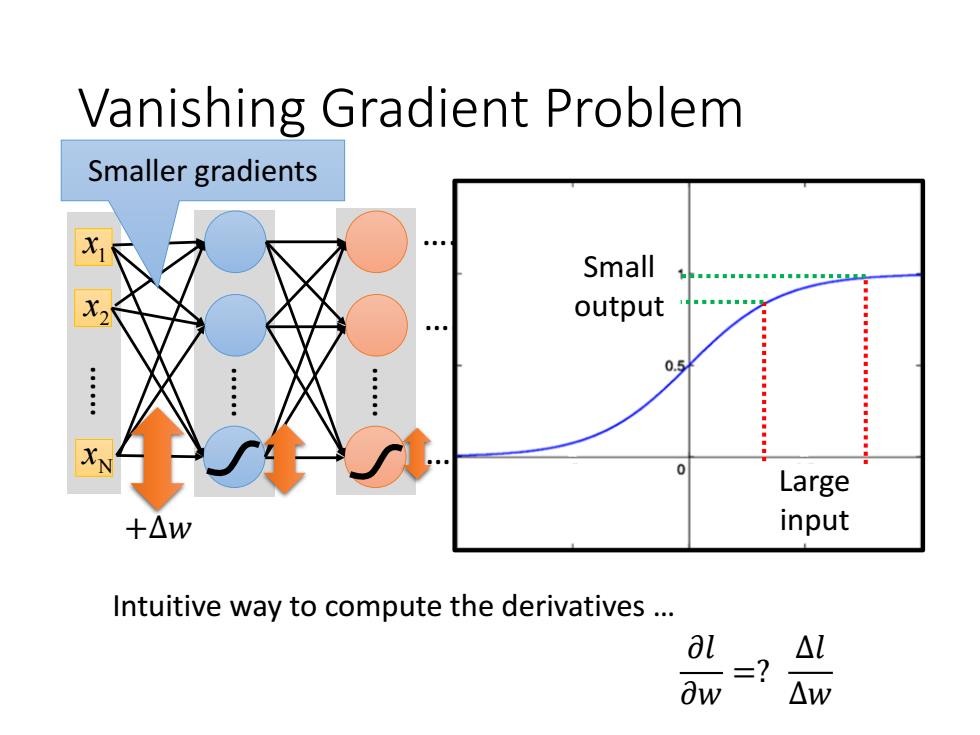
Vanishing Gradient Problem Smaller gradients Small output 0.5 Large +△w input Intuitive way to compute the derivatives .. al △L △W
Vanishing Gradient Problem 1 x 2 x …… Nx…… …… …… …… …… …… …… 𝑦1 𝑦2 𝑦𝑀 …… 𝑦 ො 1 𝑦 ො 2 𝑦 ො 𝑀 𝑙 Intuitive way to compute the derivatives … 𝜕𝑙 𝜕𝑤 =? +∆𝑤 +∆𝑙 ∆𝑙 ∆𝑤 Smaller gradients Large input Small output
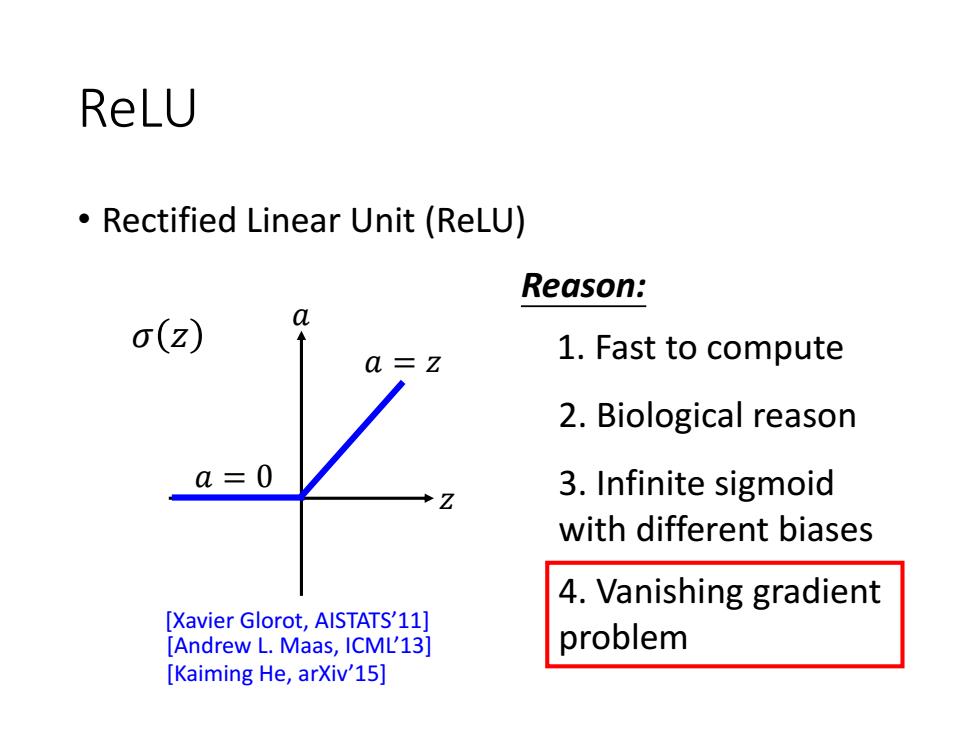
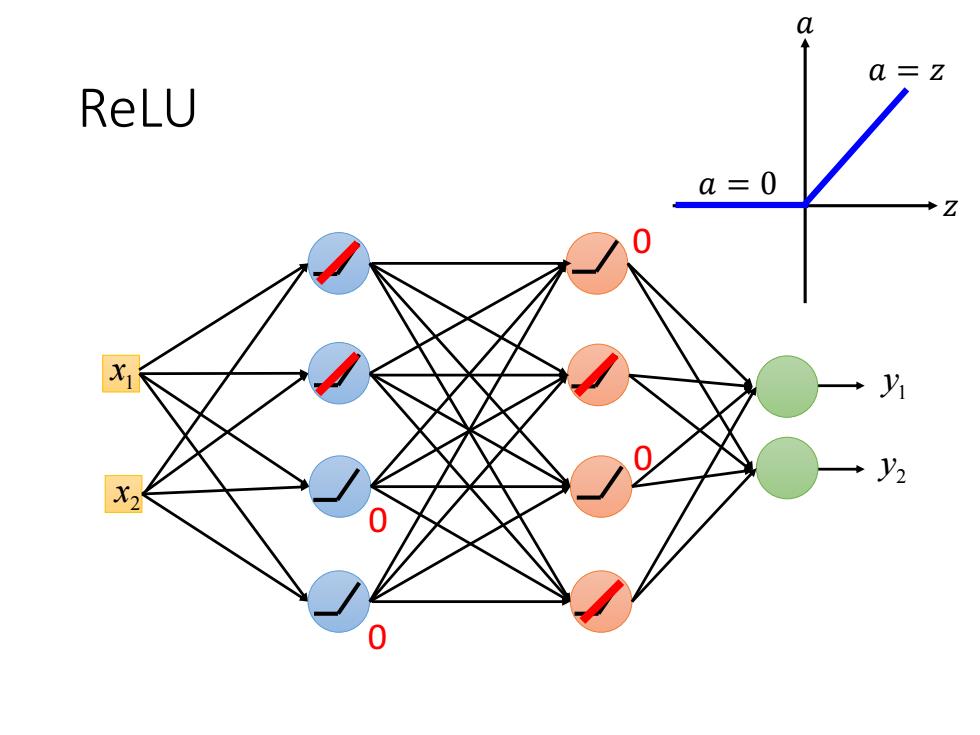
ReLU Rectified Linear Unit (ReLU) Reason: a o(Z) a=z 1.Fast to compute 2.Biological reason a=0 3.Infinite sigmoid with different biases 4.Vanishing gradient [Xavier Glorot,AISTATS'11] [Andrew L.Maas,ICML'13] problem [Kaiming He,arXiv'15]
ReLU • Rectified Linear Unit (ReLU) Reason: 1. Fast to compute 2. Biological reason 3. Infinite sigmoid with different biases 4. Vanishing gradient problem 𝑧 𝑎 𝑎 = 𝑧 𝑎 = 0 𝜎 𝑧 [Xavier Glorot, AISTATS’11] [Andrew L. Maas, ICML’13] [Kaiming He, arXiv’15]
a 三Z ReLU a=0 2 2 X2
ReLU1 x 2 x 1 y2 y 00 00 𝑧 𝑎 𝑎 = 𝑧 𝑎 = 0