
Quick Introduction of Batch Normalization Hung-yi Lee李宏毅 1
Quick Introduction of Batch Normalization Hung-yi Lee 李宏毅 1
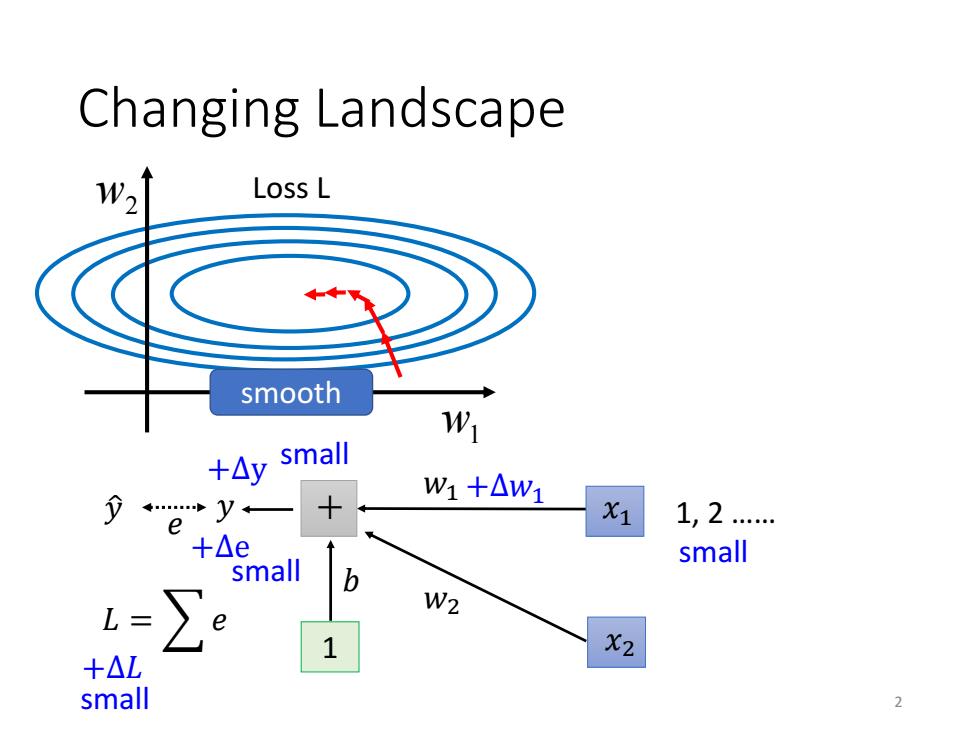
Changing Landscape W2 Loss L smooth W +△y small W1+△W1 e X1 1,2 +△ small mall b L= W2 +△L 1 X2 small 2
Changing Landscape 1 + 1, 2 …… w1 w2 Loss L 𝑦 ො 𝑦 𝑒 𝑏 𝑤1 𝑤2 𝐿 = 𝑒 small 𝑥1 𝑥2 +∆𝑤1 +∆y +∆e +∆𝐿 small smooth small small 2

Changing Landscape Loss L Loss L smooth +△y large W1 y← X1 e 1,2 +△e small same large b L= W2 range △W2 X2 100,200 +△L .s. large large
Changing Landscape 1 + 1, 2 …… 100, 200 …… w1 w2 Loss L w1 w2 Loss L 𝑦 ො 𝑦 𝑒 𝑏 𝑤1 𝑤2 𝐿 = 𝑒 small large 𝑥1 𝑥2 +∆𝑤2 +∆y +∆e +∆𝐿 large smooth steep same range large large 3
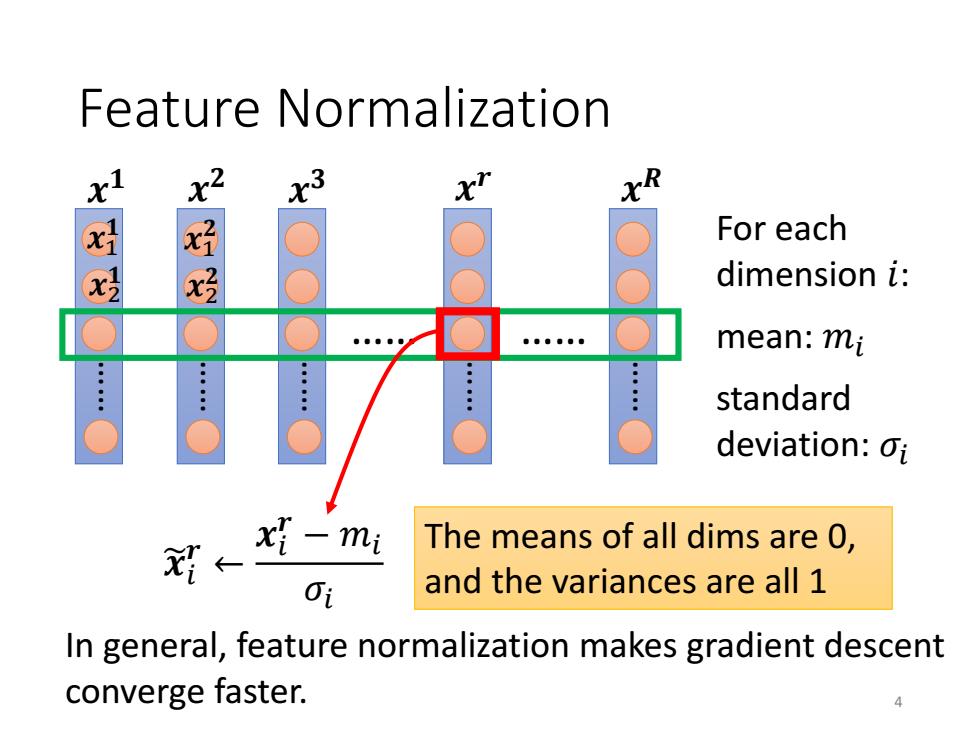
Feature normalization 3 x For each x dimension i: mean:mi : standard deviation:oi x{-mi The means of all dims are 0, ← Oi and the variances are all 1 In general,feature normalization makes gradient descent converge faster. 4
Feature Normalization ……………… …… …… …… …… 𝒙 𝟏 𝒙 𝟐 𝒙 𝟑 𝒙 𝒓 𝒙 𝑹 mean: 𝑚𝑖 standard deviation: 𝜎𝑖 𝒙𝑖 𝒓 ← 𝒙𝑖 𝒓 − 𝑚𝑖 𝜎𝑖 The means of all dims are 0, and the variances are all 1 For each dimension 𝑖: 𝒙1 𝟏 𝒙2 𝟏 𝒙1 𝟐 𝒙2 𝟐 In general, feature normalization makes gradient descent converge faster. 4
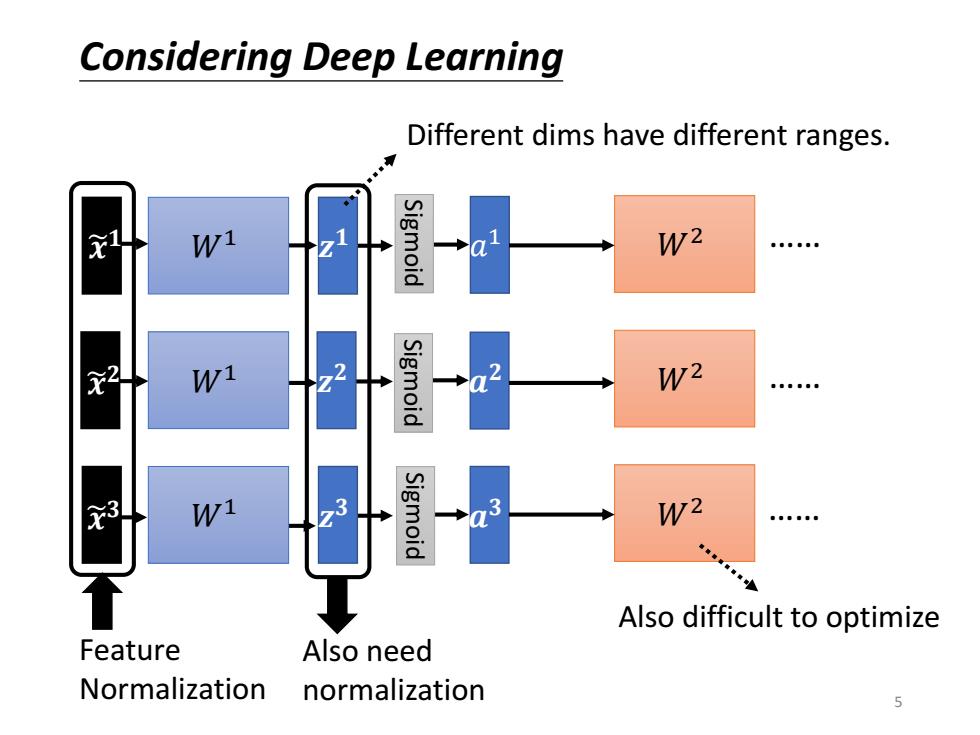
Considering Deep Learning Different dims have different ranges. Wi igmoid W2 元2 W1 Sigmoid W2 。。。。e 3 W1 63 Sigmoid W2 Also difficult to optimize Feature Also need Normalization normalization
𝒂 𝟑 𝒂 𝟐 𝑎 𝑊1 1 𝑊1 𝑊1 𝒛 𝟏 𝒛 𝟐 𝒛 𝟑 𝑊2 𝑊2 𝑊2 Sigmoid …… …… …… Sigmoid Sigmoid Feature Normalization 𝒙 𝟏 𝒙 𝟐 𝒙 𝟑 Also need normalization Different dims have different ranges. Also difficult to optimize Considering Deep Learning 5

Considering Deep Learning 3 Wi 3 W1 ∑a-w2 3 W1 6
𝑊1 𝑊1 𝑊1 𝒛 𝟏 𝒛 𝟐 𝒛 𝟑 𝝁 𝝈 𝝁 = 1 3 𝑖=1 3 𝒛 𝒊 𝝈 = 1 3 𝑖=1 3 𝒛 𝒊 − 𝝁 2 𝒙 𝟏 𝒙 𝟐 𝒙 𝟑 Considering Deep Learning 6

Considering Deep Learning z2-0 This is a large network! G ≌ Wi igmoid Wi 2 22 Sigmoid 3 W1 Sigmoid Consider a batch uand o Batch Normalization depends on zi
𝑊1 𝑊1 𝑊1 𝒛 𝟏 𝒛 𝟐 𝒛 𝟑 𝝁 𝝈 𝒛 𝒊 = 𝒛 𝒊 − 𝝁 𝝈 𝒂 𝟑 𝒂 𝟐 𝒂 𝟏 Sigmoid Sigmoid Sigmoid 𝒛 𝟏 𝒛 𝟐 𝒛 𝟑 This is a large network! 𝒙 𝟏 𝒙 𝟐 𝒙 𝟑 𝝁 and 𝝈 depends on 𝒛 𝒊 Considering Deep Learning Consider a batch Batch Normalization 7 ∆ ∆ ∆ ∆ ∆ ∆ ∆ ∆ ∆
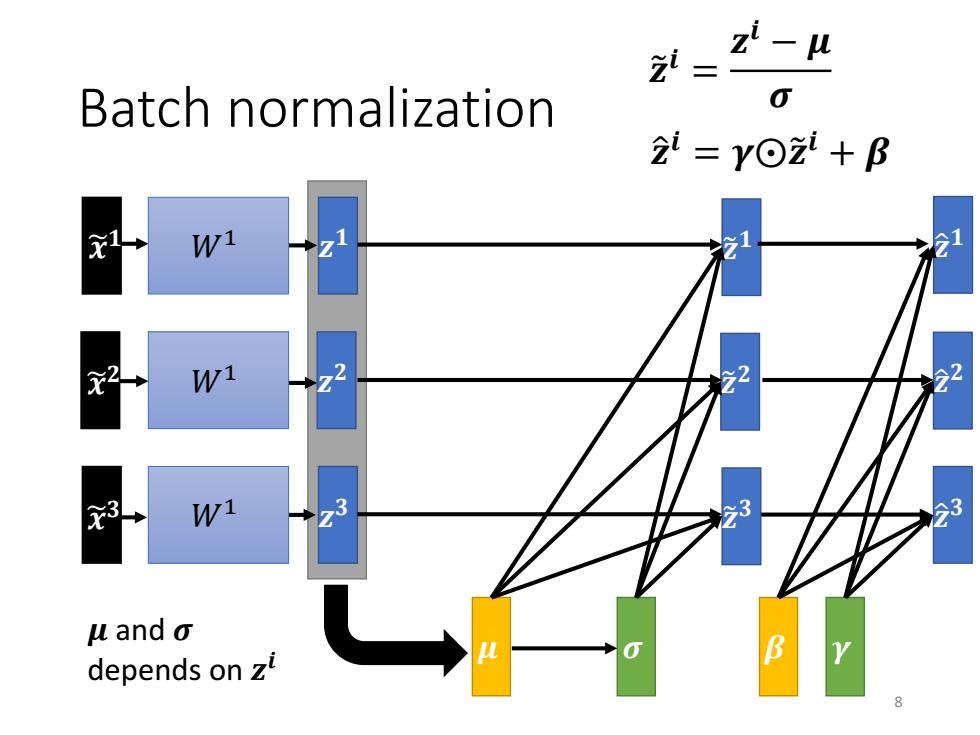
刘、 z2- Batch normalization 0 2=Y⊙z+B W1 W1 2 ≥2 22 3 W1 3 3 63 u and o depends on zt B
Batch normalization 𝑊1 𝑊1 𝑊1 𝒛 𝟏 𝒛 𝟐 𝒛 𝟑 𝝁 𝝈 𝒛 ො 𝒊 = 𝜸⨀𝒛 𝒊 + 𝜷 𝒛 ො 𝟑 𝒛 ො 𝟐 𝒛 ො 𝟏 𝒛 𝟏 𝒛 𝟐 𝒛 𝟑 𝜷 𝜸 𝒛 𝒊 = 𝒛 𝒊 − 𝝁 𝝈 𝝁 and 𝝈 depends on 𝒛 𝒊 𝒙 𝟏 𝒙 𝟐 𝒙 𝟑 8

Batch normalization -Testing i= z-汉 Wi 衣ā Z u,o are from batch? We do not always have batch at testing stage. Computing the moving average of u and o of the batches during training. ul 2 心3 π←pπ+(1-p)u
Batch normalization – Testing 𝒙 𝑊1 𝒛 𝒛 𝒛 = 𝒛 − 𝝁 𝝈 𝝁, 𝝈 are from batch? We do not always have batch at testing stage. Computing the moving average of 𝝁 and 𝝈 of the batches during training. …… 𝝁ഥ 𝝈ഥ 𝝁 𝟏 𝝁 𝟐 𝝁 𝟑 𝝁 …… 𝒕 𝝁ഥ ← 𝑝𝝁ഥ + 1 − 𝑝 𝝁 𝒕
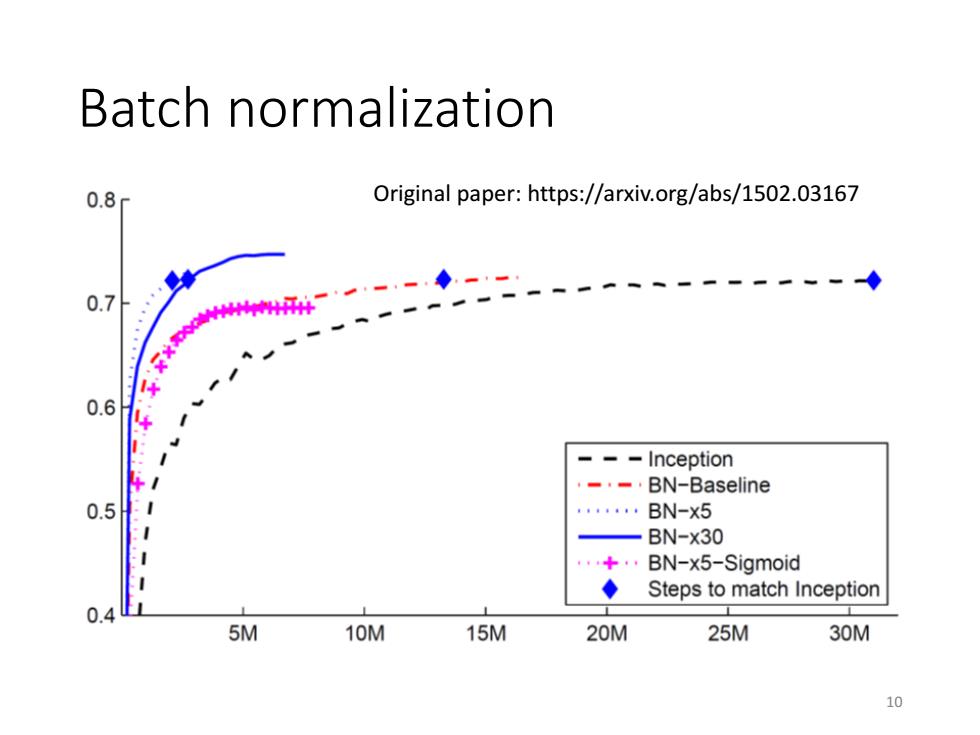
Batch normalization 0.8 Original paper:https://arxiv.org/abs/1502.03167 0.7 0.6 -Inception --BN-Baseline 0.5 ,。。gt,。 BN-x5 BN-x30 BN-x5-Sigmoid ◆ Steps to match Inception 0.4 5M 10M 15M 20M 25M 30M 10
Batch normalization Original paper: https://arxiv.org/abs/1502.03167 10