
Error surface is rugged .. Tips for training:Adaptive Learning Rate
Error surface is rugged … Tips for training: Adaptive Learning Rate 1
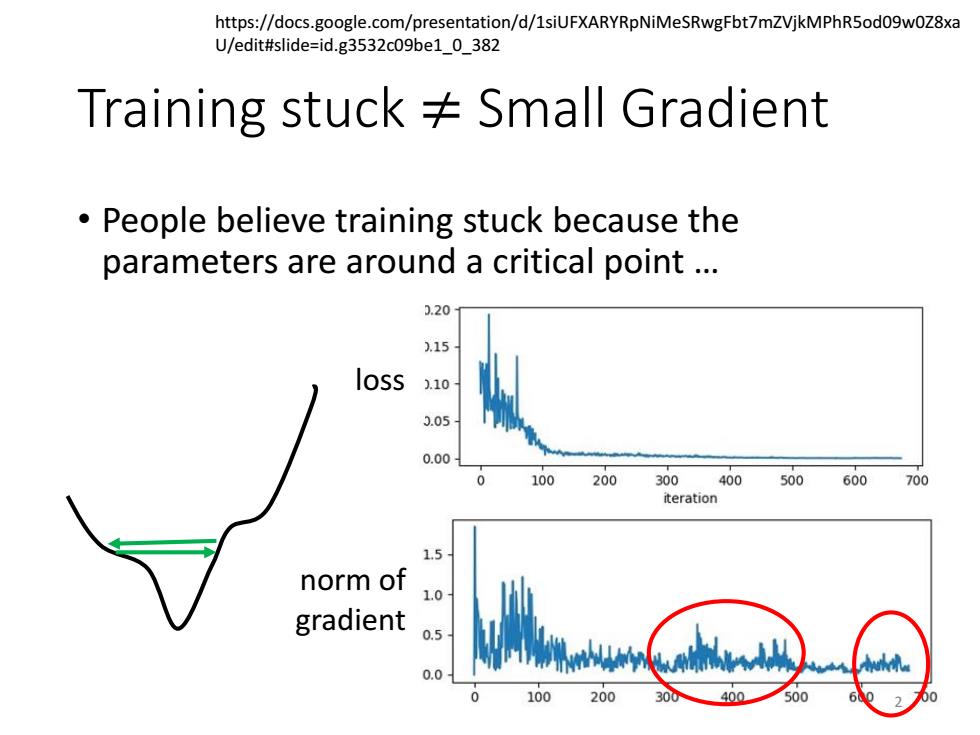
https://docs.google.com/presentation/d/1siUFXARYRpNiMeSRwgFbt7mZVjkMPhR5od09w0Z8xa U/edit#slide=id.g3532c09be1_0_382 Training stuck Small Gradient People believe training stuck because the parameters are around a critical point .. 0.20 .15 loss 1.10 3.05 0.00 100 200 300400500600 700 iteration 1.5 norm of 1.0 gradient 0.5 0.0 100 200 30 400 500
Training stuck ≠ Small Gradient • People believe training stuck because the parameters are around a critical point … loss norm of gradient https://docs.google.com/presentation/d/1siUFXARYRpNiMeSRwgFbt7mZVjkMPhR5od09w0Z8xa U/edit#slide=id.g3532c09be1_0_382 2

Wait a minute... 0.10 0.08 0.06 造o04 0.02 0.00 ·86。 0.0 0.1 0.2 0.3 0.4 0.5 minimum ratio
Wait a minute … 3
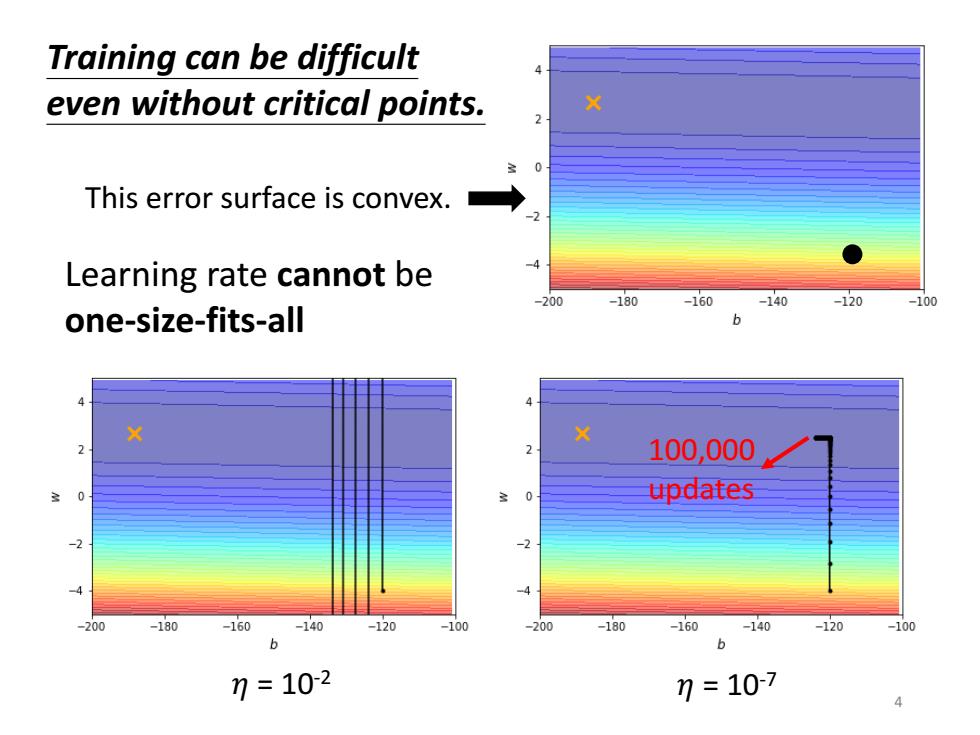
Training can be difficult even without critical points. This error surface is convex. Learning rate cannot be -200 -180 -160 -140 -120 -100 one-size-fits-all 6 X 100,000 0 updates 200 -180 -160 -140 -120 -100 -200 -180 -160 -140 -120 -100 b b 7=102 7=107 4
100,000 updates 𝜂 = 10-2 Learning rate cannot be one-size-fits-all Training can be difficult even without critical points. 𝜂 = 10-7 4 This error surface is convex
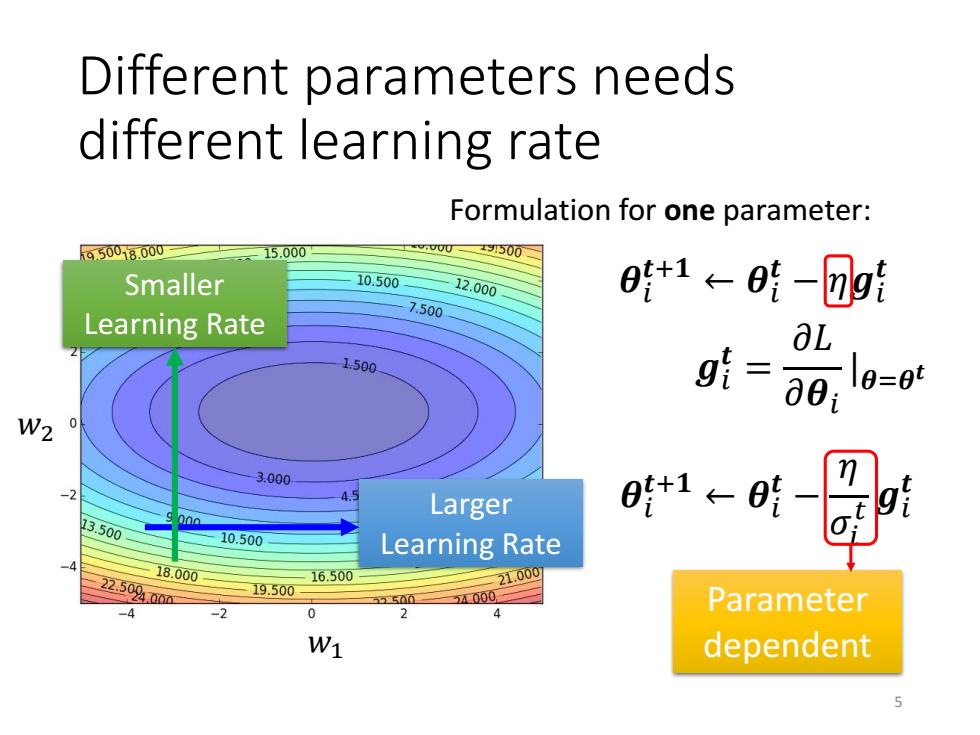
Different parameters needs different learning rate Formulation for one parameter: 650018.000 15.000 x3500 Smaller 10.500 12.000 0+1←01-⑦g1 7.500 Learning Rate aL 1500 g1=∂01 0=09 W2 0 3.000 Larger 时t1←时 13.500 00a 10.500 Learning Rate 18.000 22.50400m 16.500 19.500 21.000 5000 Parameter dependent
Different parameters needs different learning rate 𝑤1 𝑤2 Larger Learning Rate Smaller Learning Rate 𝜽𝑖 𝒕+𝟏 ← 𝜽𝑖 𝒕 − 𝜂𝒈𝑖 𝒕 𝜽𝑖 𝒕+𝟏 ← 𝜽𝑖 𝒕 − 𝜂 𝜎𝑖 𝑡 𝒈𝑖 𝒕 Parameter dependent 𝒈𝑖 𝒕 = 𝜕𝐿 𝜕𝜽𝑖 |𝜽=𝜽 𝒕 Formulation for one parameter: 5
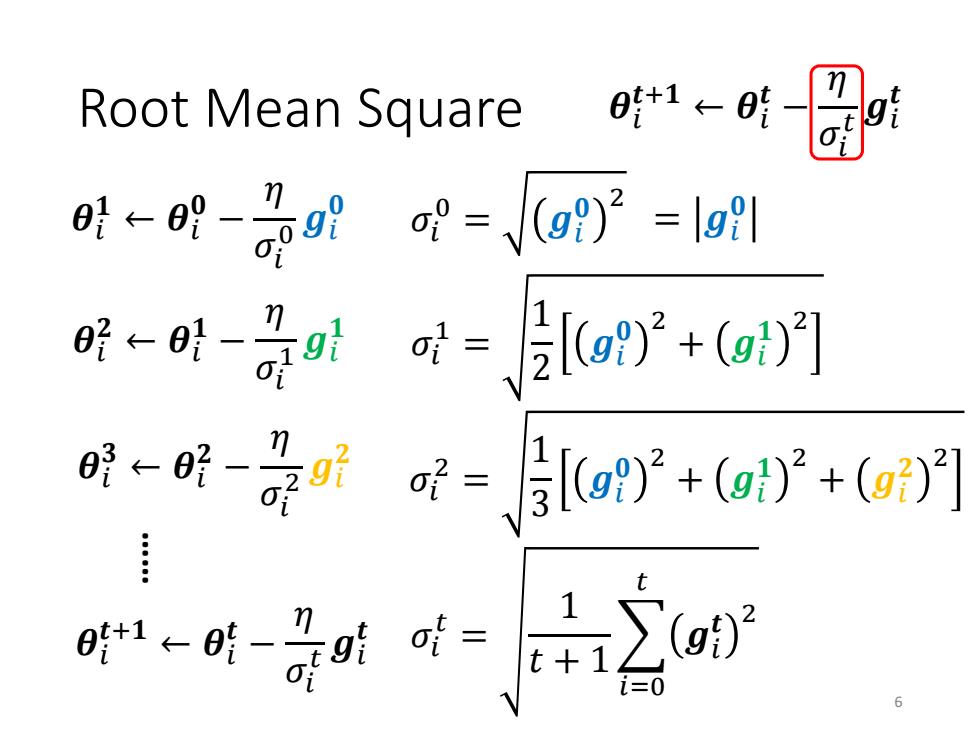
Root Mean Square 时←明-是a时-o-l n a脱←a}- =2g+()] 0←- n =g92+(2+(g)1 0+1← -71 6
Root Mean Square 𝜎𝑖 0 = 𝒈𝑖 𝟎 2 𝜎𝑖 1 = 1 2 𝒈𝑖 𝟎 2 + 𝒈𝑖 𝟏 2 𝜎𝑖 𝑡 = 1 𝑡 + 1 𝑖=0 𝑡 𝒈𝑖 𝒕 2 𝜎𝑖 2 = 1 3 𝒈𝑖 𝟎 2 + 𝒈𝑖 𝟏 2 + 𝒈𝑖 𝟐 2 𝜽𝑖 𝟏 ← 𝜽𝑖 𝟎 − 𝜂 𝜎𝑖 0 𝒈𝑖 𝟎 𝜽𝑖 𝒕+𝟏 ← 𝜽𝑖 𝒕 − 𝜂 𝜎𝑖 𝑡 𝒈𝑖 𝒕 𝜽𝑖 𝟐 ← 𝜽𝑖 𝟏 − 𝜂 𝜎𝑖 1 𝒈𝑖 𝟏 𝜽𝑖 𝟑 ← 𝜽𝑖 𝟐 − 𝜂 𝜎𝑖 2 𝒈𝑖 𝟐 𝜽𝑖 𝒕+𝟏 ← 𝜽𝑖 𝒕 − 𝜂 𝜎𝑖 𝑡 𝒈𝑖 𝒕 …… 6 = 𝒈𝑖 𝟎
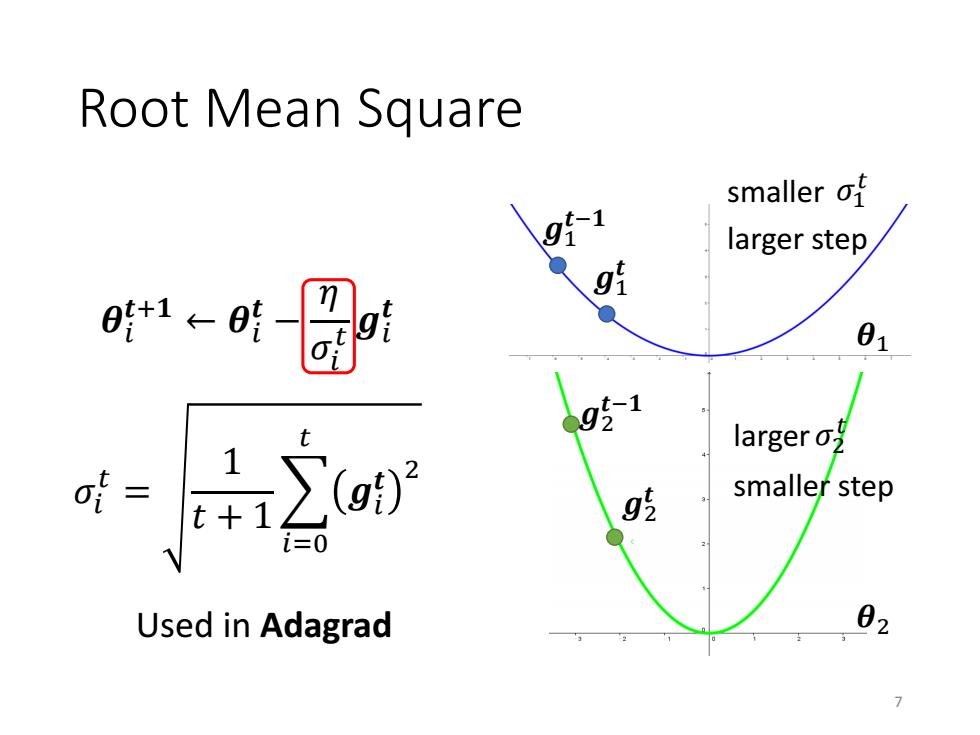
Root mean square 9f1 smaller of larger step gl 01 g51 larger g smaller step i=0 Used in Adagrad 02 7
Root Mean Square 𝜎𝑖 𝑡 = 1 𝑡 + 1 𝑖=0 𝑡 𝒈𝑖 𝒕 2 𝜽𝑖 𝒕+𝟏 ← 𝜽𝑖 𝒕 − 𝜂 𝜎𝑖 𝑡 𝒈𝑖 𝒕 𝜽1 𝜽2 𝒈1 𝒕−𝟏 𝒈1 𝒕 𝒈2 𝒕−𝟏 𝒈2 𝒕 smaller 𝜎1 𝑡 larger𝜎2 𝑡 larger step smaller step Used in Adagrad 7
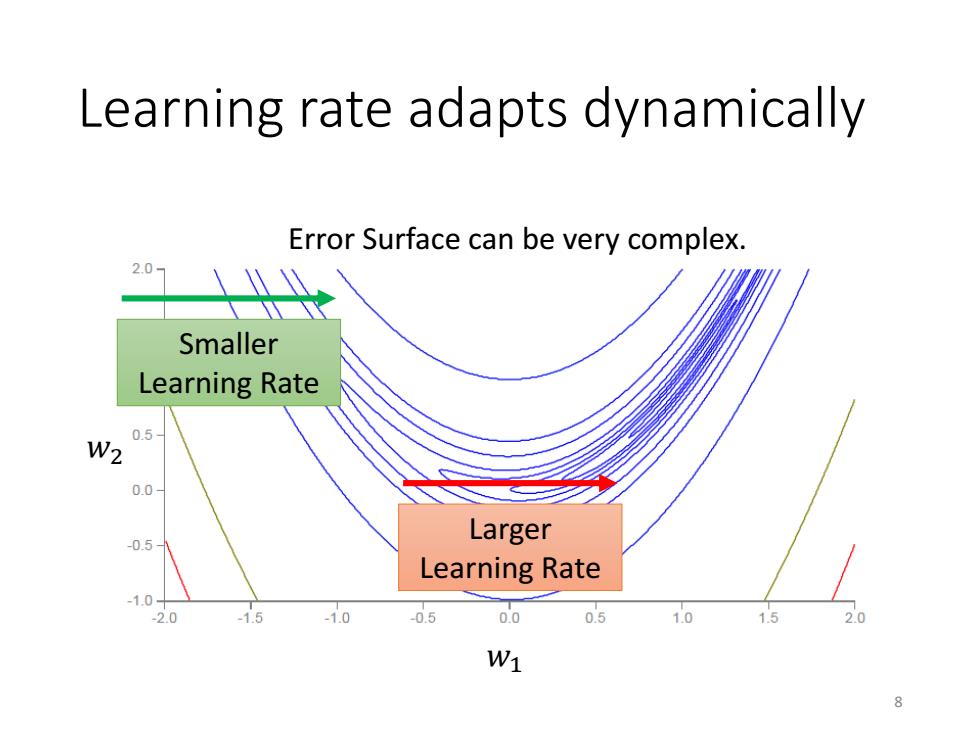
Learning rate adapts dynamically Error Surface can be very complex. Smaller Learning Rate 0.5 W2 0.0 -0.5 Larger Learning Rate -10 2.0 1.5 -1.0 0.5 0.0 0.5 1.0 1.5 W1 8
Learning rate adapts dynamically 𝑤1 𝑤2 Error Surface can be very complex. Larger Learning Rate Smaller Learning Rate 8
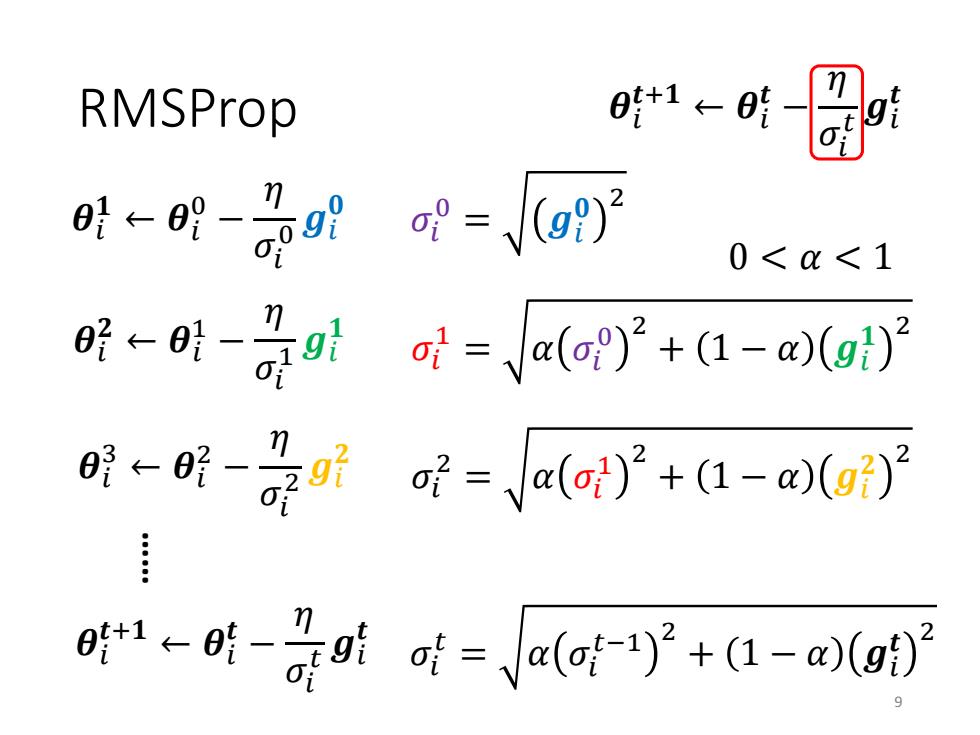
RMSProp 41←明9 0<<1 o=Va(o)2+(1-a(gi)2 0明←-2听=Va(}'+1-a(g) a1←时-是0时时-(a时-y+1-o
RMSProp 𝜎𝑖 0 = 𝒈𝑖 𝟎 2 𝜎𝑖 1 = 𝛼 𝜎𝑖 0 2 + 1 − 𝛼 𝒈𝑖 𝟏 2 𝜎𝑖 𝑡 = 𝛼 𝜎𝑖 𝑡−1 2 + 1 − 𝛼 𝒈𝑖 𝒕 2 𝜎𝑖 2 = 𝛼 𝜎𝑖 1 2 + 1 − 𝛼 𝒈𝑖 𝟐 2 𝜽𝑖 𝟏 ← 𝜽𝑖 0 − 𝜂 𝜎𝑖 0 𝒈𝑖 𝟎 𝜽𝑖 𝒕+𝟏 ← 𝜽𝑖 𝒕 − 𝜂 𝜎𝑖 𝑡 𝒈𝑖 𝒕 𝜽𝑖 𝟐 ← 𝜽𝑖 1 − 𝜂 𝜎𝑖 1 𝒈𝑖 𝟏 𝜽𝑖 3 ← 𝜽𝑖 2 − 𝜂 𝜎𝑖 2 𝒈𝑖 𝟐 𝜽𝑖 𝒕+𝟏 ← 𝜽𝑖 𝒕 − 𝜂 𝜎𝑖 𝑡 𝒈𝑖 𝒕 …… 0 < 𝛼 < 1 9

RMSProp g}g1…g51 0<0<1 1←时圆a=、aa-yP+1-wa The recent gradient has larger influence, and the past gradients have less influence. small of increase of larger step smaller step decrease of larger step 10
RMSProp 𝜽𝑖 𝒕+𝟏 ← 𝜽𝑖 𝒕 − 𝜂 𝜎𝑖 𝑡 𝒈𝑖 𝒕 increase 𝜎𝑖 𝑡 decrease 𝜎𝑖 𝑡 smaller step larger step 𝜎𝑖 𝑡 = 𝛼 𝜎𝑖 𝑡−1 2 + 1 − 𝛼 𝒈𝑖 𝒕 2 0 < 𝛼 < 1 The recent gradient has larger influence, and the past gradients have less influence. small 𝜎𝑖 𝑡 larger step 10 𝒈𝑖 𝟏 𝒈𝑖 𝟐 …… 𝒈𝑖 𝒕−𝟏