
Unsupervised Learning: Principle Component Analysis
Unsupervised Learning: Principle Component Analysis

Unsupervised Learning ● Dimension Reduction ·Generation(無中生有) (化繁為簡) only having function input function only having function output function Random numbers
Unsupervised Learning • Dimension Reduction (化繁為簡) • Generation (無中生有) function function Random numbers only having function input only having function output
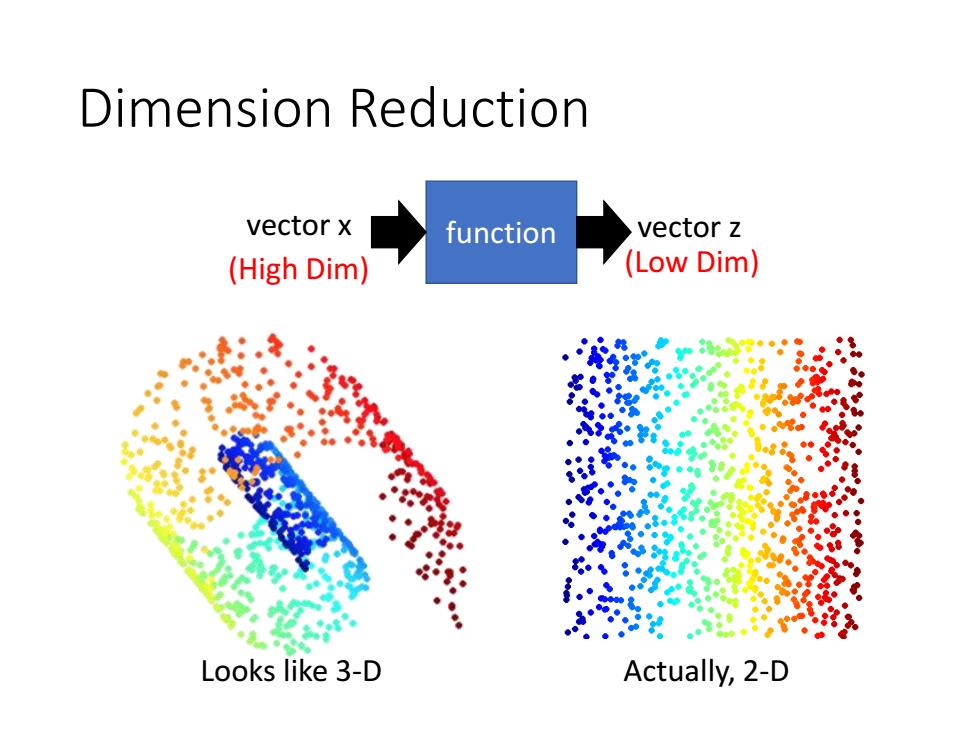
Dimension Reduction vector x function vector z (High Dim) (Low Dim) Looks like 3-D Actually,2-D
Dimension Reduction Looks like 3-D Actually, 2-D function vector x vector z (High Dim) (Low Dim)
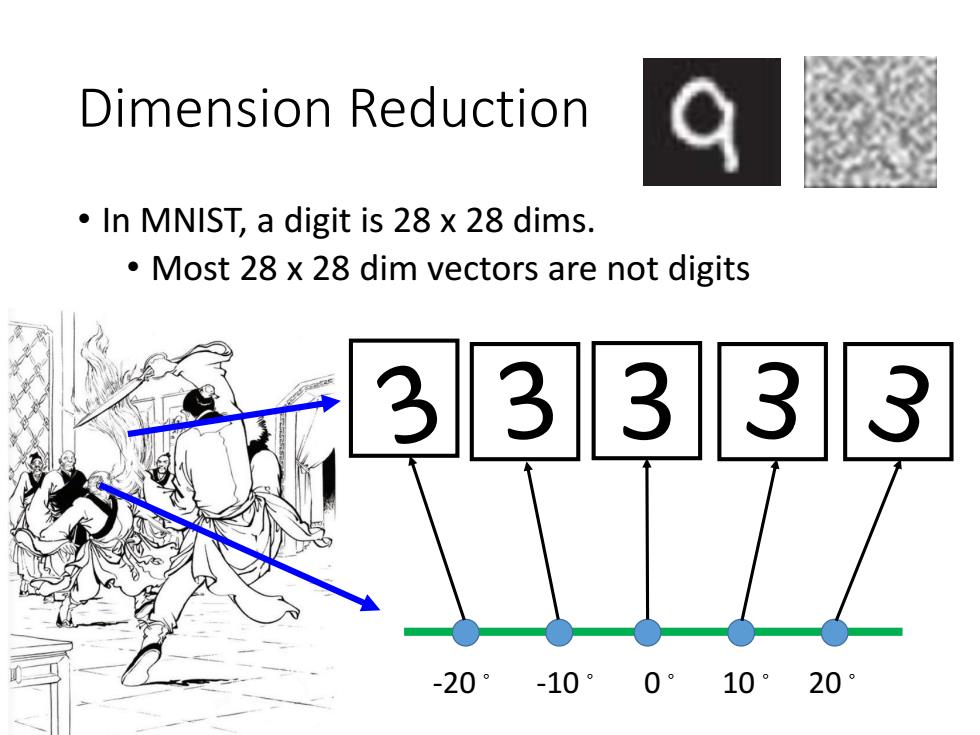
Dimension Reduction In MNIST,a digit is 28 x 28 dims. Most 28 x 28 dim vectors are not digits 3 333 -20°-10° 0°10°20°
Dimension Reduction • In MNIST, a digit is 28 x 28 dims. • Most 28 x 28 dim vectors are not digits 3 -20。 -10。 0。 10。 20
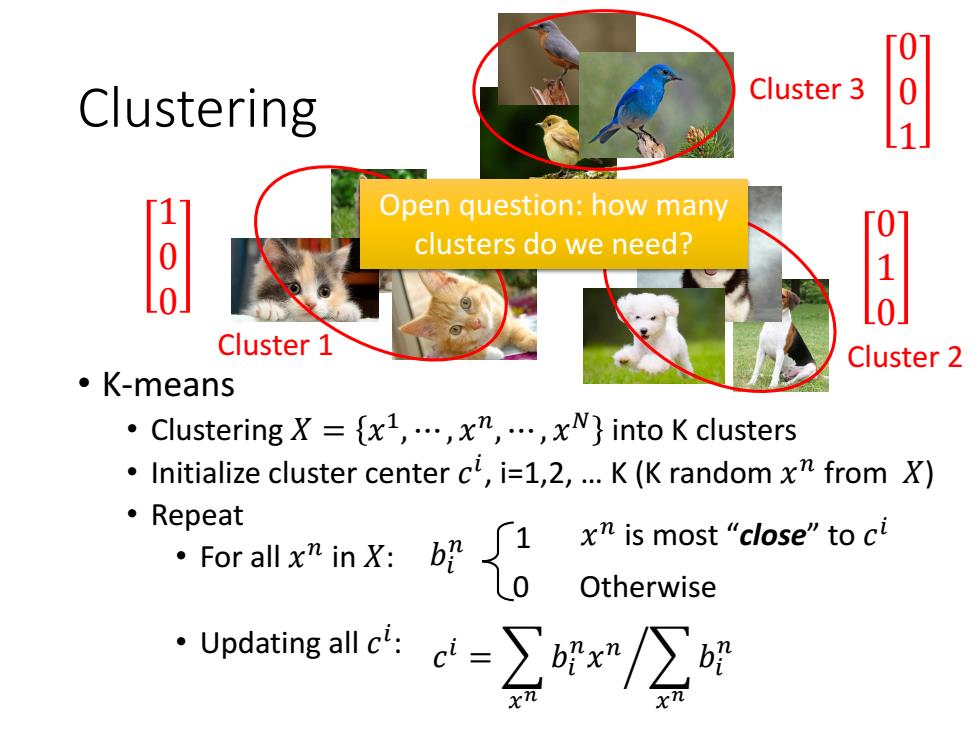
0 Clustering Cluster 3 0 1 Open question:how many 8 clusters do we need? Cluster 1 Cluster 2 。K-means ·Clustering X={xl,…,xn,,xN}into K clusters Initialize cluster center cl,i=1,2,...K (K random x from X) 。Repeat nX好0 x is most "close"to ci Otherwise ·Updating4c=∑oix/∑时
Clustering • K-means • Clustering 𝑋 = 𝑥 1 , ⋯ , 𝑥 𝑛 , ⋯ , 𝑥 𝑁 into K clusters • Initialize cluster center 𝑐 𝑖 , i=1,2, … K (K random 𝑥 𝑛 from 𝑋) • Repeat • For all 𝑥 𝑛 in 𝑋: • Updating all 𝑐 𝑖 : Cluster 1 Cluster 2 Cluster 3 Open question: how many clusters do we need? 𝑏𝑖 𝑛 0 1 𝑐 𝑖 = ൘ 𝑥 𝑛 𝑏𝑖 𝑛 𝑥 𝑛 𝑥 𝑛 𝑏𝑖 𝑛 Otherwise 𝑥 𝑛 is most “close” to 𝑐 𝑖 1 0 0 0 1 0 0 0 1
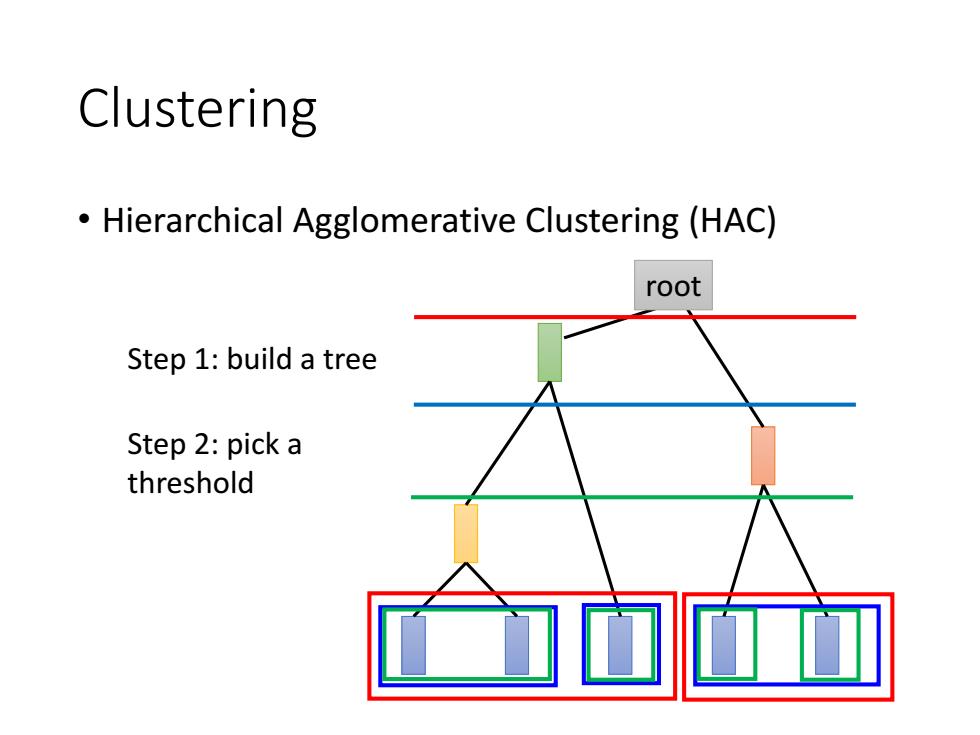
Clustering Hierarchical Agglomerative Clustering (HAC) root Step 1:build a tree Step 2:pick a threshold
Clustering • Hierarchical Agglomerative Clustering (HAC) Step 1: build a tree Step 2: pick a threshold root
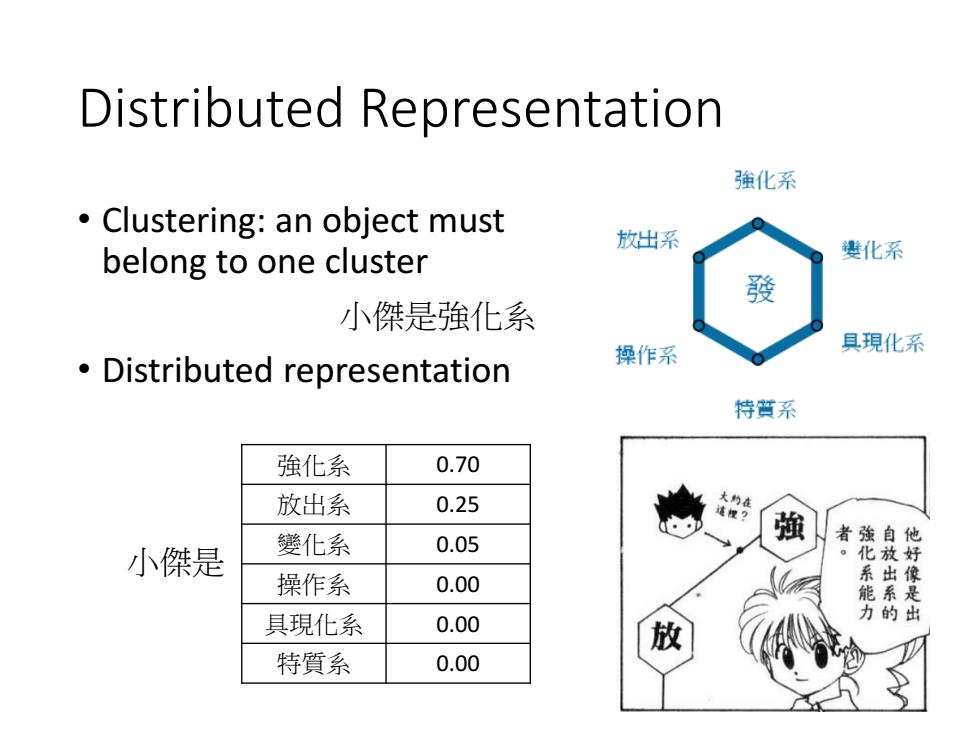
Distributed Representation 強化系 Clustering:an object must 放出系 belong to one cluster 贵化系 發 小傑是強化系 具現化系 Distributed representation 操作系 特質系 強化系 0.70 放出系 0.25 變化系 強 0.05 者強自 他 小傑是 化系能力 操作系 0.00 具現化系 0.00 特質系 0.00
Distributed Representation • Clustering: an object must belong to one cluster • Distributed representation 小傑是強化系 小傑是 強化系 0.70 放出系 0.25 變化系 0.05 操作系 0.00 具現化系 0.00 特質系 0.00
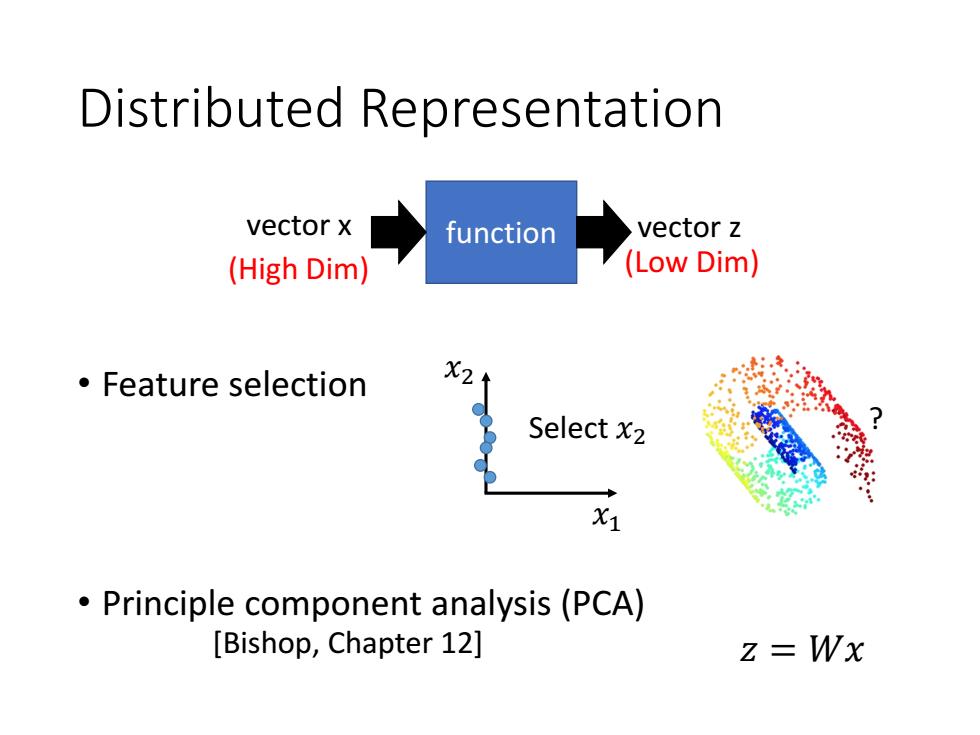
Distributed Representation vector x function vector z (High Dim) (Low Dim) 。Feature selection X2 Select x2 X1 Principle component analysis (PCA) [Bishop,Chapter 12] z=Wx
Distributed Representation • Feature selection • Principle component analysis (PCA) ? 𝑥1 𝑥2 Select 𝑥2 [Bishop, Chapter 12] 𝑧 = 𝑊𝑥 function vector x vector z (High Dim) (Low Dim)
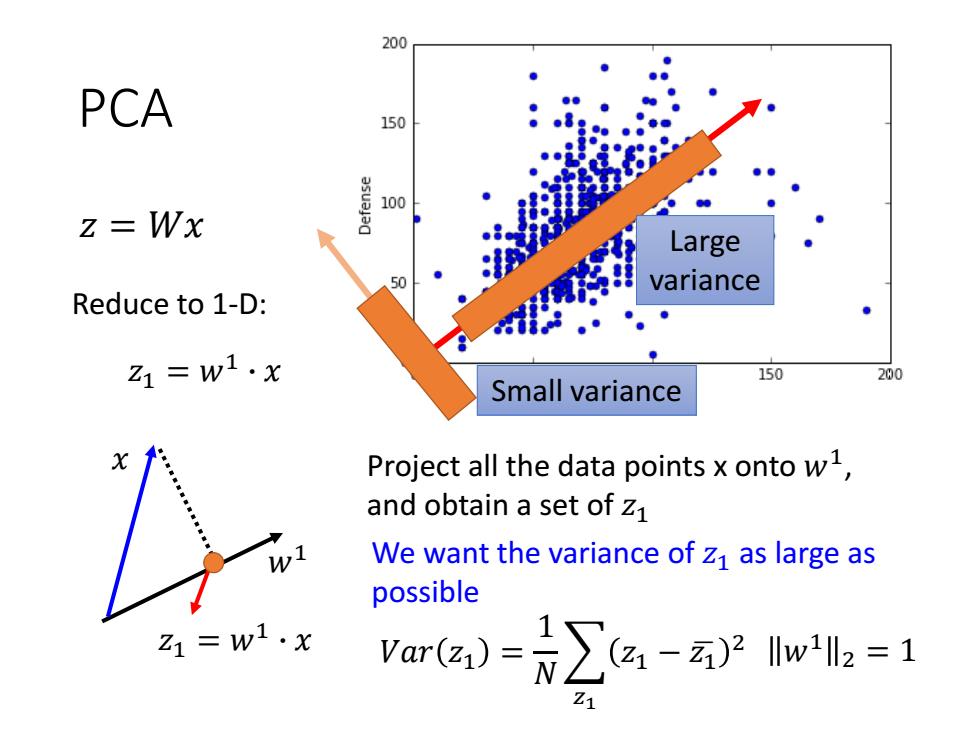
200 PCA 150 100 z=Wx Large So variance Reduce to 1-D: 1=w1·x 150 200 Small variance Project all the data points x onto w1, and obtain a set of Z1 We want the variance of z1 as large as possible =w1·x are)-∑a-we=1
PCA 𝑤1 𝑥 Project all the data points x onto 𝑤1 , and obtain a set of 𝑧1 We want the variance of 𝑧1 as large as possible Large variance Small variance 𝑉𝑎𝑟 𝑧1 = 1 𝑁 𝑧1 𝑧1 − 𝑧ഥ1 2 𝑧 = 𝑊𝑥 𝑧1 = 𝑤1 ∙ 𝑥 𝑧1 = 𝑤1 ∙ 𝑥 Reduce to 1-D: 𝑤1 2 = 1
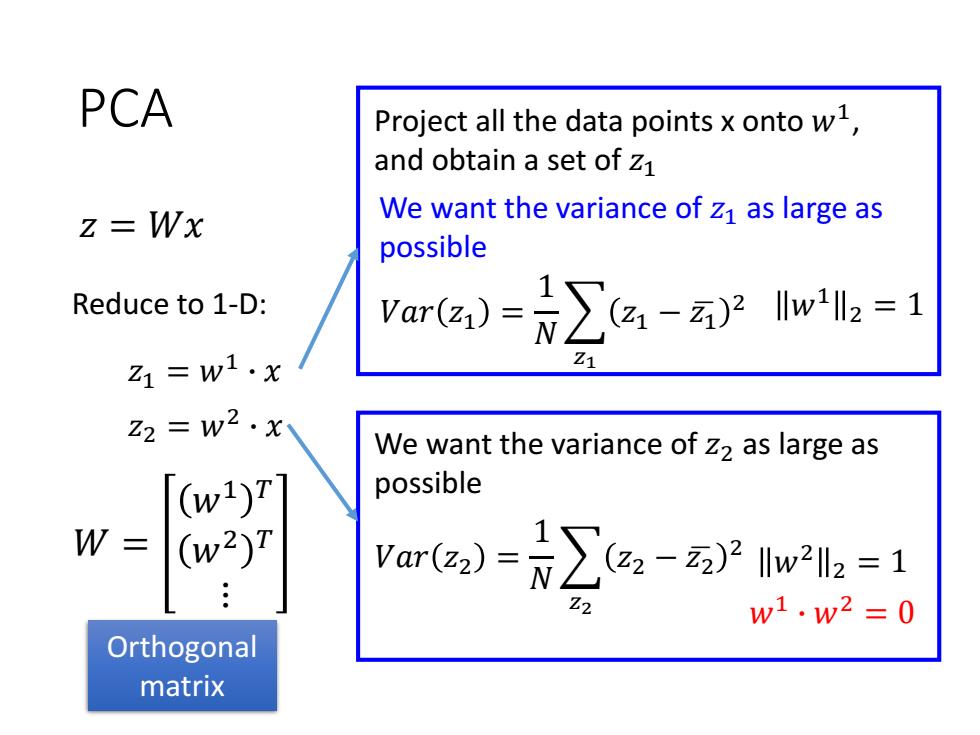
PCA Project all the data points x onto w1, and obtain a set of z1 z=Wx We want the variance of z1 as large as possible Reduce to 1-D: Vare)=∑a-a2w2=1 Z1=w1·x Z1 Z2 w2.x We want the variance of z2 as large as [(w1)T possible W = (w2)T var(z)=∑a,-a2w2l2=1 w1w2=0 Orthogonal matrix
PCA We want the variance of 𝑧2 as large as possible 𝑉𝑎𝑟 𝑧2 = 1 𝑁 𝑧2 𝑧2 − 𝑧ഥ2 2 𝑤2 2 = 1 𝑤1 ∙ 𝑤2 = 0 𝑧 = 𝑊𝑥 𝑧1 = 𝑤1 ∙ 𝑥 Reduce to 1-D: Project all the data points x onto 𝑤1 , and obtain a set of 𝑧1 We want the variance of 𝑧1 as large as possible 𝑉𝑎𝑟 𝑧1 = 1 𝑁 𝑧1 𝑧1 − 𝑧ഥ1 2 𝑤1 2 = 1 𝑧2 = 𝑤2 ∙ 𝑥 𝑊 = 𝑤1 𝑇 𝑤2 𝑇 ⋮ Orthogonal matrix