
《数学分析川》教学大纲 课程编码:1512100606 课程名称:数学分析Ⅱ 学时/学分:96/6 先修课程:《数学分析I》 适用专业:信总与计算科学 开课教研室:分析与方程教研室 一、课程性质与任务 课程性质:《数学分析(Ⅱ)》是信息与计算科学专业的一门重要的专业基础课程.研究 的主要内容是如何求解不定积分和定积分,如何理解和讨论级数和反常积分的敛散性,它是 分析数学系列课程之一,也是其他后继课程的重要基础。在第2学期开设。 课程任务:掌握导数的应用、不定积分的概念、计算方法,掌握定积分的概念、可积条 件、计算方法及几何意义、定积分的几何应用和物理应用:反常积分和级数敛散的概念和敛 散性的基本判别方法及幂级数的基本知识:初步培养具有用定积分解决实际问题的能力和敛 散性的思想,为后继课程的学习打好必要的基础知识。开设本课程的目的是培养学生具有抽 象思维能力、逻辑推理能力、空间想象能力、运算能力和综合运用所学的知识分析和解决问 愿的能力。通过系统的学习与严格的训练,使学生全面掌握数学分析中的积分理论、级数理 论知识:提高建立数学模型并应用积分理论、级数理论这些工具解决实际应用间题的能力。 二、课程教学基本要求 掌握微分中值定理和导师的应用,掌握不定积分的概念与运算法则,熟练应用换元法和 分部积分法求解不定积分,掌握求有理函数与部分无理函数不定积分的方法。理解定积分的 概念,牢周掌握微积分基本定理:牛顿一莱布尼兹公式用于定积分的计算,熟练运用微元法 解决几何,物理中的实际问题,初步掌握定积分的数值计算。掌握反常积分的概念,熟练掌 握反常积分的收敛判别法与反常积分的计算。掌握数项级数敛散性的概念,熟练运用各种判 别法判别正项级数,任意项级数与无穷乘积的敛散性。掌握函数项级数(函数序列)一致收 敛性概念,一致收敛性的判别法与一致收敛级数的性质,掌握幂级数的性质,会熟练展开函 数为幂级数,了解函数的幂级数展开的重要应用。 成绩考核形式为考试成绩考核形式:末考成绩(闭卷考试)(70%)+平时成绩(作业、 课堂提问、课堂讨论等)(30%)。成绩评定采用百分制,60分为及格。 三、课程教学内容 第六章 微分中值定理及其应用 1.教学基本要求
《数学分析Ⅱ》教学大纲 课程编码:1512100606 课程名称:数学分析Ⅱ 学时/学分:96/6 先修课程:《数学分析Ⅰ》 适用专业:信息与计算科学 开课教研室:分析与方程教研室 一、课程性质与任务 课程性质:《数学分析(Ⅱ)》是信息与计算科学专业的一门重要的专业基础课程.研究 的主要内容是如何求解不定积分和定积分,如何理解和讨论级数和反常积分的敛散性,它是 分析数学系列课程之一,也是其他后继课程的重要基础。在第 2 学期开设。 课程任务:掌握导数的应用、不定积分的概念、计算方法,掌握定积分的概念、可积条 件、计算方法及几何意义、定积分的几何应用和物理应用;反常积分和级数敛散的概念和敛 散性的基本判别方法及幂级数的基本知识;初步培养具有用定积分解决实际问题的能力和敛 散性的思想,为后继课程的学习打好必要的基础知识。开设本课程的目的是培养学生具有抽 象思维能力、逻辑推理能力、空间想象能力、运算能力和综合运用所学的知识分析和解决问 题的能力。通过系统的学习与严格的训练,使学生全面掌握数学分析中的积分理论、级数理 论知识;提高建立数学模型并应用积分理论、级数理论这些工具解决实际应用问题的能力。 二、课程教学基本要求 掌握微分中值定理和导师的应用,掌握不定积分的概念与运算法则,熟练应用换元法和 分部积分法求解不定积分,掌握求有理函数与部分无理函数不定积分的方法。理解定积分的 概念,牢固掌握微积分基本定理:牛顿—莱布尼兹公式用于定积分的计算,熟练运用微元法 解决几何,物理中的实际问题,初步掌握定积分的数值计算。掌握反常积分的概念,熟练掌 握反常积分的收敛判别法与反常积分的计算。掌握数项级数敛散性的概念,熟练运用各种判 别法判别正项级数,任意项级数与无穷乘积的敛散性。掌握函数项级数(函数序列)一致收 敛性概念,一致收敛性的判别法与一致收敛级数的性质,掌握幂级数的性质,会熟练展开函 数为幂级数,了解函数的幂级数展开的重要应用。 成绩考核形式为考试成绩考核形式:末考成绩(闭卷考试)(70%)+平时成绩(作业、 课堂提问、课堂讨论等)(30%)。成绩评定采用百分制,60 分为及格。 三、课程教学内容 第六章 微分中值定理及其应用 1.教学基本要求

让学生掌握微分中值定理及其应用:熟悉掌握利用罗必达法则的用法,熟练应用导数 判断函数相关性质。 2.要求学生掌握的基本概念、理论、方法 深刻理解拉格朗日定理及其推论,掌握定理的证明,它的几种形式。理解费尔马定理, 罗尔定理,柯西定理,泰勒定理的证明。能用拉格朗日定理及其推论证明某些不等式,掌握 利用函数的泰勒展开式求一些函数的极限的方法。熟悉掌握利用罗必达法则求各种不定型极 限的方法。掌握函数单调性与导数间的联系与几何意义:明确函数在某一点x。处单调的 含义。掌握极限的要领与它的局部性质。掌握函数凸凹的解析定义与几何意义。掌握函数单 调性,极值,凸凹性,拐点的判定方法。了解凸函数的基本性质。掌握利用导数证明不等式 的基本方法。掌握基本初等函数的特性作图方法。 3.教学重点和难点 教学重点是拉格朗日定理和函数的单调性:柯西中值定理和不定式极限:泰勒公式:函 数的极值与最大(小值:函数的凸性与拐点。教学难点是泰勒公式:函数作图。 4.教学内容 第一节拉格朗日定理和函数的单调性 1.罗尔定理与拉格朗日定理 2.单调函数 第二节 柯西中值定理和不定式极限 1.柯西中值定理 2.0/0型不定式极限 3./∞型不定式极限 4.其他类型不定式极限 第三节泰勒公式 1.泰勒定理 2.带皮亚诺型余项的泰勒公式 3.在近似计算中的应用 第四节 函数的极值与最大(小)值 1.极值判别法 2.最大值与最小值 第五节 函数的凸性与拐点 1.函数的凸性 2.拐点 第六节 函数图象的讨论
让学生掌握微分中值定理及其应用;熟悉掌握利用罗必达法则的用法,熟练应用导数 判断函数相关性质。 2.要求学生掌握的基本概念、理论、方法 深刻理解拉格朗日定理及其推论,掌握定理的证明,它的几种形式。理解费尔马定理, 罗尔定理,柯西定理,泰勒定理的证明。能用拉格朗日定理及其推论证明某些不等式,掌握 利用函数的泰勒展开式求一些函数的极限的方法。熟悉掌握利用罗必达法则求各种不定型极 限的方法。 掌握函数单调性与导数间的联系与几何意义;明确函数在某一点 x。处单调的 含义。掌握极限的要领与它的局部性质。掌握函数ÿĀ的解析定义与几何意义。掌握函数单 调性,极值,ÿĀ性,拐点的判定方法。了解ÿ函数的基本性质。掌握利用导数证明不等式 的基本方法。掌握基本初等函数的特性作图方法。 3.教学重点和难点 教学重点是拉格朗日定理和函数的单调性;柯西中值定理和不定式极限;泰勒公式;函 数的极值与最大(小)值;函数的ÿ性与拐点。教学难点是泰勒公式;函数作图。 4.教学内容 第一节 拉格朗日定理和函数的单调性 1. 罗尔定理与拉格朗日定理 2. 单调函数 第二节 柯西中值定理和不定式极限 1. 柯西中值定理 2. 0╱0 型不定式极限 3. ∞╱∞型不定式极限 4. 其他类型不定式极限 第三节 泰勒公式 1. 泰勒定理 2. 带皮亚诺型余项的泰勒公式 3. 在近似计算中的应用 第四节 函数的极值与最大(小)值 1. 极值判别法 2. 最大值与最小值 第五节 函数的凸性与拐点 1. 函数的ÿ性 2. 拐点 第六节 函数图象的讨论

1.函数作图步骤 第七章 实数的的完备性 1.教学基本要求 了解区间套定理,聚点定理,有限覆盖定理及实数完备性定理的等价关系。 2.要求学生掌握的基本概念、理论、方法 理解区间套定理,聚点定理,有限覆盖定理的意义。了解区间套定理,聚点定理,有限 覆盖定理。确界定理与单调有界定理,柯西收敛准则的等价性,理解实数完备性的基本含义。 理解“覆盖”,“区间套”,“聚点”的概念,弄清聚点与收敛子数列间的关系。 3.教学重点和难点 教学重点是区间套定理、聚点定理与有限覆盖定理。教学难点是有关实数完备性基本定 理的等价性的证明, 4.教学内容 第一节 实数完备性的基本定理 1.区间套定理与柯西收敛准则 2。聚点定理与有限覆盖定理 第八章 不定积分 1.教学基本要求 理解原函数和不定积分的概念,掌握不定积分的计算方法。 2.要求学生掌握的基本概念、理论、方法 深刻理解原函数和不定积分的概念,分清二者之间的区别与联系。理解不定积分的几何 意义。掌握不定积分的运算法则。牢固掌握换元积分法与分部积分法的技巧。掌握有理函数 积分法。掌握化简简单无理函数与三角函数为有理函数积分的方法。掌握特殊三角函数的积 分法。掌握查不定积分表的方法。理解初等函数的原函数不一定是初等函数,而有理函数的 原函数一定是初等函数。 3.教学重点和难点 教学重点是不定积分的概念、换元积分法、分部积分法,不定积分的基本公式,有理函 数积分的计算。教学难点是有理函数积分的计算 4.教学内容 第一节不定积分的概念和基本积分公式 1.原函数和不定积分的定义 2.不定积分的基本公式 第二节换元积分法和分部积分法
1. 函数作图步骤 第七章 实数的的完备性 1.教学基本要求 了解区间套定理,聚点定理,有限覆盖定理及实数完备性定理的等价关系。 2.要求学生掌握的基本概念、理论、方法 理解区间套定理,聚点定理,有限覆盖定理的意义。了解区间套定理,聚点定理,有限 覆盖定理。确界定理与单调有界定理,柯西收敛准则的等价性,理解实数完备性的基本含义。 理解“覆盖”,“区间套”,“聚点”的概念,弄清聚点与收敛子数列间的关系。 3.教学重点和难点 教学重点是区间套定理、聚点定理与有限覆盖定理。教学难点是有关实数完备性基本定 理的等价性的证明。 4.教学内容 第一节 实数完备性的基本定理 1. 区间套定理与柯西收敛准则 2. 聚点定理与有限覆盖定理 第八章 不定积分 1.教学基本要求 理解原函数和不定积分的概念,掌握不定积分的计算方法。 2.要求学生掌握的基本概念、理论、方法 深刻理解原函数和不定积分的概念,分清二者之间的区别与联系。理解不定积分的几何 意义。掌握不定积分的运算法则。牢固掌握换元积分法与分部积分法的技巧。掌握有理函数 积分法。掌握化简简单无理函数与三角函数为有理函数积分的方法。掌握特殊三角函数的积 分法。掌握查不定积分表的方法。理解初等函数的原函数不一定是初等函数,而有理函数的 原函数一定是初等函数. 3.教学重点和难点 教学重点是不定积分的概念、换元积分法、分部积分法,不定积分的基本公式,有理函 数积分的计算。教学难点是有理函数积分的计算。 4.教学内容 第一节 不定积分的概念和基本积分公式 1. 原函数和不定积分的定义 2. 不定积分的基本公式 第二节 换元积分法和分部积分法

1.换元积分法 2.分部积分法 第三节 有理函数和可化为有理函数的不定积分 1.有理函数的不定积分 2.三角函数有理式的不定积分 3.某些无理根式的不定积分 第九章 定积分 1.教学基本要求 理解定积分的概念和几何意义和可积条件,深刻理解微积分学基本定理,掌握定积分 的计算。 2.要求学生掌握的基本概念、理论、方法 深刻理解定积分定义及其几何意义。掌握可积的充分条件与必要条件。理解有界函数的 达布上和、下和的概念及其性质。理解有界函数上、下和的概念以及与定积分概念之间的关 系。掌握函数f(x)在[a,b]上可积的一些等价命题。深刻理解变上限积分的概念及其连续性, 可微性定理的证明。深刻理解微积分学基本定理,理解定积分与不定积分,微积分与积分之 间的内在联系。熟练掌握用牛顿一一莱布尼兹公式,变量替换公式及分步积分公式计算定积 分。掌握证明函数可积性的方法。 3.教学重点和难点 教学重点是定积分的概念,可积条件,微积分基本定理,定积分的计算。教学难点是 可积条件,微积分基本定理 4.教学内容 第一节定积分的概念 1.问题提出 2.定积分的定义 第二节 牛顿一莱布尼茨公式 1.牛顿-莱布尼茨公式证明及应用 第三节可积条件 1,可积的必要条件 2.可积的充要条件 3.可积函数类 第四节 定积分的性质 1.定积分的基本性质
1. 换元积分法 2. 分部积分法 第三节 有理函数和可化为有理函数的不定积分 1. 有理函数的不定积分 2. 三角函数有理式的不定积分 3. 某些无理根式的不定积分 第九章 定积分 1.教学基本要求 理解定积分的概念和几何意义和可积条件,深刻理解微积分学基本定理,掌握定积分 的计算。 2.要求学生掌握的基本概念、理论、方法 深刻理解定积分定义及其几何意义。掌握可积的充分条件与必要条件。理解有界函数的 达布上和、下和的概念及其性质。理解有界函数上、下和的概念以及与定积分概念之间的关 系。掌握函数 f(x)在[a,b]上可积的一些等价命题。深刻理解变上限积分的概念及其连续性, 可微性定理的证明。深刻理解微积分学基本定理,理解定积分与不定积分,微积分与积分之 间的内在联系。熟练掌握用牛顿——莱布尼兹公式,变量替换公式及分步积分公式计算定积 分。掌握证明函数可积性的方法。 3.教学重点和难点 教学重点是定积分的概念 ,可积条件,微积分基本定理,定积分的计算。教学难点是 可积条件,微积分基本定理。 4.教学内容 第一节 定积分的概念 1. 问题提出 2. 定积分的定义 第二节 牛顿-莱布尼茨公式 1. 牛顿-莱布尼茨公式证明及应用 第三节 可积条件 1. 可积的必要条件 2. 可积的充要条件 3. 可积函数类 第四节 定积分的性质 1. 定积分的基本性质

2.积分中值定理 第五节 微积分基本定理·定积分的计算(续) 1.变限积分与原函数存在定理 2.换元积分法和分部积分法 3.泰勒公式的积分型余项 第十章 定积分的应用 1.教学基本要求 掌握应用定积分求面积、体积、弧长和旋转曲面面积的公式和方法及定积分在物理上 的应用。 2.要求学生掌握的基本概念、理论、方法 理解曲线段可求长的慨念。掌握光滑曲线、微分曲线的曲率,曲率半径,曲率圆等概念。 掌握旋转曲面面积的公式。掌握弧长公式的推导。掌握平面图形面积的求法和已知截面面积 函数求体积的公式 3.教学重点和难点 教学重点定积分在几何和物理方面的应用。教学难点是旋转曲面面积公式,微元法。 4.教学内容 第一节 平面图形的面积 1.求直角坐标系平面图形的面积 2.参量方程下平面图形的面积 3.极坐标下平面图形的面积 第二节 由平行截面面积求体积 1.几何体的体积 2.旋转体的体积 第三节 平面曲线的弧长与曲率 1.平面曲线的弧长 2.曲率 第四节 旋转曲面的面积 1.微元法 2.旋转曲面的面积 第五节 定积分在物理上的应用 1.液体的静压力 2.引力 3.功与平均功率
2. 积分中值定理 第五节 微积分基本定理·定积分的计算(续) 1. 变限积分与原函数存在定理 2. 换元积分法和分部积分法 3. 泰勒公式的积分型余项 第十章 定积分的应用 1.教学基本要求 掌握应用定积分求面积、体积、弧长和旋转曲面面积的公式和方法及定积分在物理上 的应用。 2.要求学生掌握的基本概念、理论、方法 理解曲线段可求长的慨念。掌握光滑曲线、微分曲线的曲率,曲率半径,曲率圆等概念。 掌握旋转曲面面积的公式。掌握弧长公式的推导。掌握平面图形面积的求法和已知截面面积 函数求体积的公式。 3.教学重点和难点 教学重点定积分在几何和物理方面的应用。教学难点是旋转曲面面积公式,微元法。 4.教学内容 第一节 平面图形的面积 1. 求直角坐标系平面图形的面积 2. 参量方程下平面图形的面积 3. 极坐标下平面图形的面积 第二节 由平行截面面积求体积 1. 几何体的体积 2. 旋转体的体积 第三节 平面曲线的弧长与曲率 1. 平面曲线的弧长 2. 曲率 第四节 旋转曲面的面积 1. 微元法 2. 旋转曲面的面积 第五节 定积分在物理上的应用 1. 液体的静压力 2. 引力 3. 功与平均功率

第十一章反常积分 1.教学基本要求 理解无穷限反常积分、无界函数反常积分概念。熟练掌握反常积分的收敛判别法与 反常积分的计算方法.。 2.要求学生掌握的基本概念、理论、方法 理解无穷限非正常积分和瑕积分敛散性概念,掌握非正常积分的计算,绝对收敛和条件 收敛的概念,非正常积分的Cauchy收敛原理,非负函数非正常积分的比较判别法,Cauchy 判别法,以及一般函数非正常积分的Abel,Dirichlet判别法。 3.教学重点和难点 教学重点反常积分概念和收敛性的判断。教学难点是收敛性的判断 4.教学内容 第一节反常积分的概念 1.问题提出 2.两类反常积分的定义 第二节 无穷积分的性质和收敛判断 1.无穷积分的性质 2.比较判别法 3.Abel,Dirichlet判别法 第三节 瑕积分的性质与收敛判断 1.瑕积分的性质 2.比较判别法 3.Abel,Dirichlet判别法 第十二章数项级数 1.教学基本要求 理解级数收敛与发散的概念,掌握正项级数和一般项级数收敛的判别。熟练判断绝对 收敛和条件收敛。 2.要求学生掌握的基本概念、理论、方法 掌握数项级数收敛与发散的概念,理解级数的意义。正确区分绝对收敛,条件收敛,收 敛这三个定义的不同内涵,掌握绝对收敛级数与条件收敛级数在运算性质上的差异。掌握收 敛级数的基本性质及其证明。掌握柯西准则,正项级数的收敛原则,比较原则,比值判别法 与根值判别法以及交错级数的莱布尼兹判别法的内容及证明。能熟悉运用数项级数的收敛准 则,比较判别法,比值判别法,根式判别法,积分判别法判定正项数的敛散性。熟练运用莱
第十一章 反常积分 1.教学基本要求 理解无穷限反常积分、无界函数反常积分概念。 熟练掌握反常积分的收敛判别法与 反常积分的计算方法.。 2.要求学生掌握的基本概念、理论、方法 理解无穷限非正常积分和瑕积分敛散性概念,掌握非正常积分的计算,绝对收敛和条件 收敛的概念,非正常积分的 Cauchy 收敛原理,非负函数非正常积分的比较判别法,Cauchy 判别法,以及一般函数非正常积分的 Abel,Dirichlet 判别法。 3.教学重点和难点 教学重点反常积分概念和收敛性的判断。教学难点是收敛性的判断。 4.教学内容 第一节 反常积分的概念 1. 问题提出 2. 两类反常积分的定义 第二节 无穷积分的性质和收敛判断 1. 无穷积分的性质 2. 比较判别法 3. Abel,Dirichlet 判别法 第三节 瑕积分的性质与收敛判断 1. 瑕积分的性质 2. 比较判别法 3. Abel,Dirichlet 判别法 第十二章 数项级数 1.教学基本要求 理解级数收敛与发散的概念,掌握正项级数和一般项级数收敛的判别。熟练判断绝对 收敛和条件收敛。 2.要求学生掌握的基本概念、理论、方法 掌握数项级数收敛与发散的概念,理解级数的意义。正确区分绝对收敛,条件收敛,收 敛这三个定义的不同内涵,掌握绝对收敛级数与条件收敛级数在运算性质上的差异。掌握收 敛级数的基本性质及其证明。掌握柯西准则,正项级数的收敛原则,比较原则,比值判别法 与根值判别法以及交错级数的莱布尼兹判别法的内容及证明。能熟悉运用数项级数的收敛准 则,比较判别法,比值判别法,根式判别法,积分判别法判定正项数的敛散性。熟练运用莱

布尼兹判别法判定交错级数的敛散性,并能正确估计余项。掌握利用阿贝尔判别法和狄利克 雷判别法任意项数的敛散性的技巧。具有构造简单反例的能力. 3.教学重点和难点 教学重点数项级数及敛散性概念,级数的基本性质,正项级数的判别法,任意项级数的 判别法。教学难点是正项级数的判别法,任意项级数的判别法。 4.教学内容 第一节级数的收敛性 1.数项级数敛散性概念 2.级数收敛的必要条件和其它性质 3.一些级数求和 第二节正项级数 1.正项级数收敛性的一般判别原则 2.比式判别法和根式判别法 3.积分判别法 第三节 一般项级数 1.交错级数 2.绝对收敛及其性质 3.Abel,Dirichlet判别法 第十三章 函数列和函数项级数 1.教学基本要求 理解函数列和函数项级数的概念,掌握函数列和函数项级数收敛和一致收敛的判断 学握函数列和函数项级数的性质。 2.要求学生掌握的基本概念、理论、方法 理解收敛域,函数列的极限函数与函数项级数的和函数的意义:掌握函数列与函数项级 数的相互转化关系。深刻理解函数列与函数项级数的一致收敛概念的含义,几何解释及逻 辑非命题。正确区分在一个域上点点收敛与一致收敛的差异,了解他们之间的联系。掌握函 数列极限函数与函数项级数和函数的分析性质及其证明。能掌握应用维尔斯特拉斯判别法判 定函数项级数的一致收敛性,堂握使用阿贝尔判别法和狄利克雷判别法判定函数项级数一致 收敛性的方法 3.教学重点和难点 教学重点函数列和函数项级数一致收敛的概念和其判别方法,一致收敛函数项级数和函 数列的连续、可导和可积性。教学难点是函数列和函数项一致收敛 4.教学内容
布尼兹判别法判定交错级数的敛散性,并能正确估计余项。掌握利用阿贝尔判别法和狄利克 雷判别法任意项数的敛散性的技巧。具有构造简单反例的能力. 3.教学重点和难点 教学重点数项级数及敛散性概念,级数的基本性质,正项级数的判别法,任意项级数的 判别法。教学难点是正项级数的判别法,任意项级数的判别法。 4.教学内容 第一节 级数的收敛性 1. 数项级数敛散性概念 2. 级数收敛的必要条件和其它性质 3. 一些级数求和 第二节 正项级数 1. 正项级数收敛性的一般判别原则 2. 比式判别法和根式判别法 3. 积分判别法 第三节 一般项级数 1. 交错级数 2. 绝对收敛及其性质 3. Abel,Dirichlet 判别法 第十三章 函数列和函数项级数 1.教学基本要求 理解函数列和函数项级数的概念,掌握函数列和函数项级数收敛和一致收敛的判断。 掌握函数列和函数项级数的性质。 2.要求学生掌握的基本概念、理论、方法 理解收敛域,函数列的极限函数与函数项级数的和函数的意义;掌握函数列与函数项级 数 的相互转化关系。深刻理解函数列与函数项级数的一致收敛概念的含义,几何解释及逻 辑非命题。正确区分在一个域上点点收敛与一致收敛的差异,了解他们之间的联系。掌握函 数列极限函数与函数项级数和函数的分析性质及其证明。能掌握应用维尔斯特拉斯判别法判 定函数项级数的一致收敛性。掌握使用阿贝尔判别法和狄利克雷判别法判定函数项级数一致 收敛性的方法. 3.教学重点和难点 教学重点函数列和函数项级数一致收敛的概念和其判别方法,一致收敛函数项级数和函 数列的连续、可导和可积性。教学难点是函数列和函数项一致收敛。 4.教学内容

第一节 一致收敛性 1.函数列及其一致收敛性 2。函数项级数及其一致收敛性 3.函数项级数的一致收敛性判别法 第二节 一致收敛函数列与函数项级数的性质 1.一致收敛函数列的性质 2.一致收敛函数项级数的性质 第十四章 幂级数 1.教学基本要求 掌握幂级数的收敛半径收敛域的判断,幂级数的性质和运算,掌握函数展开成幂级数 的方法。 2.要求学生掌握的基本概念、理论、方法 理解幂级数的收敛半径,收敛区间和收敛域的概念。掌握函数的泰勒级数的概念与展开 式。掌握阿贝尔定理及其证明。熟练学握求幂级数收敛半径,收敛区间和收敛域的方法。能 熟练利用已知展开式求出数的幂级数,掌握幂级数的运算。掌握幂级数的和函数的分析性质。 能利用幂级数展开式进行近似计算。 3.教学重点和难点 教学重点幂级数概念、幂级数的敛散性及其判定,幂级数的性质,幂级数的运算。Tyo「 级数、初等函数的幂级数展开,应用幂级数的展开式做近似计算。教学难点是初等函数的幂 级数展开应用幂级数的性质求和函数的方法。 4.教学内容 第一节幂级数 1.幂级数的收敛区间 2.幂级数的性质 3.幂级数的运算 第二节 函数的幂级数展开 1.泰勒级数 2.初等函数的幂级数展开 四、学时分配 1,讲授内容及学时分配 章序 内容 课时 备注 六 微分中值定理及其应用 18
第一节 一致收敛性 1. 函数列及其一致收敛性 2. 函数项级数及其一致收敛性 3. 函数项级数的一致收敛性判别法 第二节 一致收敛函数列与函数项级数的性质 1. 一致收敛函数列的性质 2. 一致收敛函数项级数的性质 第十四章 幂级数 1.教学基本要求 掌握幂级数的收敛半径收敛域的判断,幂级数的性质和运算,掌握函数展开成幂级数 的方法。 2.要求学生掌握的基本概念、理论、方法 理解幂级数的收敛半径,收敛区间和收敛域的概念。掌握函数的泰勒级数的概念与展开 式。掌握阿贝尔定理及其证明。熟练掌握求幂级数收敛半径,收敛区间和收敛域的方法。能 熟练利用已知展开式求出数的幂级数,掌握幂级数的运算。掌握幂级数的和函数的分析性质。 能利用幂级数展开式进行近似计算。 3.教学重点和难点 教学重点幂级数概念、幂级数的敛散性及其判定,幂级数的性质,幂级数的运算。Taylor 级数、初等函数的幂级数展开,应用幂级数的展开式做近似计算。教学难点是初等函数的幂 级数展开应用幂级数的性质求和函数的方法。 4.教学内容 第一节 幂级数 1. 幂级数的收敛区间 2. 幂级数的性质 3. 幂级数的运算 第二节 函数的幂级数展开 1. 泰勒级数 2. 初等函数的幂级数展开 四、学时分配 1.讲授内容及学时分配 章序 内容 课时 备注 六 微分中值定理及其应用 18
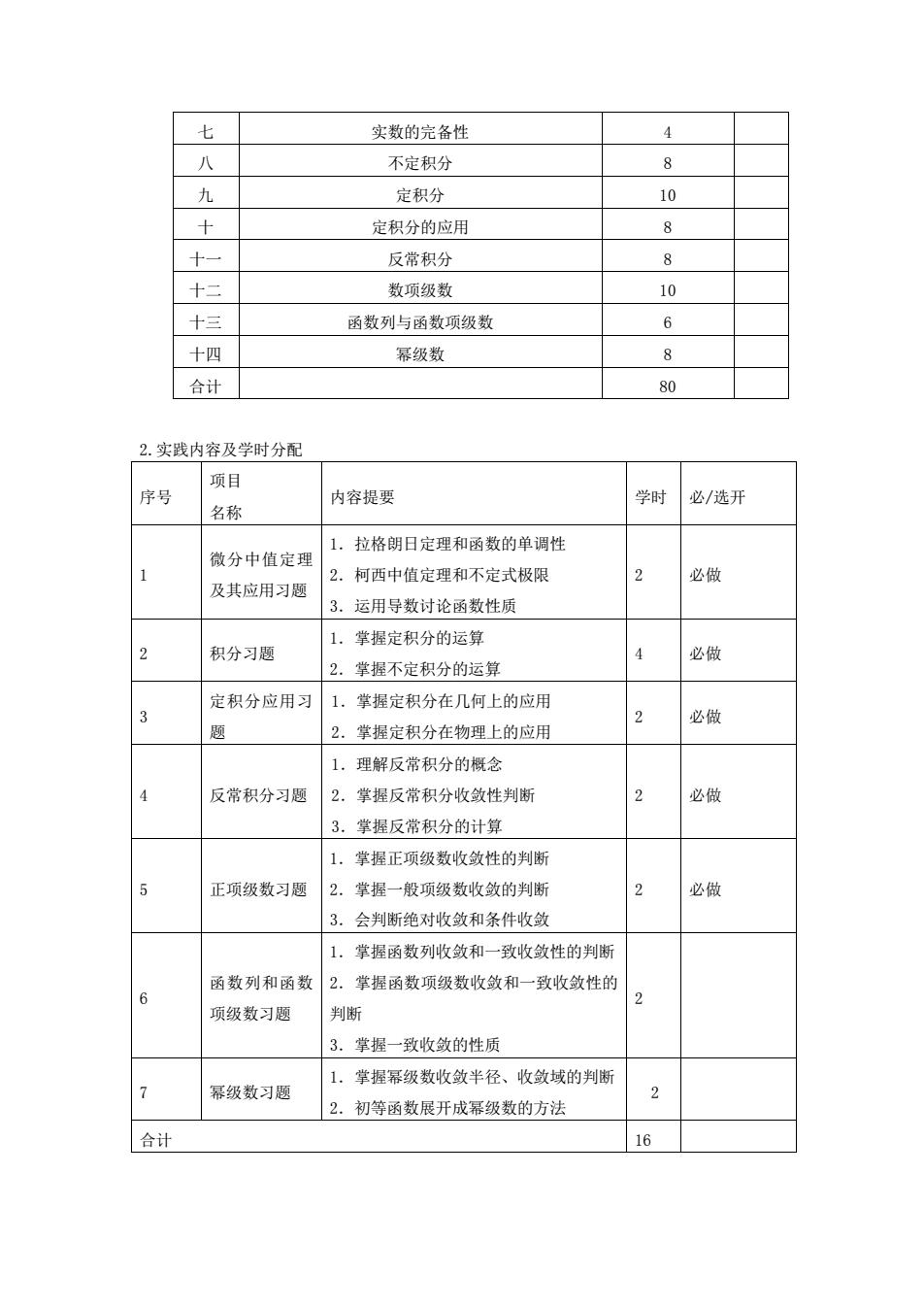
七 实数的完备性 4 不定积分 九 定积分 10 定积分的应用 8 十一 反常积分 8 十二 数项级数 10 十三 函数列与函数项级数 6 十四 幂级数 8 合计 80 2.实践内容及学时分面 序号 项目 内容提要 必/选开 名称 学时 1,拉格朗日定理和函数的单调性 微分中值定理 2.柯西中值定理和不定式极限 必做 及其应用习题 3.运用导数讨论函数性质 1. 掌握定积分的运算 2 积分习题 必做 2.掌握不定积分的运算 定积分应用习 1,掌握定积分在几何上的应用 3 2 必做 题 2.堂握定积分在物理上的应用 1.理解反常积分的概念 4 反常积分习题 2 掌握反常积分收敛性判断 2 必做 3.掌握反常积分的计算 L,掌握正项级数收敛性的判 5 正项级数习题 2.掌握一般项级数收敛的判 必做 3.会判断绝对收敛和条件收敛 1.掌握函数列收敛和一致收敛性的判断 函数列和函数 2.掌握函数项级数收敛和一致收敛性的 6 2 项级数习题 判新 3.掌握一致收敛的性质 1.掌握幂级数收敛半径、收敛域的判断 幂级数习题 2.初等函数展开成幂级数的方法 合计 16
七 实数的完备性 4 八 不定积分 8 九 定积分 10 十 定积分的应用 8 十一 反常积分 8 十二 数项级数 10 十三 函数列与函数项级数 6 十四 幂级数 8 合计 80 2.实践内容及学时分配 序号 项目 名称 内容提要 学时 必/选开 1 微分中值定理 及其应用习题 1.拉格朗日定理和函数的单调性 2.柯西中值定理和不定式极限 3.运用导数讨论函数性质 2 必做 2 积分习题 1.掌握定积分的运算 2.掌握不定积分的运算 4 必做 3 定积分应用习 题 1.掌握定积分在几何上的应用 2.掌握定积分在物理上的应用 2 必做 4 反常积分习题 1.理解反常积分的概念 2.掌握反常积分收敛性判断 3.掌握反常积分的计算 2 必做 5 正项级数习题 1.掌握正项级数收敛性的判断 2.掌握一般项级数收敛的判断 3.会判断绝对收敛和条件收敛 2 必做 6 函数列和函数 项级数习题 1.掌握函数列收敛和一致收敛性的判断 2.掌握函数项级数收敛和一致收敛性的 判断 3.掌握一致收敛的性质 2 7 幂级数习题 1.掌握幂级数收敛半径、收敛域的判断 2.初等函数展开成幂级数的方法 2 合计 16

五、主用教材及参考书 (一)主用教材: 《数学分析》(上、下册)(第四版)主编:华东师范大学数学系出版社:高等教有 出版社出版时间:2010年。 (二)参考书: 1.《数学分析》(上、下册)(第三版)主编:复旦大学数学系出版社:高等教育出 版社出版时间:1992年。 2。《数学分析》(上、下册)(第三版)主编:刘玉琏,傅沛仁出版社:高等教有出 版社出版时间:1991年。 3.《数学分析习题课课程》(上、下册)主编:郑英元,毛羽辉,宋国栋等出版社: 高等教有出版社出版时间:1994年。 4.《数学分析习题集》主编:吉米多维奇出版社:高等教有出版社出版时间 1982年。 执笔:韦毅华 审定:张泰梁桂珍
五、主用教材及参考书 (一)主用教材: 《数学分析》(上、下册)(第四版) 主编:华东师范大学数学系 出版社:高等教育 出版社 出版时间:2010 年。 (二)参考书: 1. 《数学分析》(上、下册)(第三版)主编:复旦大学数学系 出版社:高等教育出 版社 出版时间:1992 年。 2. 《数学分析》(上、下册)(第三版)主编:刘玉琏,傅沛仁 出版社:高等教育出 版社 出版时间:1991 年。 3. 《数学分析习题课课程》(上、下册) 主编:郑英元,毛羽辉,宋国栋等 出版社: 高等教育出版社 出版时间:1994 年。 4. 《数学分析习题集》 主编:吉米多维奇 出版社:高等教育出版社 出版时间: 1982 年。 执笔:韦毅华 审定:张秦 梁桂珍