
Unsupervised Learning: Neighbor Embedding
Unsupervised Learning: Neighbor Embedding
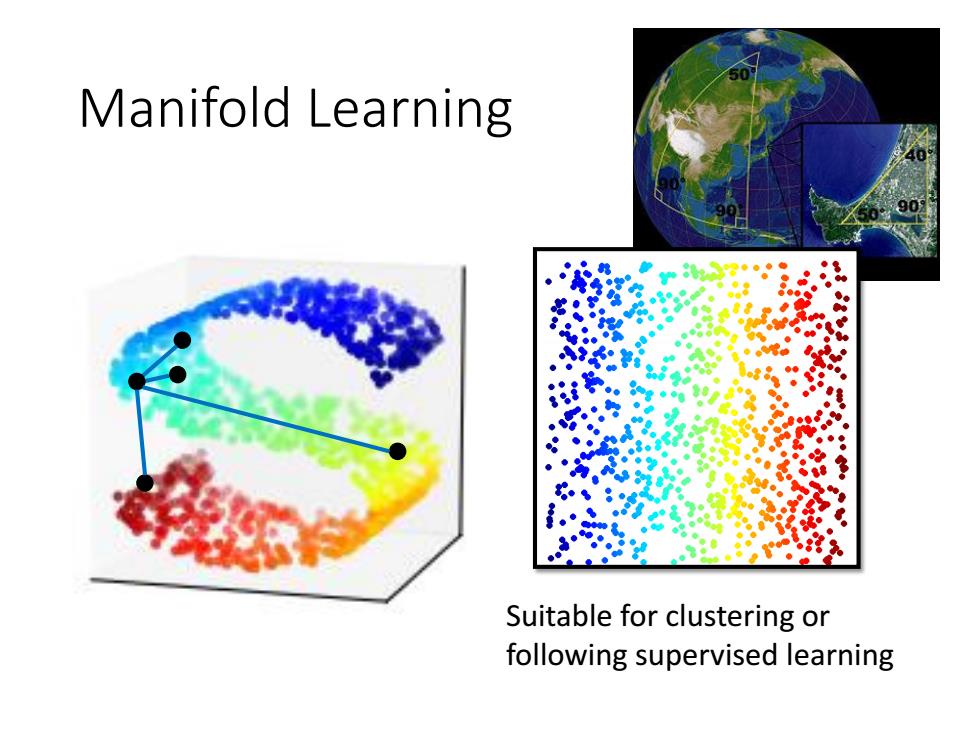
Manifold Learning Suitable for clustering or following supervised learning
Manifold Learning Suitable for clustering or following supervised learning
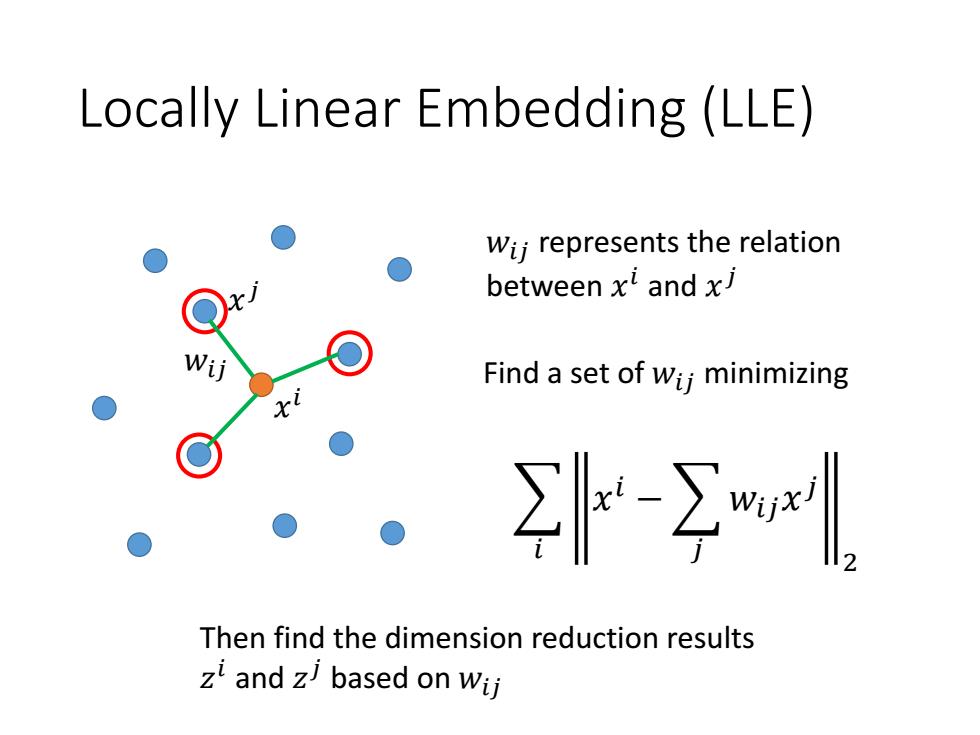
Locally Linear Embedding (LLE) Wij represents the relation between xl and x Find a set of wii minimizing k-yl Then find the dimension reduction results zi and z based on wij
Locally Linear Embedding (LLE) 𝑥 𝑖 𝑥 𝑗 𝑤𝑖𝑗 𝑤𝑖𝑗 represents the relation between 𝑥 𝑖 and 𝑥 𝑗 Find a set of 𝑤𝑖𝑗 minimizing 𝑖 𝑥 𝑖 − 𝑗 𝑤𝑖𝑗𝑥 𝑗 2 Then find the dimension reduction results 𝑧 𝑖 and 𝑧 𝑗 based on 𝑤𝑖𝑗
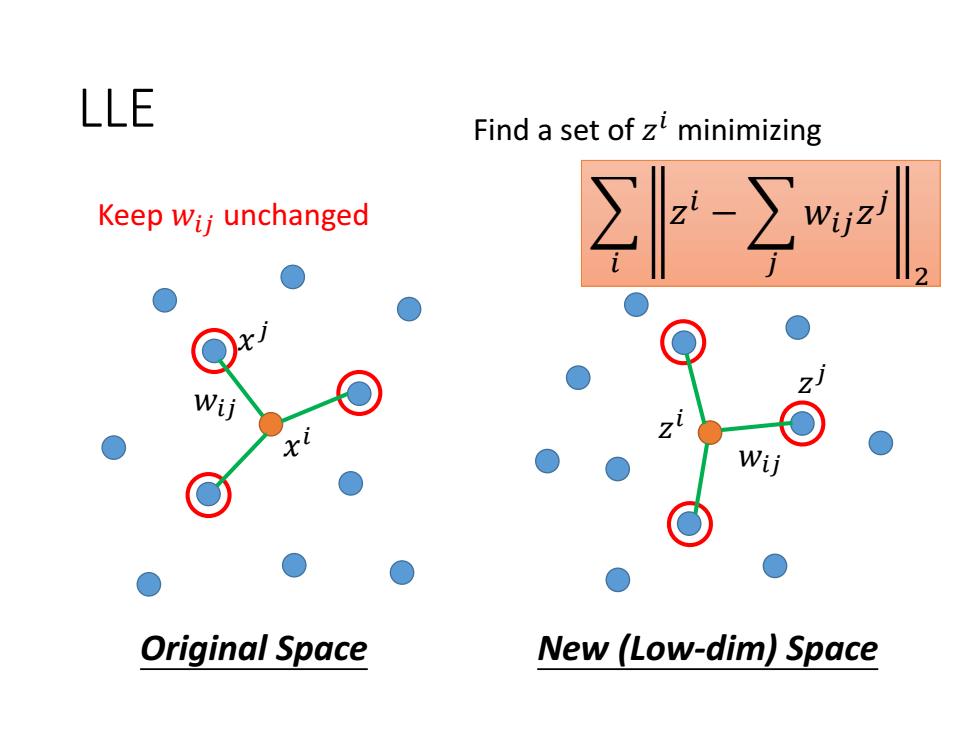
LLE Find a set of z minimizing Keep wij unchanged -Σ Wi Original Space New (Low-dim)Space
LLE 𝑥 𝑖 𝑥 𝑗 𝑤𝑖𝑗 𝑤𝑖𝑗 𝑧 𝑗 𝑧 𝑖 Original Space New (Low-dim) Space Find a set of 𝑧 𝑖 minimizing Keep 𝑤𝑖𝑗 unchanged 𝑖 𝑧 𝑖 − 𝑗 𝑤𝑖𝑗𝑧 𝑗 2

LLE xt,xi Wij 在地領為連理校 在天顧作出墨焉 Wij Source of image: http://feetsprint.blogspot.tw/2016 /02/blog-post_29.html
LLE Source of image: http://feetsprint.blogspot.tw/2016 /02/blog-post_29.html 𝑧 𝑖 ,𝑧 𝑗 𝑤𝑖𝑗 𝑤𝑖𝑗 𝑥 𝑖 ,𝑥 𝑗

LLE Lawrence K.Saul,Sam T.Roweis,"Think Globally,Fit Locally: Unsupervised Learning of Low Dimensional Manifolds",JMLR,2013 K=5 K=6 K= K=10 12 16 18 K=20 K=30 K=40 K=60
LLE Lawrence K. Saul, Sam T. Roweis, “Think Globally, Fit Locally: Unsupervised Learning of Low Dimensional Manifolds”, JMLR, 2013

Laplacian Eigenmaps Graph-based approach Distance defined by graph approximate the distance on manifold Construct the data points as a graph
Laplacian Eigenmaps • Graph-based approach Construct the data points as a graph Distance defined by graph approximate the distance on manifold

similarity Laplacian Eigenmaps Wi,j= If connected 0 otherwise Review in semi-supervised learning:If x1 and x2 are close in a high density region,1 and 2 are probably the same. t=∑co )+ As a regularization term s=2∑0-'=yy L:(R+U)x(R+U)matrix S evaluates how smooth your label is Graph Laplacian L=D-W
Laplacian Eigenmaps • Review in semi-supervised learning: If 𝑥 1 and 𝑥 2 are close in a high density region, 𝑦 ො 1 and 𝑦 ො 2 are probably the same. 𝐿 = 𝑥 𝑟 𝐶 𝑦 𝑟 , 𝑦 ො 𝑟 +𝜆𝑆 As a regularization term = 𝒚 𝑇 𝑆 = 𝐿𝒚 1 2 𝑖,𝑗 𝑤𝑖,𝑗 𝑦 𝑖 − 𝑦 𝑗 2 L: (R+U) x (R+U) matrix Graph Laplacian 𝐿 = 𝐷 − 𝑊 S evaluates how smooth your label is 𝑤𝑖,𝑗 = 0 similarity If connected otherwise

Laplacian Eigenmaps Dimension Reduction:If x1 and x2 are close in a high density region,z1 and z2 are close to each other. s=∑ue-z Any problem?How about zi=z=0? Giving some constraints to z: If the dim of z is M,Span(z1,z2,...N)=RM Spectral clustering:clustering on z Belkin,M.,Niyogi,P.Laplacian eigenmaps and spectral techniques for embedding and clustering.Advances in neural information processing systems.2002
Laplacian Eigenmaps • Dimension Reduction: If 𝑥 1 and 𝑥 2 are close in a high density region, 𝑧 1 and 𝑧 2 are close to each other. 𝑆 = 1 2 𝑖,𝑗 𝑤𝑖,𝑗 𝑧 𝑖 − 𝑧 𝑗 2 Spectral clustering: clustering on z Any problem? How about 𝑧 𝑖 = 𝑧 𝑗 = 𝟎? Giving some constraints to z: If the dim of z is M, Span{z1 , z2 , … z N} = RM Belkin, M., Niyogi, P. Laplacian eigenmaps and spectral techniques for embedding and clustering. Advances in neural information processing systems . 2002

T-distributed Stochastic Neighbor Embedding (t-SNE) Problem of the previous approaches Similar data are close,but different data may collapse LLE on MNIST LLE on COIL-20
T-distributed Stochastic Neighbor Embedding (t-SNE) • Problem of the previous approaches • Similar data are close, but different data may collapse LLE on MNIST LLE on COIL-20