
分类问题2 1
分类问题2 1

Outline ·4.3补充:优化算法NNDL《神经网络与深度学习 》附录p418-425 ·4.3支持向量机 哈尔滨工业大学计算机学院刘远超 2
Outline • 4.3 补充:优化算法NNDL《神经⽹络与深度学习 》附录p418-425 • 4.3 ⽀持向量机 哈尔滨工业大学计算机学院 刘远超 2

数学优化的类型 ·离散优化(Discrete Optimization) ·组合优化(Combinatorial Optimization) ·整数规划(Integer Programming) ·连续优化(Continuous Optimization) ·无约束优化(Unconstrained Optimization) ·约束优化(Constrained Optimization) ·线性规划(Linear Programming) ·非线性规划(Nonlinear Programming) ·凸优化(Convex Optimization) 哈尔滨工业大学计算机学院刘远超 3
数学优化的类型 • 离散优化(Discrete Optimization) • 组合优化(Combinatorial Optimization) • 整数规划(Integer Programming) • 连续优化 (Continuous Optimization) • ⽆约束优化(Unconstrained Optimization) • 约束优化(Constrained Optimization) • 线性规划(Linear Programming) • ⾮线性规划(Nonlinear Programming) • 凸优化(Convex Optimization) 哈尔滨工业大学计算机学院 刘远超 3
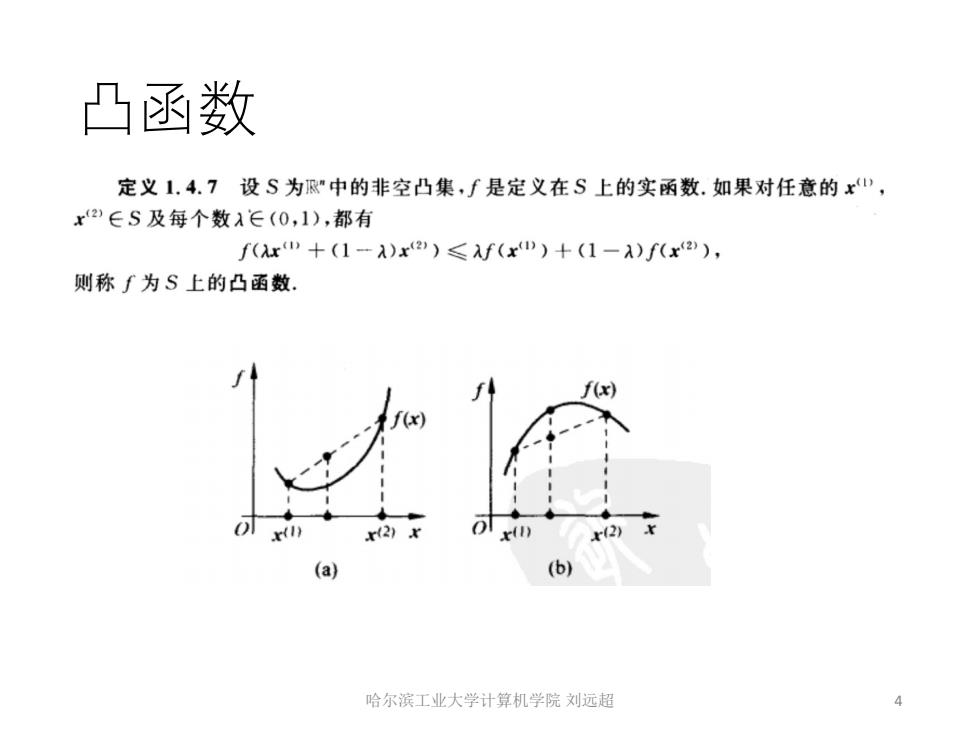
凸函数 定义1.4.7设S为"中的非空凸集,f是定义在S上的实函数.如果对任意的x”, x2∈S及每个数1∈(0,1),都有 f(x+(1-A)x2)≤f(x)+(1-A)f(x2), 则称f为S上的凸函数 f(x) (x) x(2)x ol xin r2) (a) (b) 哈尔滨工业大学计算机学院刘远超 4
凸函数 哈尔滨工业大学计算机学院 刘远超 4
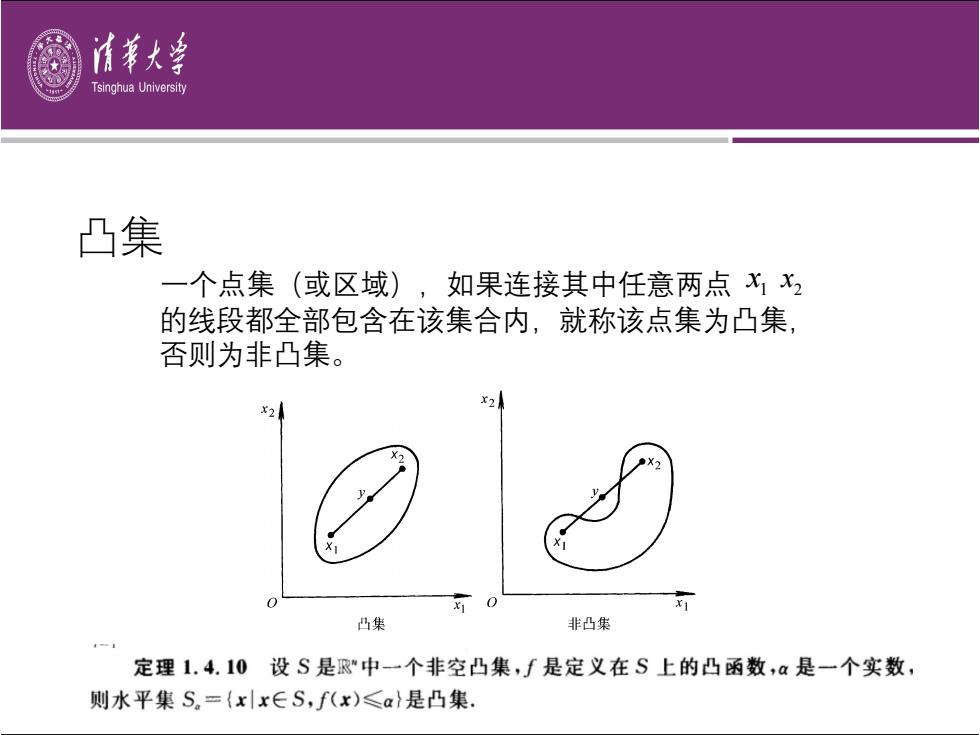
清蒂大学 Tsinghua University 凸集 一个点集(或区域),如果连接其中任意两点xx2 的线段都全部包含在该集合内,就称该点集为凸集, 否则为非凸集。 X2 凸集 非凸集 定理1.4.10设S是歌"中一个非空凸集,f是定义在S上的凸函数,a是一个实数, 则水平集S。={xx∈S,f(x)≤a}是凸集
的线段都全部包含在该集合内,就称该点集为凸集, 否则为⾮凸集。 ⼀个点集(或区域),如果连接其中任意两点 1 x 2 x 凸集

门第大兰 Tsinghua University 凸性条件 1.根据一阶导数(函数的梯度)来判断函数的凸性 设f(x)为定义在凸集R上,且具有连续的一阶导数 的函数,则(x)在R上为凸函数的充要条件是对凸 集R内任意不同两点x,x2,不等式 f(x)f(x)+(xx)'vf(x) 恒成立
1.根据⼀阶导数(函数的梯度)来判断函数的凸性 设f(x)为定义在凸集R上,且具有连续的⼀阶导数 的函数,则f(x)在R上为凸函数的充要条件是对凸 集R内任意不同两点 x1 x2,不等式 ( 2 1 21 1 ) ( ) ( ) ( ) T fx fx x x fx ³ + - Ñ 恒成⽴。 凸性条件

清蒋大兰 Tsinghua University 凸性条件 2.根据二阶导数(Hesse矩阵)来判断函数的凸性 设fx)为定义在凸集R上且具有连续二阶导数的 函数,则f(x)在R上为凸函数的充要条件: Hesse?矩阵在R上处处半正定 f在x处的Hesse矩阵为nXn矩阵V2f(x),第i行第j列元素为 [fx1,=铝 2f2,1≤ij≤m
2.根据⼆阶导数( Hesse矩阵)来判断函数的凸性 设f(x)为定义在凸集R上且具有连续⼆阶导数的 函数,则f(x)在R上为凸函数的充要条件: Hesse矩阵在R上处处半正定 凸性条件

清蒂大当 Tsinghua University 凸优化 对于约束优化问题 minf(x) s.t. 8,(x)≤0j=1,2,,m 若f(x)g,(x)都为凸函数,则此问题为凸规划。 凸优化问题是一种特殊的约束优化问题,需满足目标函 数为凸函数,并且等式约束函数为线性函数,不等式 约束函数为凸函数(小于等于0,可行域为凸集)
对于约束优化问题 min f x( ) s t. . ( ) 0 j g x £ j m =1, 2,..., 若 f x( ) g x j ( )都为凸函数,则此问题为凸规划。 凸优化 凸优化问题是一种特殊的约束优化问题,需满足目标函 数为凸函数,并且等 式约束函数为线性函数,不等式 约束函数为凸函数(小于等于0,可行域为凸集)

清蒋大兰 Tsinghua University 凸优化的性质 1若给定-点,则集合R={f)}为凸集。 2.可行域R={850l2m}为凸集 3凸规划的任何局部最优解就是全局最优解
1.若给定⼀点 , 则集合 0 x 为凸集。 2.可⾏域 为凸集 3.凸规划的任何局部最优解就是全局最优解 凸优化的性质

消荐大多 Tsinghua University 凸优化问题 ·凸优化问题:指约束最优化问题 min :f(w网 s.t. g,(w≤0,i=1,2,…,k h(w)=0,i=1,2,…,1 ·其中,目标函数f(w)和约束函数g(w都是Rn上连续可微的凸函数, 约束函数h(w)是Rn上的仿射函数 ·当目标函数为二次函数,g函数为仿射函数时,为凸二次规划问 题
• 凸优化问题: 指约束最优化问题 • 其中,⽬标函数f(w) 和约束函数gi (w)都是Rn上连续可微的凸函数, 约束函数hj (w)是Rn上的仿射函数 • 当⽬标函数为⼆次函数,g函数为仿射函数时,为凸⼆次规划问 题。 凸优化问题