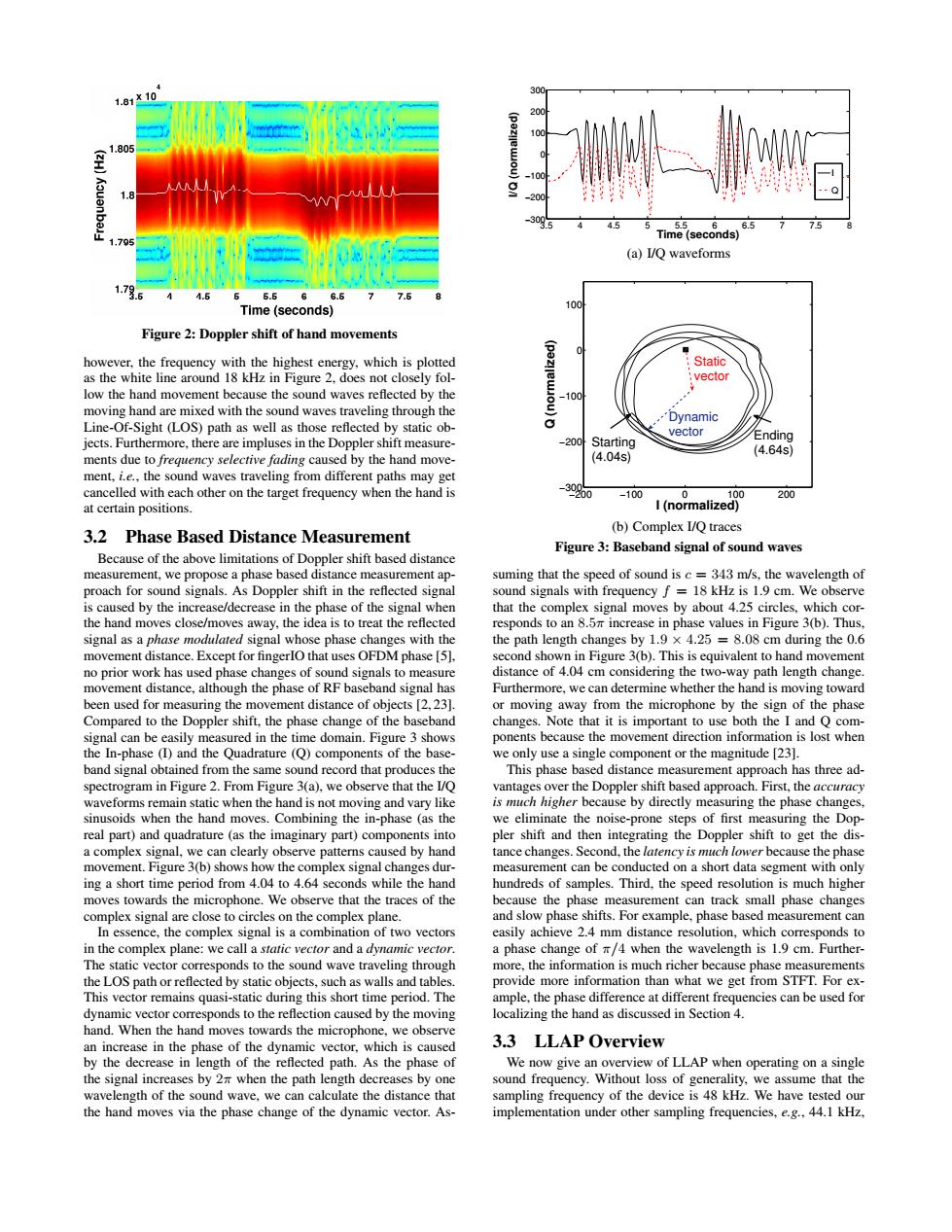
1.81X10 g 6.5 79 Time(seconds) 170 (a)I/Q waveforms 5.5 6 6.5 7.5 Time(seconds) 100 Figure 2:Doppler shift of hand movements however,the frequency with the highest energy,which is plotted Static as the white line around 18 kHz in Figure 2,does not closely fol- vector low the hand movement because the sound waves reflected by the -100 moving hand are mixed with the sound waves traveling through the 'Dynamic Line-Of-Sight (LOS)path as well as those reflected by static ob- vector jects.Furthermore,there are impluses in the Doppler shift measure- -200 Starting Ending (4.04s) (4.64s) ments due to frequency selective fading caused by the hand move- ment,i.e.,the sound waves traveling from different paths may get cancelled with each other on the target frequency when the hand is 30000 -100 100 200 at certain positions. I(normalized) (b)Complex I/Q traces 3.2 Phase Based Distance Measurement Figure 3:Baseband signal of sound waves Because of the above limitations of Doppler shift based distance measurement,we propose a phase based distance measurement ap- suming that the speed of sound is c=343 m/s,the wavelength of proach for sound signals.As Doppler shift in the reflected signal sound signals with frequency f 18 kHz is 1.9 cm.We observe is caused by the increase/decrease in the phase of the signal when that the complex signal moves by about 4.25 circles,which cor- the hand moves close/moves away,the idea is to treat the reflected responds to an 8.5 increase in phase values in Figure 3(b).Thus signal as a phase modulated signal whose phase changes with the the path length changes by 1.9 x 4.25 =8.08 cm during the 0.6 movement distance.Except for fingerIO that uses OFDM phase [5]. second shown in Figure 3(b).This is equivalent to hand movement no prior work has used phase changes of sound signals to measure distance of 4.04 cm considering the two-way path length change movement distance,although the phase of RF baseband signal has Furthermore.we can determine whether the hand is moving toward been used for measuring the movement distance of objects [2,23] or moving away from the microphone by the sign of the phase Compared to the Doppler shift,the phase change of the baseband changes.Note that it is important to use both the I and Q com- signal can be easily measured in the time domain.Figure 3 shows ponents because the movement direction information is lost when the In-phase (I)and the Quadrature (Q)components of the base- we only use a single component or the magnitude [23]. band signal obtained from the same sound record that produces the This phase based distance measurement approach has three ad- spectrogram in Figure 2.From Figure 3(a).we observe that the I/O vantages over the Doppler shift based approach.First,the accuracy waveforms remain static when the hand is not moving and vary like is much higher because by directly measuring the phase changes sinusoids when the hand moves.Combining the in-phase (as the we eliminate the noise-prone steps of first measuring the Dop- real part)and quadrature (as the imaginary part)components into pler shift and then integrating the Doppler shift to get the dis a complex signal,we can clearly observe patterns caused by hand tance changes.Second,the latency is much lower because the phase movement.Figure 3(b)shows how the complex signal changes dur- measurement can be conducted on a short data segment with only ing a short time period from 4.04 to 4.64 seconds while the hand hundreds of samples.Third,the speed resolution is much higher moves towards the microphone.We observe that the traces of the because the phase measurement can track small phase changes complex signal are close to circles on the complex plane. and slow phase shifts.For example,phase based measurement can In essence,the complex signal is a combination of two vectors easily achieve 2.4 mm distance resolution,which corresponds to in the complex plane:we call a static vector and a dynamic vector. a phase change of /4 when the wavelength is 1.9 cm.Further- The static vector corresponds to the sound wave traveling through more,the information is much richer because phase measurements the LOS path or reflected by static objects,such as walls and tables. provide more information than what we get from STFT.For ex- This vector remains quasi-static during this short time period.The ample,the phase difference at different frequencies can be used for dynamic vector corresponds to the reflection caused by the moving localizing the hand as discussed in Section 4 hand.When the hand moves towards the microphone,we observe an increase in the phase of the dynamic vector,which is caused 3.3 LLAP Overview by the decrease in length of the reflected path.As the phase of We now give an overview of LLAP when operating on a single the signal increases by 2 when the path length decreases by one sound frequency.Without loss of generality,we assume that the wavelength of the sound wave,we can calculate the distance that sampling frequency of the device is 48 kHz.We have tested our the hand moves via the phase change of the dynamic vector.As- implementation under other sampling frequencies,e.g.,44.1 kHzFigure 2: Doppler shift of hand movements however, the frequency with the highest energy, which is plotted as the white line around 18 kHz in Figure 2, does not closely fol￾low the hand movement because the sound waves reflected by the moving hand are mixed with the sound waves traveling through the Line-Of-Sight (LOS) path as well as those reflected by static ob￾jects. Furthermore, there are impluses in the Doppler shift measure￾ments due to frequency selective fading caused by the hand move￾ment, i.e., the sound waves traveling from different paths may get cancelled with each other on the target frequency when the hand is at certain positions. 3.2 Phase Based Distance Measurement Because of the above limitations of Doppler shift based distance measurement, we propose a phase based distance measurement ap￾proach for sound signals. As Doppler shift in the reflected signal is caused by the increase/decrease in the phase of the signal when the hand moves close/moves away, the idea is to treat the reflected signal as a phase modulated signal whose phase changes with the movement distance. Except for fingerIO that uses OFDM phase [5], no prior work has used phase changes of sound signals to measure movement distance, although the phase of RF baseband signal has been used for measuring the movement distance of objects [2, 23]. Compared to the Doppler shift, the phase change of the baseband signal can be easily measured in the time domain. Figure 3 shows the In-phase (I) and the Quadrature (Q) components of the base￾band signal obtained from the same sound record that produces the spectrogram in Figure 2. From Figure 3(a), we observe that the I/Q waveforms remain static when the hand is not moving and vary like sinusoids when the hand moves. Combining the in-phase (as the real part) and quadrature (as the imaginary part) components into a complex signal, we can clearly observe patterns caused by hand movement. Figure 3(b) shows how the complex signal changes dur￾ing a short time period from 4.04 to 4.64 seconds while the hand moves towards the microphone. We observe that the traces of the complex signal are close to circles on the complex plane. In essence, the complex signal is a combination of two vectors in the complex plane: we call a static vector and a dynamic vector. The static vector corresponds to the sound wave traveling through the LOS path or reflected by static objects, such as walls and tables. This vector remains quasi-static during this short time period. The dynamic vector corresponds to the reflection caused by the moving hand. When the hand moves towards the microphone, we observe an increase in the phase of the dynamic vector, which is caused by the decrease in length of the reflected path. As the phase of the signal increases by 2π when the path length decreases by one wavelength of the sound wave, we can calculate the distance that the hand moves via the phase change of the dynamic vector. As- 3.5 4 4.5 5 5.5 6 6.5 7 7.5 8 −300 −200 −100 0 100 200 300 Time (seconds) I/Q (normalized) I Q (a) I/Q waveforms −200 −100 0 100 200 −300 −200 −100 0 100 I (normalized) Q (normalized) Starting (4.04s) Static vector Ending (4.64s) Dynamic vector (b) Complex I/Q traces Figure 3: Baseband signal of sound waves suming that the speed of sound is c = 343 m/s, the wavelength of sound signals with frequency f = 18 kHz is 1.9 cm. We observe that the complex signal moves by about 4.25 circles, which cor￾responds to an 8.5π increase in phase values in Figure 3(b). Thus, the path length changes by 1.9 × 4.25 = 8.08 cm during the 0.6 second shown in Figure 3(b). This is equivalent to hand movement distance of 4.04 cm considering the two-way path length change. Furthermore, we can determine whether the hand is moving toward or moving away from the microphone by the sign of the phase changes. Note that it is important to use both the I and Q com￾ponents because the movement direction information is lost when we only use a single component or the magnitude [23]. This phase based distance measurement approach has three ad￾vantages over the Doppler shift based approach. First, the accuracy is much higher because by directly measuring the phase changes, we eliminate the noise-prone steps of first measuring the Dop￾pler shift and then integrating the Doppler shift to get the dis￾tance changes. Second, the latency is much lower because the phase measurement can be conducted on a short data segment with only hundreds of samples. Third, the speed resolution is much higher because the phase measurement can track small phase changes and slow phase shifts. For example, phase based measurement can easily achieve 2.4 mm distance resolution, which corresponds to a phase change of π/4 when the wavelength is 1.9 cm. Further￾more, the information is much richer because phase measurements provide more information than what we get from STFT. For ex￾ample, the phase difference at different frequencies can be used for localizing the hand as discussed in Section 4. 3.3 LLAP Overview We now give an overview of LLAP when operating on a single sound frequency. Without loss of generality, we assume that the sampling frequency of the device is 48 kHz. We have tested our implementation under other sampling frequencies, e.g., 44.1 kHz