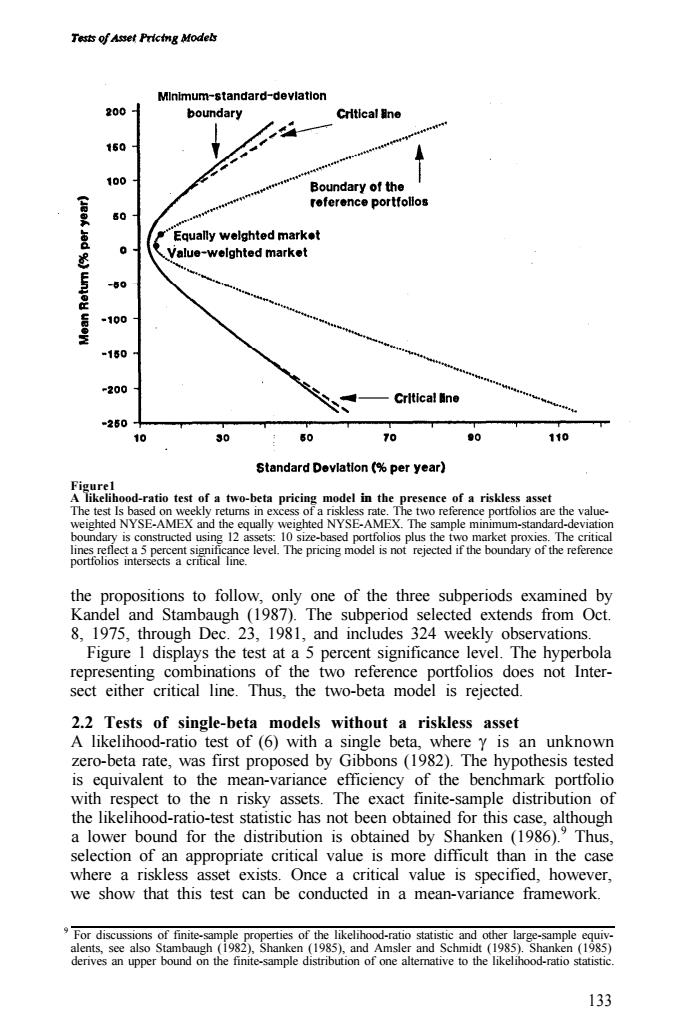
Tests of Asset Pricing Models MInimum-standard-devlation 200 boundary Critical ne t50 100 Boundary of the roference portfollos 60 Equally welghted market Q 0 Value-welghted market -50 -100 -150 -200 Crltical ne =250 10 30 60 70 90 110 Standard Devlation (per year) Figurel A likelihood-ratio test of a two-beta pricing model in the presence of a riskless asset The test Is based on weekly retums in excess of a riskless rate.The two reference portfolios are the value- weighted NYSE-AMEX and the equally weighted NYSE-AMEX.The sample minimum-standard-deviation boundary is constructed using 12 assets:10 size-based portfolios plus the two market proxies.The critical lines reflect a 5 percent significance level.The pricing model is not rejected if the boundary of the reference portfolios intersects a critical line. the propositions to follow,only one of the three subperiods examined by Kandel and Stambaugh (1987).The subperiod selected extends from Oct 8,1975,through Dec.23,1981,and includes 324 weekly observations. Figure 1 displays the test at a 5 percent significance level.The hyperbola representing combinations of the two reference portfolios does not Inter- sect either critical line.Thus,the two-beta model is rejected. 2.2 Tests of single-beta models without a riskless asset A likelihood-ratio test of (6)with a single beta,where y is an unknown zero-beta rate,was first proposed by Gibbons(1982).The hypothesis tested is equivalent to the mean-variance efficiency of the benchmark portfolio with respect to the n risky assets.The exact finite-sample distribution of the likelihood-ratio-test statistic has not been obtained for this case,although a lower bound for the distribution is obtained by Shanken (1986).Thus, selection of an appropriate critical value is more difficult than in the case where a riskless asset exists.Once a critical value is specified,however, we show that this test can be conducted in a mean-variance framework. For discussions of finite-sample properties of the likelihood-ratio statistic and other large-sample equiv- alents,see also Stambaugh(1982),Shanken (1985),and Amsler and Schmidt (1985).Shanken (1985) derives an upper bound on the finite-sample distribution of one altemative to the likelihood-ratio statistic. 133Figure1 A likelihood-ratio test of a two-beta pricing model in the presence of a riskless asset The test Is based on weekly returns in excess of a riskless rate. The two reference portfolios are the value￾weighted NYSE-AMEX and the equally weighted NYSE-AMEX. The sample minimum-standard-deviation boundary is constructed using 12 assets: 10 size-based portfolios plus the two market proxies. The critical lines reflect a 5 percent significance level. The pricing model is not rejected if the boundary of the reference portfolios intersects a critical line. the propositions to follow, only one of the three subperiods examined by Kandel and Stambaugh (1987). The subperiod selected extends from Oct. 8, 1975, through Dec. 23, 1981, and includes 324 weekly observations. Figure 1 displays the test at a 5 percent significance level. The hyperbola representing combinations of the two reference portfolios does not Inter￾sect either critical line. Thus, the two-beta model is rejected. 2.2 Tests of single-beta models without a riskless asset A likelihood-ratio test of (6) with a single beta, where g is an unknown zero-beta rate, was first proposed by Gibbons (1982). The hypothesis tested is equivalent to the mean-variance efficiency of the benchmark portfolio with respect to the n risky assets. The exact finite-sample distribution of the likelihood-ratio-test statistic has not been obtained for this case, although a lower bound for the distribution is obtained by Shanken (1986).9 Thus, selection of an appropriate critical value is more difficult than in the case where a riskless asset exists. Once a critical value is specified, however, we show that this test can be conducted in a mean-variance framework. 9 For discussions of finite-sample properties of the likelihood-ratio statistic and other large-sample equiv￾alents, see also Stambaugh (1982), Shanken (1985), and Amsler and Schmidt (1985). Shanken (1985) derives an upper bound on the finite-sample distribution of one alternative to the likelihood-ratio statistic. 133