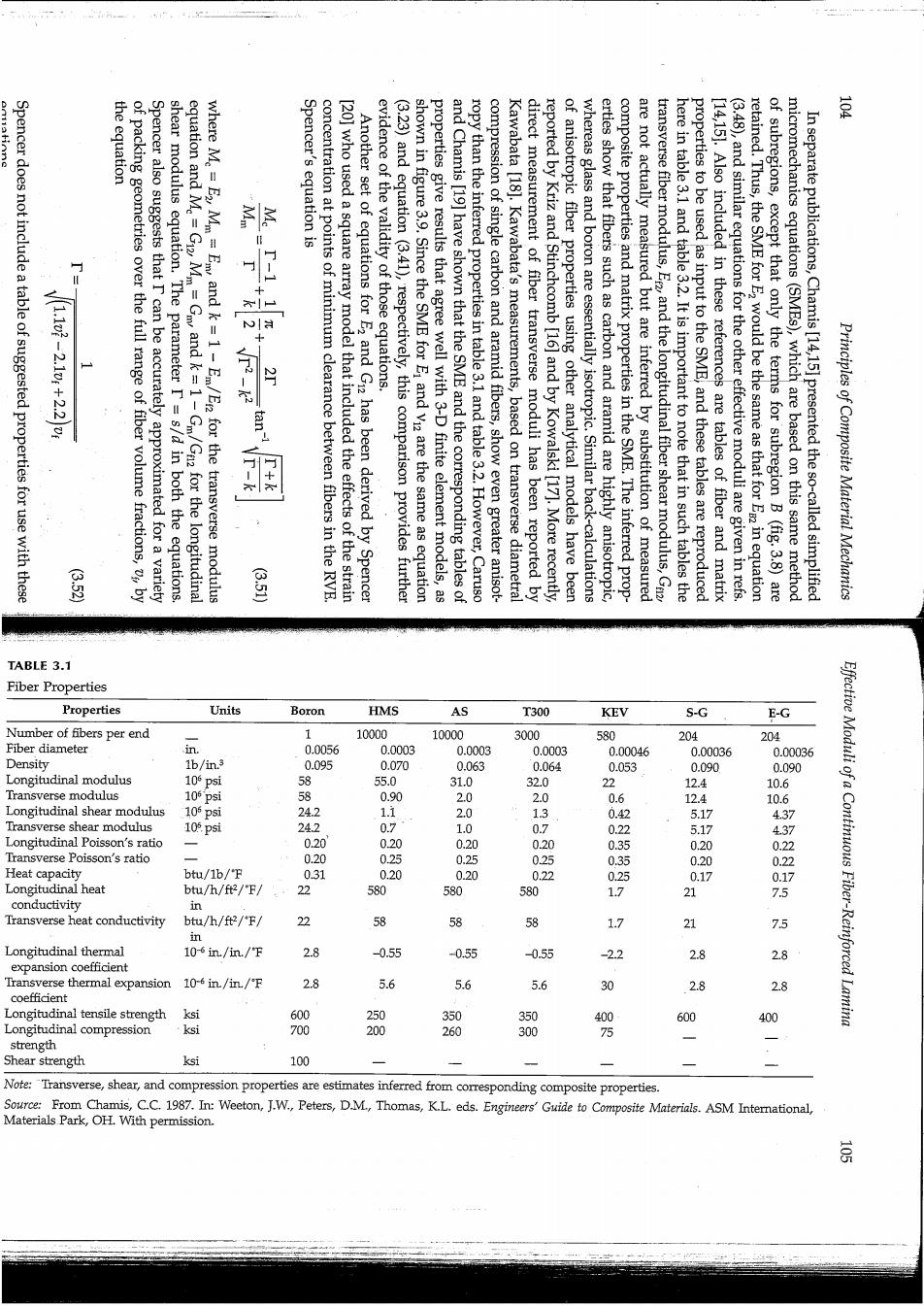
0119E the equation Spencer Spencer does not include a table of suggested properties for use with of packing geometries over Mm equation is 1100-210422/ the full range of fiber volume fractions,v,by Spencer also suggests that I can be accurately approximated for a variety shear modulus equation.The parameter I=s/d in both the equations. equation and M=G12,Mm=Gm,and k=1-Gm/Gn2 for the longitudinal where M=E2,Mm =Em,and k=1-Em/Er2 for the transverse modulus concentration at points of minimum clearance between fibers in the RVB [20]who used a square array model that included the effects of the strain Another set of equations for E2 and Gi2 has been derived by Spencer evidence of the validity of those equations. (3.23)and equation (3.41),respectively,this comparison provides further shown in figure 3.9.Since the SME for Ei and vi are the same as equation properties give results that agree well with 3-D finite element models,as and Chamis [19]have shown that the SME and the corresponding tables of ropy than the inferred properties in table 3.1 and table 3.2.However,Caruso compression of single carbon and aramid fibers,show even greater anisot- Kawabata [18].Kawabata's measurements,based on transverse diametral direct measurement of fiber transverse moduli has been reported by reported by Kriz and Stinchcomb [16]and by Kowalski [17].More recently, of anisotropic fiber properties using other analytical models have been whereas glass and boron are essentially isotropic.Similar back-calculations erties show that fibers such as carbon and aramid are highly anisotropic, composite properties and matrix properties in the SME.The inferred prop- are not actually measured but are inferred by substitution of measured transverse fiber modulus,E2 and the longitudinal fiber shear modulus,Ga2 here in table 3.1 and table3.2.It is important to note that in such tables the properties to be used as input to the SME,and these tables are reproduced [14,15].Also included in these references are tables of fiber and matrix (3.48),and similar equations for the other effective moduli are given in refs. retained.Thus,the SME for E2 would be the same as that for E2 in equation of subregions,except that only the terms for subregion B (fig.3.8)are micromechanics equations(SMEs),which are based on this same method In separate publications,Chamis[14,15]presented the so-called simplified Principles of Composite Material Mechanics these TABLE 3.1 Fiber Properties Properties Units Boron HMS AS T300 KEV S-G E-G Number of fibers per end 10000 10000 3000 580 204 204 Fiber diameter 0.0056 0.0003 0.0003 0.0003 0.00046 0.00036 0.00036 Density 1b/in.3 0.095 0.070 0.063 0.064 0.053 0.090 0.090 Effective Moduli of a Longitudinal modulus 105 psi 55.0 31.0 32.0 22 12.4 10.6 Transverse modulus 58 0.90 2.0 2.0 0.6 12.4 10.6 Longitudinal shear modulus 105 psi 24.2 1.1 2.0 13 0.42 5.17 4.37 Transverse shear modulus 105psi 24.2 0.7 1.0 0.7 0.22 5.17 4.37 Longitudinal Poisson's ratio 0.20 0.20 0.20 020 836 0.20 0.22 Transverse Poisson's ratio 0.20 0.25 0.25 025 0.20 Heat capacity btu/1b/℉ 0.31 0.20 0.20 0.22 0.25 0.22 0.17 Longitudinal heat btu/h/ft2/℉ 22 580 580 580 1.7 3 9阳 conductivity in Transverse heat conductivity btu/h/ft2/℉/ 22 58 58 58 1.7 少 7.5 n Longitudinal thermal 106in./in./℉ 2.8 0.55 -0.55 -0.55 -22 2.8 2.8 expansion coefficient Transverse thermal expansion 106in/in./℉ 2.8 5.6 Continuous Fiber-Reinforced Lamina 5.6 5.6 30 2.8 2.8 coefficient Longitudinal tensile strength ksi 600 250 350 350 400 600 400 Longitudinal compression ksi 700 200 260 300 75 strength Shear strength ksi 100 Note:Transverse,shear,and compression properties are estimates inferred from corresponding composite properties. Source:From Chamis,C.C.1987.In:Weeton,J.W.,Peters,D.M,Thomas, K.L eds Engineers Guide to Composite Materials. ASM International, Materials Park,OH.With permission